Реферат на тему
«Математика в физическом спорте»
Оглавление
Введение
Основы теории спортивных измерений
Характеристика спортивных измерений
Единицы измерений
Шкалы измерений
Точность измерений
Математические методы в спорте
Функциональная зависимость
Биомеханическая модель
Методы Декарта
3. Математический расчет в тренировочном процессе
3.1. Расчет нагрузки и питания
3.2. Арифметика тенниса
3.3. Регистрация достижений
4. Прикладные задачи, используемые в практике обучения «Физической культуры»
Выводы
Список используемой литературы
Введение
Тренер — инженер-наладчик, помогающий спортсмену в саморазвитии задатков-способностей, которые заложены в человеческом теле и востребованы определенным видом спорта, доводя их до ярко выраженного индивидуального уровня. Эта работа относится к области сложного для понимания человеком природного механизма — человеческого тела, поэтому профессия требует от тренера самых обобщенных определенных знаний о природных явлениях.
Так как в спорте присутствует и порядок, и мера, математика для него не может быть сторонней наукой.
Ценность математики в том, что она содержит укрупненные единицы информации, которые развивают человека разумного в еще более разумного — в индивидуально мыслящую личность с индивидуальными особенностями поведения.
Например, «Спортивная метрология» как учебная дисциплина осуществляет свою деятельность в образовательной области по физической культуре и спорту. Содержание спортивной метрологии определено следующими направлениями: выразить числом явления и процессы, которые происходят в физической культуре и спорте, используя конкретные современные способы измерения, и обработать полученный материал методами математической статистики. Ведь численная мера позволяет выявить тенденции и закономерности, определить базовые понятия в науке и спорте.
Цель работы – исследование направлений применения прикладной математики в физической культуре и спорте.
Прикладная математика — область математики, применяющая математические методы в других областях науки и практики: биоматематика и биоинформатика, теория информации, теория игр, теория вероятностей и статистика, финансовая математика и теория страхования, криптография и многое другое.
Математические методы достаточно широко применяются в области накопления информации (это называется статистика) и обработки данных, в самых разнообразных сферах, в том числе в физической культуре и спорте.
1.Основы теории спортивных измерений
1.1. Характеристика спортивных измерений
Измерение какой-либо физической величины — операция, в результате которой определяется, во сколько раз эта величина больше (или меньше) другой величины, принятой за эталон, или (в широком смысле слова) установление соответствия между изучаемыми явлениями, с одной стороны, и числами, с другой.
Эталон — это высокоточная мера, предназначенная для воспроизведения и хранения единицы величины с целью передачи ее размера другим средствам измерений, выполненная по особой спецификации и официально утвержденная в установленном порядке в качестве эталона. От эталона единица величины передается разрядным эталонам, а от них — рабочим средствам измерений.
Так, за эталон длины принят метр. Проводя измерения в со-ревнованиях или в тесте, мы узнаем, сколько метров, например, содержится в результате, показанном спортсменом, в прыжке в длину, в толкании ядра и т.д. Точно так же можно измерить вре-мя движений, мощность, развиваемую при их выполнении, и т.п.
1.2. Единицы измерений
Измерение физической величины можно проводить прямым или косвенным методами. При прямом методе измерения физическая величина определяется опытным путем (например, длина дистанции, время и т.д.). При косвенном методе измерения физи-ческая величина вычисляется на основании известной зависимости физических величин друг от друга, полученных опытным путем (например, определение величины средней скорости спортсмена от длины дистанции и времени забега и т.д.).
| Международная система единиц (СИ) Величина | Обозначение |
| наименование | русское | международное |
| Основные единицы измерений |
| Длина, l | метр | м | m |
| Масса, m | килограмм | кг | kg |
| Время, t | секунда | с | s |
| Сила электрического тока, I | ампер | А | A |
| Термодинамическая температура, T, | кельвин | К | K |
| Сила света, J | кандела | кд | cd |
| Количество вещества, n | моль | моль | mol |
1.3. Шкалы измерений
Проведение любых исследований, в том числе и в области физического воспитания и спорта, связано с определенными измерениями. Измерение в самом широком смысле может быть определено как приписывание чисел к объектам или событиям согласно некоторым правилам. Эти правила должны устанавливать соответствие между свойствами рассматриваемых объектов и чисел, что порождает четыре основных вида таких шкал: наименований, порядка, интервальная и отношений. Измерения, осуществляемые с помощью двух первых шкал, считаются качественными, двух последних — количественными. В каждой шкале строго определены свойства чисел. При этом чем выше порядок шкалы, тем больше арифметических действий разрешается проводить над числами, приписанными объектам.
Шкала наименований (номинальная шкала)
Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов (например, нумерация игроков футбольной команды). Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше — меньше», поэтому некоторые полагают, что применение шкалы наименований не следует считать измерением. Построение этой шкалы основано на группировке объектов, явлений в соответствующие классы в зависимости от проявления у них определенных признаков или свойств. Всем объектам или явлениям, попавшим в один и тот же класс, группу, приписывается одно и то же число, объектам и явлениям другого класса — другое число. Например, всех студентов факультета в зависимости от того, в каком виде спорта они специализируются, можно подразделить на следующие классы: баскетболисты, волейболисты, гимнасты, футболисты, лыжники, легкоатлеты и т.д. В данном случае классу баскетболистов можно приписать цифру 1; волейболистов — 2; гимнастов — 3; футболистов — 4; лыжников — 5; легкоатлетов — 6 и т.д. В результате все студенты факультета будут отнесены к тому или иному классу, группе специализаций. Таким же образом можно подразделить студентов или других занимающихся на определенные классы в зависимости от пола, возраста, разряда, принадлежности к тому или иному спортивному клубу и т.д.
При использовании шкалы наименований могут проводиться только некоторые математические операции. Например, ее числа нельзя складывать или вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка
Порядковые измерения (ранжирование) возможны тогда, когда исследователь может обнаружить в объектах или явлениях различие степеней признака или свойства и на этой основе расположить эти объекты в порядке возрастания или убывания величины рассматриваемого признака. Каждому объекту или явлению в этом случае приписывается порядковое число, обозначающее его место в данном ряду. Это число называют рангом.
Ранговые числа подбираются так, чтобы объектам с большей величиной изучаемого признака приписывались числа бóльшие, чем у объектов с меньшей величиной этого признака.
Примерами измерения на основе шкалы порядка могут служить распределение студентов факультета в зависимости от того или иного спортивного разряда по возрастающему порядку — от III разря-да до звания мастера спорта. В практике измерений результатов учебно-тренировочного процесса шкалу порядка можно использовать всякий раз, когда имеется критерий, позволяющий расположить занимающихся или явление по степени увеличения или уменьшения измеряемого признака. Следовательно, эту шкалу целесообразно применять в тех случаях, когда нужно определить характер неравенства в виде суждений: «выше — ниже», «больше — меньше», «лучше — хуже» и т.д., и невозможно при этом измерить величину этой разницы.
1.4. Точность измерений
Основные понятия
В спортивной практике наибольшее распространение получили два вида измерений. Измерения, когда искомое значение величины находится непосредственно из опытных данных, являются прямыми, например, регистрация скорости бега, дальности метания, величины усилий и т.п.
Косвенными называют измерения, при которых искомое значение величины находят на основании зависимости между этой величиной и величинами, подвергаемыми измерению. Например, между скоростью ведения мяча футболистом (V) и затратами энергии (Е) существует зависимость типа:
У = 1,683 + 1,322 × Х,
где У — затраты энергии в ккал; Х — скорость ведения мяча.
Если спортсмен ведет мяч с V = 6 м/с, то Е = 9,6 ккал/мин.
Прямым способом, например, измерить МПК сложно, а время бега — легко, поэтому время бега измеряют, а МПК — рассчитывают.
Следует помнить, что никакое измерение не может быть выполнено абсолютно точно, и результат измерения всегда содержит в себе ошибку. Необходимо стремиться к тому, чтобы эта ошибка была разумно минимальна. Напомним, что результаты контроля являются основой для планирования нагрузок: если точно измерили показатели, то и точно спланировали дальнейшую физическую нагрузку и наоборот. Знание точности измерений — обязательное условие, поэтому в задачу измерений входит не только нахождение самой величины, но и оценка допущенных при этом погрешностей (ошибок).
Систематические и случайные ошибки измерений
Ошибки измерений подразделяются на систематические и случайные.
Абсолютные и относительные ошибки измерений
Как было сказано выше, результат измерения любой величины отличается от истинного значения. Это отличие, равное разности между показанием прибора и истинным значением, называется абсолютной погрешностью измерения, которая выражается в тех же единицах, что и сама измеряемая величина:
А = А – Ао,
где А — абсолютная погрешность; А — показатель прибора; Ао — истинное значение.
Действительная относительная погрешность определяется как отношение абсолютной погрешности к истинным значениям измеряемой величины.
При проведении комплексного контроля, когда измеряются показатели разной размерности, целесообразнее пользоваться не абсолютной, а относительной погрешностью. Она определяется как отношение абсолютной погрешности к максимально возможному значению измеряемой величины.
В тех случаях, когда оценивается не погрешность самого измерения, а погрешность измерительного прибора, за максимальное значение измеряемой величины принимают предельное значение шкалы прибора. При таких расчетах полученное значение, выраженное в процентах, определяет класс точности прибора в нормальных условиях работы.
2.Математические методы в спорте
2.1. Функциональная зависимость
Так как в спорте присутствует и порядок, и мера, математика для него не может быть сторонней наукой.
Ценность математики в том, что она содержит укрупненные единицы информации, которые развивают человека разумного в еще более разумного - в индивидуально мыслящую личность с индивидуальными особенностями поведения.
Самой обобщенной и абстрактной единицей из укрупненных единиц познания и действия является метод (от греч .methodos: 1. Способ познания, исследования явлений природы и общественной жизни. 2. Прием, способ или образ действия. "Весь метод состоит в порядке и размещении того, на что должно быть направлено острие ума в целях открытия какой-либо истины".
Математика раскрывает метод как модель (от лат. modulus - мера, образец, схема, изображение или описание какого-либо предмета, явления или процесса в природе и обществе, изучаемые как аналог) познания порядка действия в самом общем и абстрактном виде, как единицу логического мышления, которая предшествует и сопутствует разумному, обдуманному, осознанному поведению индивида в среде.
А.Я. Хинчин (1977) считает, что "…ни одно из других понятий не отражает явлений реальной действительности с такой непосредственностью и с такой конкретностью, как понятие функциональной зависимости, в которой воплощены и подвижность, и динамичность реального мира, и взаимная обусловленность реальных величин".
Функция, функциональная зависимость - аналог, модель ситуации в виде, отражающем отношения между характерными параметрами, с выделением аргумента или аргументов (от лат. argumentum - довод, основание) - основных управляющих элементов ситуации.
Модель процесса в основных элементах:

Смысл "ключевого" математического слова функция (от лат. funktio -исполнение) трактуется как: 1. Деятельность, обязанность, работа, внешнее проявление свойств какого-либо объекта в данной системе отношений; 2. Мат. зависимая (следствие) переменная величина, т.е. величина, изменяющаяся по мере изменения другой (независимой - причине) величины, называемой аргументом .
Что дает это самое общее и самое абстрактное знание тренеру, как его можно использовать?
Зона мышления определяется приватным предметом как процессом и может представлять любую область человеческих потребностей.
Всякий процесс (последовательность, порядок, на практике - ответ на вопрос: это как?) имеет результат, итог тренировочного процесса - спортивный результат, желаемый или нет - это следующий вопрос.
Обычно результат - следствие определенных причин (аргументов). Спортивный тренинг - развитие аргументов, которые определяют спортивный результат. Причем если результат очевиден, то причина или причины могут быть далеко не очевидными.
Процесс развивается соответственно изменению меры (мера - одна из важнейших философских категорий, выражающая единство качества и количества, на практике ответ на вопрос: это что и этого сколько?) аргумента или аргументов.
В случае верного выбора меры аргумента или аргументов результат будет близок к желаемому.
Возможны только две основных цели познания механизма действия:
анализировать: желаемый для спортсмена результат (функцию) исследовать, т.е. разложить на необходимые и достаточные элементы, выделив управляющие мерой результата условия (аргументы);
синтезировать: по известным аргументам проектировать, конструировать, реализовать спортивный процесс под определенный результат.
Следствием реализации вышеизложенных целей является аргументированное удовлетворение или аргументированная коррекция и корреляция желаемого результата через меры его аргументов.
Обратимся к ближайшей, более частной по отношению к математике, науке физике - обобщенному, но не абстрактному представлению об объективной реальности, предмет которой - тело как множество (масса) более мелких тел в объеме более крупного тела. Тело находится в процессе движения, что наиболее характерно для спорта:
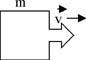
р = mv Озвучивает физик: тело, которое движется, может толкнуть или ударить другое тело; озвучивает математик: масса m и скорость v - вероятностные аргументы для функции - импульса силы p.
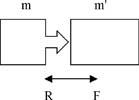
Озвучивает физик: в месте касания (контакта) одного тела с другим проявится реакция связи R (противодействие) на тело с массой m и действие F (сила) на второе тело с массой m',
где F = Dp/Dt.
Озвучивает математик: сила - функция, определенная аргументом - импульсом в единицу времени его действия.
F = m'a'. Озвучивает физик: сила F вызовет ускорение a' тела m', озвучивает математик: ускорение a' тела m' - функция аргумента F и т.д.
Что наблюдается? Физические законы - принципиальные модели качественно-количественных изменений, содержат функции и обобщенные вероятностные физические аргументы природных процессов.
Одному аргументу соответствует то же качество функции, и при наличии коэффициента - в другом количестве, а при большем количестве аргументов функция изменяет не только количество, но и качество.
2.2. Биомеханическая модель
Сопутствующие реальному процессу компоненты, элементы кинематических и трансмиссионных биомеханических структур могут, не изменяя качества, оказывать влияние на количество аргумента спортивного процесса, поэтому они должны учитываться в биомеханических моделях.
Биомеханическая модель - приближенная к реальности математическая модель - должна содержать в постоянных коэффициентах при физических аргументах те компоненты из индивидуальных природных компонентов, которые через аргумент влияют на количество результата процесса.
Не влияющие на меру физических аргументов, но влияющие на результат прочие виды вероятностных аргументов можно учесть в свободном члене математической модели.
Р. Декарт утверждал, что "... все доступное человеческому познанию одинаково вытекает одно из другого". Заметим, что каждый шаг физической последовательности сопровождается сменой ролей, создавая функциональный ряд, последовательность, функциональную цепь:
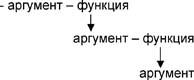
- и т.д., где функция одного порядка, безусловно, или при определенном условии, становится аргументом для функции следующего порядка.
2.3. Методы Декарта
И в заключение - четыре правила метода Декарта. Ими руководствовались авторы при написании данной статьи. Вчитайтесь - и вы узнаете принятую организацию тренировки по технике спорта.
"Второе - делить каждое из исследуемых затруднений на столько частей, сколько это возможно и нужно для лучшего их преодоления.
Третье - придерживаться определенного порядка мышления, начиная с предметов наиболее простых и наиболее легко познаваемых и восходя постепенно к познанию наиболее сложного, предполагая порядок даже и там, где объекты мышления вовсе не даны в их естественной связи.
И последнее: всегда составлять перечни столь полные и обзоры столь общие, чтобы была уверенность в отсутствии упущений.
Первое - никогда не принимать за истинное ничего, что не познал бы таковым с очевидностью, иначе говоря, тщательно избегать опрометчивости и предвзятости и включать в свои рассуждения только то, что представляется уму столь ясно и отчетливо, что не дает никакого повода подвергать их сомнению".
Первое правило указано последним только потому, что следствия (функции) для человека очевидны, а вот аргументы очевидны далеко не всегда, и знают об этом далеко не все тренеры, поэтому допускают серьезную ошибку, подменяя очевидной функцией неочевидный аргумент.
Ошибочно приняв за аргумент функцию, ее тренируют, считая причиной естественно недостаточного роста спортивного результата ограниченность способностей спортсмена.
Избежать этого тренеру позволят знания существенных для спорта функциональных цепей по всем видам аргументов.
Последнее утверждение и было поводом для написания статьи.
Математика - вершина натурфилософии - абстрактное обобщенное описание явлений объективной реальности, поэтому она не придаток, язык или средство, а именно источник всех других знаний, в том числе и связанных со спортом.
3.Математический расчет в тренировочном процессе
3.1. Расчет нагрузки и питания
При планировании тренировочного процесса, в обязательном порядке производится математический расчет различных видов тренировок. Не проводя математического моделирования той или иной тренировки, нельзя давать нагрузку спортсмену, так как в процессе учитываются: рост, вес, возраст, частота сердечных сокращений в минуту, показатели артериального давления, степень подготовленности спортсменов и многое другое. Только правильно спланированный и примененный тренировочный план не наносит вреда здоровью спортсмена и позволяет им приобрести хорошую физическую форму и добиться значимых спортивных результатов.
Если суточный рацион современного мужчины без активных физических нагрузок и без избыточного веса должен составлять ккал, для женщин ккал.
Дневной рацион спортсмена при длительной нагрузке должен включать в себя 5500–6500 ккал для мужчин и 5000–6000 ккал для женщин. Главное состоит в том, что с помощью привычных продуктов питания, даже обладающих высокой биологической ценностью, нет возможности компенсировать значительные (до 6 00ккал) суточные энергозатраты у спортсменов и связанный с ними расход пластических веществ.
Энергозатраты у спортсмена определяются еще большим числом составляющих:
— климато-географические условия тренировки,
— объем тренировки,
Компонентах пищи « разных видах спорта, среднесуточные
— интенсивность тренировки,
— вид спорта,
— частота тренировок,
— состояние при тренировке,
— специфическое динамическое действие пищи,
— температура тела спортсмена,
— профессиональная деятельность,
— пол,
— повышенный основной обмен,
— потери на пищеварение.
Усложняют расчет суточного рациона особые требования к водному и углеводному обмену (спортсмен не должен испытывать жажду и недостаток углеродов, как основных источников энергии).
При двухразовых тренировках распределение калорийности суточного рациона может быть следующим.
Первый завтрак...............5% Обед........................35%
Зарядка Полдник......................5%
Второй завтрак..............25% Дневная тренировка
Вечерняя тренировка Ужин.......................30%
При трехразовых тренировочных занятиях в день рекомендуется иной режим питания.
Первый завтрак.............. 15% Обед........................30%
Утренняя тренировка Полдник......................5%
Второй завтрак..............25% Вечерняя тренировка
Дневная тренировка Ужин.......................25%
Что интересно, существуют специальные программы-калькуляторы для расчета режима питания для различных видов спорта.
Вывод по разделу: расчет нагрузки тренировочного процесса и режима питания спортсменов основан на балансе энергозатрат и калорийности суточного рациона в ккал, рассчитывается исходя из множества исходных данных (вес, пол, длительность, интенсивность и частота тренировок, климатические условия), а также таблице калорийности продуктов.
3.2. Арифметика тенниса
Счет мячей в гейме имеет особенности, сохранившиеся с тех времен, когда игра велась на «интерес». Во Франции ценой игры являлась монета в 60су: она разменивалась на четыре по 15су. Эти последние и составляли цену четырех ударов: 15, 30, 45, 60. Правда, в ХХ веке судьи стали лаконичнее. Выкрикивая сорок вместо сорок пять.
Итак, при выигрыше первого в гейме мяча, счет становится 0:15 или 15:0. При выигрыше той же стороной второго мяча счет становится 30:0 или 0:30 в ее пользу. При выигрыше третьего мяча счет становится 40:0, при выигрыше четвертого 60:0 и приносит завершение гейма в пользу этой стороны.
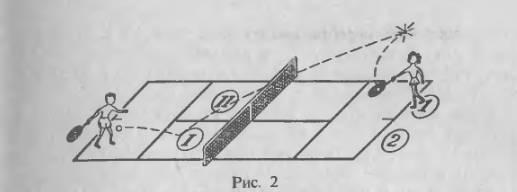
Если одна из сторон после выигрыша первого мяча второй мяч проиграла, то 15 засчитыается противнику и т. д. Следовательно, счет в гейме может быть одним из следующих: 15:0, 30:0, 40:0, 0:15, 0:30, 0:40, 15:15, 30:15, 40:15, 15:30, 15:40, 30:40, 30:30, ровно, больше, меньше, игра.
Счет «ровно» может быть при равенстве очков у противников начиная с шестого мяча, «больше»/»меньше» начиная с седьмого мяча, если подающий выиграл (проиграл) мяч после счета «ровно».
«Игра» подающего если при счете «больше» он выиграл следующий мяч, «игра» принимающего – когда при счете «меньше» подающий проиграл следующий мяч.
При завершении первого гейма, начинается второй гейм, подача переходит к противоположной стороне. Сет считается завершенным, если один из противников выиграл не менее шести геймов и получил перевес не менее чем на два гейма. Следовательно, сет заканчивается когда счет равен: 6:0, 6:1, 6:2, 6:3, 6:4, 7:5, 8:6 и т. д. По окончанию сета, разыгрывается второй сет, и т. д. до тех пор, пока одна из сторон не выиграет встречи двух (их трех) или трех (из пяти) в зависимости от условий соревнований. При выигрыше одной из сторон подряд двух сетов, ей присваивается победа и больше сетов не разыгрывается. Следовательно, счет встречи может быть 2:0, 2:1, или 3:2, 3:1 и т. д.
Таким образом, правила игры очень глубоко продуманы и ставят игроков в равные условия (выигрыш не менее чем в два мяча в гейме, два сета в игре), смена подач. Розыгрыш мяча имеет существенное, а иногда решающее значение для встречи, когда ход ее колеблется подобно весам. Именно поэтому возраст теннисисту не помеха, опыт позволяет более старшему игроку успешно противостоять более молодому, энергичному и выносливому.
3.3. Регистрация достижений.
Расстояние и время – важнейшие параметры в спорте при регистрации спортивных достижений (бег, плавание, всевозможные гонки и т. д.), в других видах спорта к ним добавляются поднятые килограммы, сложность и чистота исполнения акробатических элементов, выразительность. Следовательно, для определения победителя возникает необходимость количественного и качественного измерения результата.
На примере одного из наиболее престижных дисциплин «бег на 100 метров» можно наблюдать хронологию мировых рекордов и развития хронометража.
Бег на 100 метров и спортивный хронометраж
Фактор времени – важнейший в спорте. В одних видах состязаний просто идет сражение за время – бег в легкой атлетике, лыжные и лодочные гонки, конькобежный и велосипедный спорт, плавание и т. д. Но в беге на 100 м, прежде всего у мужчин, цена секунды, даже ее сотой доли, возрастает многократно. Обладатели рекордов в стометровке развивают максимально возможные для человека скорости и поэтому считаются самыми быстрыми людьми на планете. Ни один рекорд в легкой атлетике не приносит его автору столько славы, сколько лучший результат в коротком спринте.
Впервые электромеханическая система регистрации финиша появилась на Олимпийских играх в Стокгольме-1912, именно с этого года мировые рекорды на 100 м стали регистрироваться официально. Их список открыл Дональд Липпинкот (США) – 10,6 сек. Через девять лет на 0,2 сек. рекорд улучшил другойамериканец, Чарльз Пэддок – 10,4 сек. Прошло еще девять лет, и в 1930-м канадец Перси Уильямс сбросил с рекорда одну десятую – 10,3 сек. Напомним, что и Пэддок, и Уильямс становились олимпийскими чемпионами.
В 1928 году был создан ручной механический хронограф-секундомер, имеющий точность до одной сотой секунды. Первые камеры для фиксации финиша с такой точностью появились в 1930-м, они использовались на Олимпийских играх в Лос-Анджелесе-1932, официальным хронометражистом которых была фирма Omega. Победителя на 100 м определили по фотографиям – американцы Энди Тоулэн и Ральф Мэткалф показали одинаковое время – 10,38 сек.
На международных соревнованиях применяются современные стартовые колодки – довольно сложноеэлектронное устройство, передающее стартовый сигнал (его слышат все бегуны одновременно) и регистрирующее время старта с точностью до одной тысячной секунды.
Таким образом, человечество приближается к пределам своих скоростных возможностей, и развитие систем измерения оказываются напрямую связано с новыми мировыми достижениями.
Когда речь идет о сотых долях секунды, имеет значение любая мелочь: ветер, одежда и обувь спортсмена, подача стартового сигнала и многое другое. Кстати, 0,02 сек. соответствуют расстоянию 2 см (а 0,01 сек. – 1 см). Вспышка света такой продолжительности незаметна глазу человека.
Таким образом, даже направление и скорость ветра могут оказать существенное влияние на результат.
Скорость и реакция
Как уже говорилось, современные стартовые колодки фиксируют момент старта с точностью до 0,001 сек. Время прохождения стометровки настолько мало, что на результаты может влиять любая мелочь. Например, немаловажно, что при выстреле стартового пистолета старой модели звук быстрее достигает первой беговой дорожки, а до восьмой доходит в последнюю очередь. В зависимости от места нахождения судьи разница составляет от 0,025 до 0,052 сек., что при фиксации рекордов с точностью до 0,01 сек. весьма существенно.
Теперь же применяется стартовый пистолет японской конструкции Seiko, оснащенный так называемой системой электронного звука, она запускает отсчет времени одновременно со срабатыванием пистолета. Сигнал передается на колодки, снабженные динамиками, и все бегуны слышат хлопок одновременно. Наименьшее время реакции человека на звук (в том числе стартовый выстрел) считается равным 0,1 сек., более быстрый старт – это уже угадывание момента выстрела. Хотя данный вопрос до сих пор вызывает споры, движение с места раньше, чем на одну десятую секунды после выстрела, по правилам ИААФ, является фальстартом.
Выводы по разделу: во многих видах спорта, где требуется не только количественная, но и качественная оценка достижений (художественная и спортивная гимнастика, прыжки в воду, фигурное катание) итоговые результаты непосредственно связаны с математической обработкой данных. Да и количественная оценка проходит обязательную математическую обработку, с тем чтобы исключить неравенство спортсменов (скорость достижения сигнала старта) и влияние посторонних факторов (сила и направление ветра, температура воздуха и влажность).
4. Прикладные задачи, используемые в практике обучения «Физической культуры»
Важнейшим средством обучения математике в рамках профильного подхода к обучению, основанного на использовании метода математического моделирования – это прикладные, профессионально ориентированные задачи.
Прикладные, профессионально ориентированные задачи, привлекаемые в практику преподавания математики, должны удовлетворять следующим требованиям: демонстрировать приложение математического аппарата к практическим проблемам реальной жизни; способствовать отработке базовых математических знаний, умений и навыков; содействовать выработке профессионально значимых знаний, умений и навыков исходя из требований общенаучных, профессиональных и специальных дисциплин; нести смысловую нагрузку; обладать познавательной ценностью; выполнять функции воспитания и развития; быть доступными студентам по используемому в задаче нематематическому материалу; описывать реальную ситуацию; содержать не отвлеченные, а соответствующие действительности числовые значения величин; иметь практически приемлемое решение; иметь не очень громоздкое решение, чтобы не занимать много времени на занятии. Профессионально ориентированные задачи должны вырабатывать у студентов навыки и умения использования математического аппарата в практической жизни, способствовать созданию положительного эмоционального фона в процессе обучения, повышать интерес к изучению математики, формировать положительное отношение к выбранной профессии.
Опыт обучения математике с использованием профильного подхода показывает, что для повышения эффективности обучения необходимо иметь систему прикладных задач. Методическая система прикладных, профессионально ориентированных задач должна быть составлена следующим образом: используемые в практике преподавания задачи разбиты по разделам курса, что позволяет преподавателю готовить необходимый справочный материал и методические указания. Особую группу представляют прикладные,
профессионально ориентированные задачи, включаемые в индивидуальные
домашние задания.
Приведем примеры конкретных прикладных, профессионально
ориентированных задач, используемых в практике обучения студентов по
направлению «Физическая культура».
Задача 1. Группа школьников в течение летних каникул находилась в
спортивном лагере. До и после сезона измерена жизненная емкость легких (ЖЕЛ).
Значительно ли изменен этот показатель под влиянием интенсивных физических
нагрузок?
Значения показателя ЖЕЛ до эксперимента: 3 400, 3 600, 3 000, 3 500, 2 900,
3 100, 3 200, 3 400, 3 200, 3 400.
Значения ЖЕЛ после эксперимента: 3 800, 3 700, 3 300, 3 600, 3 100, 3 200,
3 200, 3 300, 3 500, 3 600.
Задача 2. Две группы юных баскетболистов в течение года тренировались по
разным программам. Эффективность нового цикла оценивалась по контрольному
упражнению – ведение мяча по прямой на отрезке 20 м на время. Результаты
выполнения упражнения (в сек.) следующие:
контрольная группа: 9,9; 9,7; 9,8; 10,3; 9,2; 9,0; 10,5; 10,1; 8,8; 9,5; 10,9; 9,8;
экспериментальная группа: 9,4; 9,6; 9,3; 9,1; 8,6; 9,0; 8,1; 9,6; 8,8; 9,3; 10,3; 9,9.
Можно ли утверждать, что вторая программа, по которой занималась
экспериментальная группа, более эффективна, чем первая?
Задача 3. Пусть за выполнение упражнения по гимнастике отмечены
результаты в баллах для спортсменов экспериментальной и контрольной групп:
экспериментальная группа: 7,9; 8,5; 9,0; 8,4; 9,2; 9,4; 9,1; 8,8; 8 1 n ;
контрольная группа: 7,8; 8,0; 8,2; 7,5; 8,4; 8,1; 8,6; 7 2 n .
Требуется проверить гипотезу о достоверности различий результатов в
группах.
Задача 4. Можно ли считать, что мнения трех судей, оценивавших
соревнования по фигурному катанию выступления мужчин в обязательном
упражнении, были согласованными. Результаты оценок представлены в таблице:
i N 1 2 3 4 5 6 7 8 9
i x 4,7 4,9 5,1 5,6 5,7 5,3 5,8 5,9 5,5
i y 4,3 4,5 5,3 5,2 5,4 5,5 5,9 5,6 5,7
i z 4,6 4,5 5,2 5,3 5,6 5,5 5,7 5,9 5,8
Задача 5.Студенты первого курса подвергнуты испытаниям в следующих
контрольных упражнениях: бег с ходу на дистанции 30 м (результат в секундах – x )
и тройном прыжке с места (результат в метрах – y ). Можно ли говорить о том, что
между результатами в беге на дистанции 30 м и результатами в тройном прыжке с
места существует сильная статистическая взаимосвязь? Результаты испытания
представлены в таблице:
i N 1 2 3 4 5 6 7 8 9 10
i x 3,5 3,6 3,6 3,6 3,8 3,7 3,9 3,4 3,6 3,6
i y 8,05 7,34 7,37 7,77 7,04 7,17 6,50 8,15 6,98 6,97
Задача 6. По данным задачи 5 результатов бега на дистанции 30 метров и
тройного прыжка с места построить линейные регрессионные модели y f (x) и
x f (y) . Какую из моделей использовать предпочтительнее?
На практических занятиях дополнительно к задачам из учебного пособия
предлагаются задачи, решаемые с помощью дисперсионного анализа. Например,
три группы юных баскетболистов в течение года тренировались по разным программам. Эффективность подготовки оценивалась по контрольному упражнению – ведение мяча по прямой на отрезке 20 м на время. Результаты выполнения упражнения (в сек.) следующие:
первая группа: 9,8; 9,6; 9,7; 10,2; 9,1; 8,9; 10,4; 10,0; 8,7; 9,4; 10,8; 9,7;
вторая группа: 9,3; 9,5; 9,2; 9,0; 8,5; 8,9; 8,0; 9,5; 8,7; 9,2; 10,2; 9,8;
третья группа: 9,6; 9,5; 9,4; 8,9; 9,1; 9,0; 8,6; 9,7; 10,0; 9,6; 10,3; 9,7.
Можно ли утверждать, что эффективность подготовки по этим программам в среднем одинакова (проверить гипотезу о равенстве групповых средних)?
Подобные задачи систематически используются нами на лекционных и практических занятиях, включаются в контрольные работы и индивидуальные домашние задания.
Рассмотренные методы и средства обучения математике позволяют реализовать воспитание через обучение, развить математическое мышление, способствуют профессиональной направленности личности будущих специалистов, их научного мировоззрения. Математическое моделирование позволяет реализовать принцип наглядности в обучении, повышает мотивацию обучения математике, вызывает устойчивый интерес как к математике, так и профессионально значимым дисциплинам, материал которых используется на занятиях по математике. Это способствует прочному усвоению и запоминанию учебного материала, возбуждает творческую работу мысли, имеет значение для реализации принципа сознательного, активного и самостоятельного усвоения знаний. Лучшей формой реализации принципа является самостоятельная работа студентов над индивидуальным заданием с профессиональным содержанием, в ходе которой они имеют возможность использовать приобретенные знания, навыки и умения, проявить творческий подход.
Выводы:
В результате своего исследования я пришел к следующим выводам:
1. Расчет нагрузки тренировочного процесса и режима питания спортсменов основан на балансе энергозатрат и калорийности суточного рациона в ккал, рассчитывается исходя из множества исходных данных (вес, пол, длительность, интенсивность и частота тренировок, климатические условия), а также таблице калорийности продуктов.
2. Во многих видах спорта, где требуется не только количественная, но и качественная оценка достижений (художественная и спортивная гимнастика, прыжки в воду, фигурное катание) итоговые результаты непосредственно связаны с математической обработкой данных. Да и количественная оценка проходит обязательную математическую обработку, с тем чтобы исключить неравенство спортсменов (скорость достижения сигнала старта) и влияние посторонних факторов (сила и направление ветра, температура воздуха и влажность).
3. Один из разделов математики теория вероятностей, а также статистика являются основными инструментами при прогнозировании мировых рекордов и расчете/оценке предельных значений мировых рекордов и человеческих возможностей.
5. С помощью метода математического моделирования можно предусмотреть тот или иной результат спортивного соревнования.
Математическое моделирование в рамках профильного подхода к обучению позволяет решить проблему формирования профессиональных компетенций выпускников направлений «Физическая культура».
Список используемой литературы
С.В. Начинская, Спортивная метрология: учебник для студентов учреждений высшего профессионального образования. - 4-е издание, стер., М.: Издательский центр «Академия» 2012.-240с.
Курс лекций по спортивной метрологии: Учебно-методическое пособие / Сост. О.С. Красникова.- Нижневартовск: Издательство Нижневарт. гос. ун-та, 2013.- 92.
Т.В. Васильева, И.Л. Елисеенко, Э.Р. Елисеенко, Роль и место методов математической статистики и моделирования в обучении студентов по направлениям «Физическая культура» и «Адаптивная физическая культура».
«Математика и спорт» Алексей Леонидович Садовский, Леонид Ефимович Садовский, М.:Наука, 1985. 192 с.Тираж 100000 экз.
Серия Библиотечка «Квант», выпуск 4.
Архив журнала «Наука и жизнь» №8 за 2007г «Бег на 100 метров и спортивный хронометраж» Кандидат технических наук Е. ГИК, кандидат биологических наук Е. ГУПАЛО.
Информация с сайта http://www. maa. org/pubs/Mathematics_and_Sports. html
http://lib.sportedu.ru
http://www. mathaware. org/mam/2010/



















