4
ВВЕДЕНИЕ
Цель работы: познакомится с таким статистическим методом, как дисперсионный анализ.
Дисперсионный анализ (от латинского dispersio – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике, медицине и др.
Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
При проведении исследования рынка часто встает вопрос о сопоставимости результатов. Например, проводя опросы по поводу потребления какого-либо товара в различных регионах страны, необходимо сделать выводы, на сколько данные опроса отличаются или не отличаются друг от друга. Сопоставлять отдельные показатели не имеет смысла и поэтому процедура сравнения и последующей оценки производится по некоторым усредненным значениям и отклонениям от этой усредненной оценки. Изучается вариация признака. За меру вариации может быть принята дисперсия. Дисперсия σ2 – мера вариации, определяемая как средняя из отклонений признака, возведенных в квадрат.
На практике часто возникают задачи более общего характера – задачи проверки существенности различий средних выборочных нескольких совокупностей. Например, требуется оценить влияние различного сырья на качество производимой продукции, решить задачу о влиянии количества удобрений на урожайность с/х продукции.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Дисперсионный анализ
В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель дисперсионного анализа с фиксированными уровнями факторов называют моделью I, модель со случайными факторами - моделью II. Благодаря варьированию фактора можно исследовать его влияние на величину отклика. В настоящее время общая теория дисперсионного анализа разработана для моделей I.
В зависимости от количества факторов, определяющих вариацию результативного признака, дисперсионный анализ подразделяют на однофакторный и многофакторный.
Основными схемами организации исходных данных с двумя и более факторами являются:
- перекрестная классификация, характерная для моделей I, в которых каждый уровень одного фактора сочетается при планировании эксперимента с каждой градацией другого фактора;
- иерархическая (гнездовая) классификация, характерная для модели II, в которой каждому случайному, наудачу выбранному значению одного фактора соответствует свое подмножество значений второго фактора.
Если одновременно исследуется зависимость отклика от качественных и количественных факторов, т.е. факторов смешанной природы, то используется ковариационный анализ.
При обработке данных эксперимента наиболее разработанными и поэтому распространенными считаются две модели. Их различие обусловлено спецификой планирования самого эксперимента. В модели дисперсионного анализа с фиксированными эффектами исследователь намеренно устанавливает строго определенные уровни изучаемого фактора. Термин «фиксированный эффект» в данном контексте имеет тот смысл, что самим исследователем фиксируется количество уровней фактора и различия между ними. При повторении эксперимента он или другой исследователь выберет те же самые уровни фактора. В модели со случайными эффектами уровни значения фактора выбираются исследователем случайно из широкого диапазона значений фактора, и при повторных экспериментах, естественно, этот диапазон будет другим.
Таким образом, данные модели отличаются между собой способом выбора уровней фактора, что, очевидно, в первую очередь влияет на возможность обобщения полученных экспериментальных результатов. Для дисперсионного анализа однофакторных экспериментов различие этих двух моделей не столь существенно, однако в многофакторном дисперсионном анализе оно может оказаться весьма важным.
При проведении дисперсионного анализа должны выполняться следующие статистические допущения: независимо от уровня фактора величины отклика имеют нормальный (Гауссовский) закон распределения и одинаковую дисперсию. Такое равенство дисперсий называется гомогенностью. Таким образом, изменение способа обработки сказывается лишь на положении случайной величины отклика, которое характеризуется средним значением или медианой. Поэтому все наблюдения отклика принадлежат сдвиговому семейству нормальных распределений.
В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия σ2. Она является мерой вариации частных средних по группам  вокруг общей средней
вокруг общей средней  и определяется по формуле:
и определяется по формуле:
 ,
,
где k - число групп;
nj - число единиц в j-ой группе;
 - частная средняя по j-ой группе;
- частная средняя по j-ой группе;
 - общая средняя по совокупности единиц.
- общая средняя по совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия σj 2.
 .
.
Между общей дисперсией σ0 2, внутригрупповой дисперсией σ2 и межгрупповой дисперсией  существует соотношение:
существует соотношение:
σ0 2 =  + σ2.
+ σ2.
Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе.
Однофакторный дисперсионный анализ
Однофакторная дисперсионная модель имеет вид:
xij = μ + Fj + εij , (1)
где хij – значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,...,т) c j-м порядковым номером (j=1,2,...,n);
Fi – эффект, обусловленный влиянием i-го уровня фактора;
εij – случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня.
Основные предпосылки дисперсионного анализа:
- математическое ожидание возмущения εij равно нулю для любых i, т.е.
M(εij ) = 0; (2)
- возмущения εij взаимно независимы;
- дисперсия переменной xij (или возмущения εij ) постоянна для
любых i, j, т.е.
D(εij ) = σ2 ; (3)
- переменная xij (или возмущение εij ) имеет нормальный закон
распределения N(0;σ2 ).
Влияние уровней фактора может быть как фиксированным или систематическим (модель I), так и случайным (модель II).
Пусть, например, необходимо выяснить, имеются ли существенные различия между партиями изделий по некоторому показателю качества, т.е. проверить влияние на качество одного фактора - партии изделий. Если включить в исследование все партии сырья, то влияние уровня такого фактора систематическое (модель I), а полученные выводы применимы только к тем отдельным партиям, которые привлекались при исследовании. Если же включить только отобранную случайно часть партий, то влияние фактора случайное (модель II). В многофакторных комплексах возможна смешанная модель III, в которой одни факторы имеют случайные уровни, а другие – фиксированные.
В таблице 1.1 представлен общий вид вычисления значений, с помощью дисперсионного анализа.
Таблица 1.1 – Базовая таблица дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат | Математическое ожидание среднего квадрата |
| Межгрупповая | 
| m-1 |  = Q1 /(m-1) = Q1 /(m-1)
| 
|
| Внутригрупповая | 
| mn-m |  = Q2 /(mn-m) = Q2 /(mn-m)
| M(S )= σ2 )= σ2 |
| Общая | 
| mn-1 |
|
|
Общая факторная и остаточная суммы квадратов отклонений
Пусть на количественный нормально распределенный признак X воздействует фактор  , который имеет
, который имеет  постоянных уровней. Будем предполагать, что число наблюдений (испытаний) на каждом уровне одинаково и равно
постоянных уровней. Будем предполагать, что число наблюдений (испытаний) на каждом уровне одинаково и равно  .
.
Пусть наблюдалось  значений
значений  признака X, где
признака X, где  – номер испытания
– номер испытания  ,
,  – номер уровня фактора
– номер уровня фактора 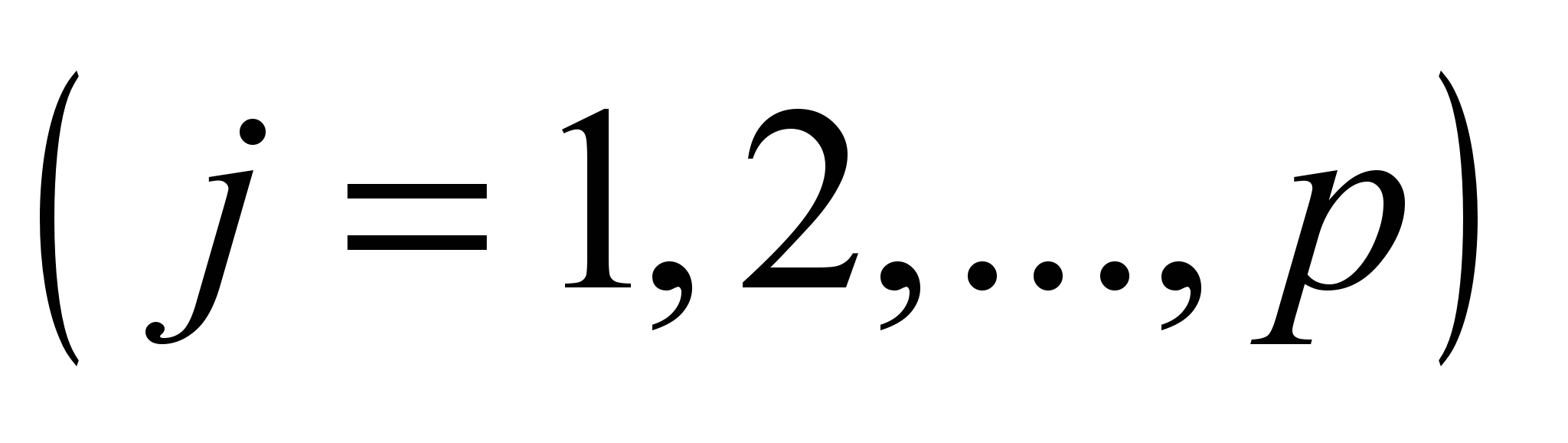 .
.
Введем, по определению:
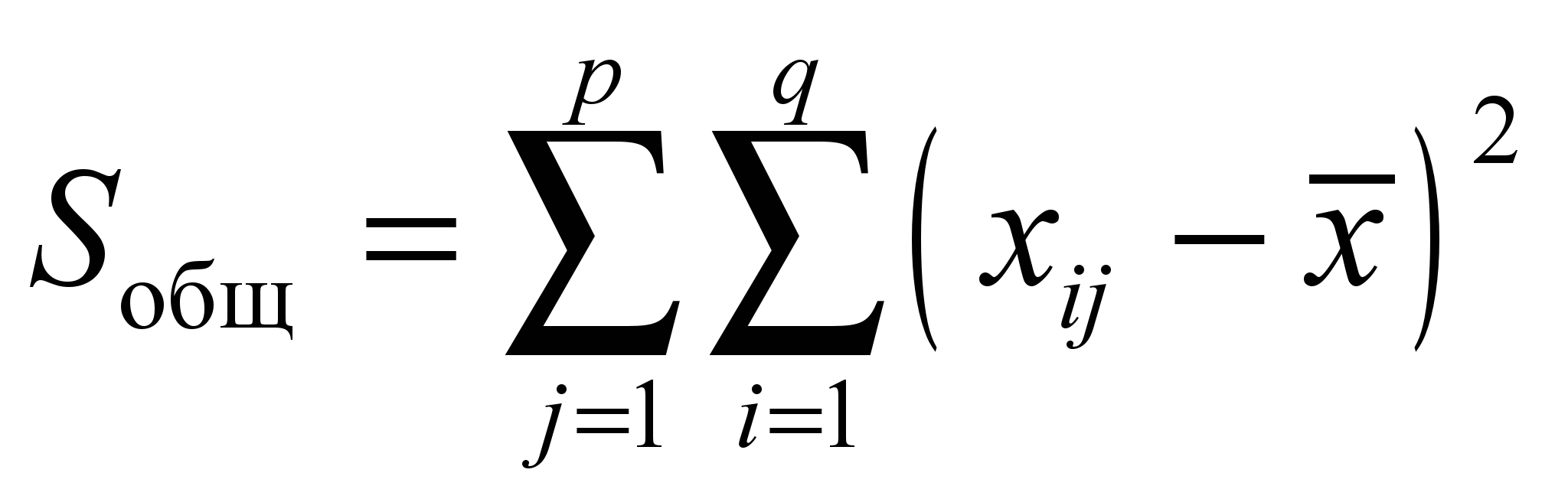 (общая сумма квадратов отклонений наблюдаемых значений от общей средней );
(общая сумма квадратов отклонений наблюдаемых значений от общей средней );
(факторная сумма квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние “между группами”);
(остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние “внутри групп”).
Практически остаточную сумму находят по равенству .
Элементарными преобразованиями можно получить формулы, более удобные для расчетов:
, ,
где – сумма квадратов значений признака на уровне ; – сумма значений признака на уровне .
Убедимся, что характеризует воздействие фактора  . Допустим, что фактор оказывает существенное влияние на X. Тогда группа наблюдаемых значений признака на одном определенном уровне, вообще говоря, отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние, причем они тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. Отсюда следует, что для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних от общей средней (отклонение возводят в квадрат, чтобы исключить погашение положительных и отрицательных отклонений). Умножив эту сумму на
. Допустим, что фактор оказывает существенное влияние на X. Тогда группа наблюдаемых значений признака на одном определенном уровне, вообще говоря, отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние, причем они тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. Отсюда следует, что для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних от общей средней (отклонение возводят в квадрат, чтобы исключить погашение положительных и отрицательных отклонений). Умножив эту сумму на  , получим . Итак, характеризует воздействие фактора.
, получим . Итак, характеризует воздействие фактора.
2. Убедимся, что отражает влияние случайных причин. Казалось бы, наблюдения одной группы не должны различаться. Однако, поскольку на X, кроме фактора  , воздействуют и случайные причины наблюдения одной и той же группы, вообще говоря, различны и, значит, рассеяны вокруг своей групповой средней.
, воздействуют и случайные причины наблюдения одной и той же группы, вообще говоря, различны и, значит, рассеяны вокруг своей групповой средней.
Отсюда следует, что для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней, т. е. . Итак, характеризует воздействие случайных причин.
3. Убедимся, что отражает влияние и фактора и случайных причин. Будем рассматривать все наблюдения как единую совокупность. Наблюдаемые значения признака различны вследствие воздействия фактора и случайных причин. Для оценки этого воздействия целесообразно составить сумму квадратов отклонений наблюдаемых значений от общей средней, т. е. .
Итак, характеризует влияние фактора и случайных причин. Можно доказать, что .
Сравнение нескольких средних методом дисперсионного анализа
Вернемся к поставленной задаче: проверить при заданном уровне значимости нулевую гипотезу о равенстве нескольких средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями. Покажем, что решение этой задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера—Снедекора.
1. Пусть нулевая гипотеза о равенстве нескольких средних (далее будем называть их групповыми) правильна. В этом случае факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии и, следовательно, различаются незначимо. Если сравнить эти оценки по критерию  , то очевидно, критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.
, то очевидно, критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.
Таким образом, если гипотеза о равенстве групповых средних правильна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.
2. Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и отношение . В итоге окажется больше и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
Таким образом, если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.
Легко доказать от противного справедливость обратных утверждений: из правильности (ложности) гипотезы о дисперсиях следует правильность (ложность) гипотезы о средних.
Итак, для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию  нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа.
нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа.
Замечание 1. Если факторная дисперсия окажется меньше остаточной, то уже отсюда следует справедливость гипотезы о равенстве групповых средних и, значит, нет надобности прибегать к критерию  .
.
Замечание 2. Если нет уверенности в справедливости предположения о равенстве дисперсий рассматриваемых  совокупностей, то это предположение следует проверить предварительно, например по критерию Кочрена.
совокупностей, то это предположение следует проверить предварительно, например по критерию Кочрена.
Если число испытаний на каждом из уровней различны, а именно на , на , …, на , то используют следующие формулы:
,
где – сумма квадратов наблюдавшихся значений признака на уровне , – суммы наблюдавшихся значений признака на уровне 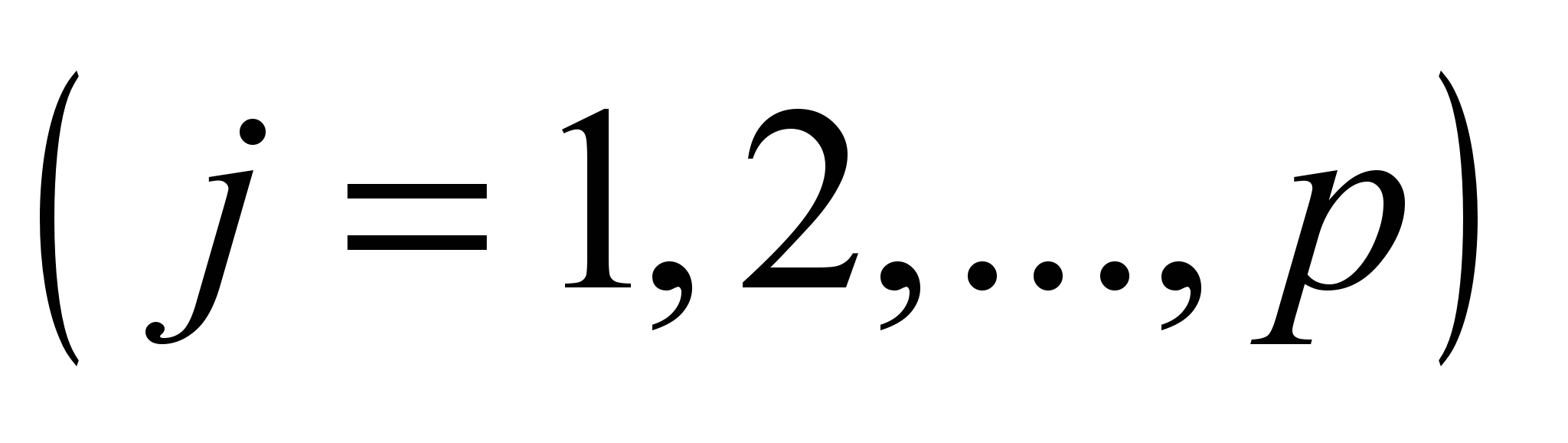 , – общее число испытаний (объем выборки).
, – общее число испытаний (объем выборки).
Двухфакторный дисперсионный анализ
В общем случае задача двухфакторного дисперсионного анализа формулируется следующим образом.
Имеются два фактора х1 и х2, каждый из которых имеет соответственно m1 и m2уровней. Для каждого из m1×m2 сочетаний уровней проводится n – одинаковое число наблюдений (в общем случае – разное), k = 1… n – номера наблюдений.
Общее число наблюдений N = m1×m2×n дают N значений наблюдаемой величины y ( ).
).
Например: х1 – наблюдатели, а i = 1…m1 – отдельные лица, обладающие различной квалификацией; х2 – приборы (j = 1…m2), обладающие различной точностью. По результатам наблюдений {yijk} требуется определить, что является причиной их отличия друг от друга – действие фактора х1(квалификация наблюдателя), фактора х2(различия в приборах), взаимное влияние факторов х1 и х2 или другие неучтенные факторы.
В соответствии с моделью двухфакторного анализа каждый результат наблюдения  можно представить в виде:
можно представить в виде:
 , где:
, где:
 - общее математическое ожидание наблюдаемой величины у;
- общее математическое ожидание наблюдаемой величины у;
 - эффект, обусловленный влиянием i-го уровня фактора х1;
- эффект, обусловленный влиянием i-го уровня фактора х1;
 - эффект, обусловленный взаимным влиянием j-го уровня фактора х2;
- эффект, обусловленный взаимным влиянием j-го уровня фактора х2;
 - эффект, обусловленный взаимным влиянием i-го уровня фактора х1 и j-го уровня фактора х2 (эффект взаимодействия);
- эффект, обусловленный взаимным влиянием i-го уровня фактора х1 и j-го уровня фактора х2 (эффект взаимодействия);
 - ошибка за счет влияния других неучтенных факторов.
- ошибка за счет влияния других неучтенных факторов.
Эффекты от соответствующих факторов или их взаимодействий определяются как:
 , i = 1…m1
, i = 1…m1
 , j = 1…m2
, j = 1…m2
,
i = 1…m1, j = 1…m2 
Здесь:
 - групповое математическое ожидание выходной переменной у на i-м уровне фактора х1 (в i-й группе);
- групповое математическое ожидание выходной переменной у на i-м уровне фактора х1 (в i-й группе);
 - групповое математическое ожидание выходной переменной у на j-м уровне фактора х2;
- групповое математическое ожидание выходной переменной у на j-м уровне фактора х2;
 - математическое ожидание выходной переменной у при фиксированных уровнях i и j факторов х1 и х2 соответственно;
- математическое ожидание выходной переменной у при фиксированных уровнях i и j факторов х1 и х2 соответственно;
 - математическое ожидание выходной переменной у в генеральной совокупности;
- математическое ожидание выходной переменной у в генеральной совокупности;
ошибка  - независимые случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием (me = 0) и дисперсией De = s2, одинаковой для всех i, j уровней факторов.
- независимые случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием (me = 0) и дисперсией De = s2, одинаковой для всех i, j уровней факторов.
Применения случайных процессов в экономике (в теории массового обслуживания)
Теория случайных процессов (случайных функций) – это раздел математической науки, изучающий закономерности случайных явлений в динамике их развития.
В настоящее время появилось большое количество литературы, посвященной непосредственно теории массового обслуживания, развитию ее математических аспектов, а также различных сфер ее приложения – военной, медицинской, транспортной, торговле, авиации и др.
Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого, варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и от простоев каналов обслуживания.
В коммерческой деятельности применение теории массового обслуживания пока не нашло желаемого распространения.
В основном это связано с трудностью постановки задач, необходимостью глубокого понимания содержания коммерческой деятельности, а также надежного и точного инструментария, позволяющего просчитывать в коммерческой деятельности различные варианты последствий управленческих решений.
Определение случайного процесса и его характеристики
Случайным процессом X(t) называется процесс, значение которого при любом значении аргумента t является случайной величиной.
Другими словами, случайный процесс представляет собой функцию, которая в результате испытания может принять тот или иной конкретный вид, неизвестный заранее. При фиксированном t = to X(to) представляет собой обычную случайную величину, т.е. сечение случайного процесса в момент tо.
Реализацией случайного процесса X (t, w) называется неслучайная функция x(t), в которую превращается случайный процесс X(t) в результате испытания (при фиксированном w), т.е. конкретный вид, принимаемый случайным процессом X(t), его траектория.
Таким образом, случайный процесс X (t, w) совмещает в себе черты случайной величины и функции. Если зафиксировать значение аргумента t, случайный процесс превращается в обычную случайную величину, если зафиксировать w, то в результате каждого испытания он превращается в обычную неслучайную функцию.
Как и случайная величина, случайный процесс может быть описан числовыми характеристиками.
Математическим ожиданием случайного процесса X(t) называется неслучайная функция ax(t), которая при любом значении переменной t равна математическому ожиданию соответствующего сечения случайного процесса X(t), т.е. ax(t) = M [X(t)].
Дисперсией случайного процесса X(t) называется неслучайная функция. Dx(t), при любом значении переменной t равная дисперсии соответствующего сечения случайного процесса X(t), т.е. Dx(t) = D [X(t)].
Средним квадратическим отклонением  случайного процесса X(t) называется арифметическое значение корня квадратного из его дисперсии, т.е.
случайного процесса X(t) называется арифметическое значение корня квадратного из его дисперсии, т.е. 
Математическое ожидание случайного процесса характеризует среднюю траекторию всех возможных его реализаций, а его дисперсия или среднее квадратическое отклонение – р а з б р о с реализаций относительно средней траектории.
Корреляционной функцией случайного процесса X(t) называется неслучайная функция
двух переменных t1 и t2, которая при каждой паре переменных t1и t2 равна ковариации соответствующих сечений X(t1) и X(t2) случайного процесса.
Нормированной корреляционной функцией случайного процесса X(t) называется функция
Основные понятия теории массового обслуживания
На практике часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Примерами таких систем являются телефонные системы, ремонтные мастерские, вычислительные комплексы, билетные кассы, магазины, парикмахерские и т.п.
Каждая СМО состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые будем называть каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы и др. По числу каналов СМО подразделяют на одноканальные и многоканальные.
Заявки поступают в СМО обычно не регулярно, а случайно, образуя так называемый случайный поток заявок (требований). Обслуживание заявок, вообще говоря, также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (они либо становятся в очередь, либо покидают СМО необслуженными), в другие же периоды СМО работает с недогрузкой или простаивает.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоками заявок.
В качестве показателей эффективности СМО используются: среднее число заявок, обслуживаемых в единицу времени; среднее число заявок в очереди; среднее время ожидания обслуживания; вероятность отказа в обслуживании без ожидания; вероятность того, что число заявок в очереди превысит определенное значение, и т.п.
СМО делят на два основных типа (класса): СМО с отказами и СМО с ожиданием (очередью). В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, заявка на телефонный разговор в момент, когда все каналы заняты, получает отказ и покидает СМО необслуженной). В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.
СМО с ожиданием подразделяются на разные виды в зависимости от того, как организована очередь: с ограниченной или неограниченной длиной очереди, с ограниченным временем ожидания и т.п.
Понятие марковского случайного процесса
Процесс работы СМО представляет собой случайный процесс.
Процесс называется процессом с дискретными состояниям, если его возможные состояния S1, S2, S3… можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны.
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких-то событий (например, прихода новой заявки, окончания обслуживания и т.п.).
Математический анализ работы СМО существенно упрощается, если процесс этой работы – марковский. Случайный процесс называется марковским или случайным процессом без последействия, если для любого момента времени to вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент to и не зависят от того, когда и как система пришла в это состояние.
Пример марковского процесса: система S – счетчик в такси. Состояние системы в момент t характеризуется числом километров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент to счетчик показывает So. Вероятность того, что в момент t to счетчик покажет то или иное число километров (точнее, соответствующее число рублей) S1, зависит от So, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента to.
Потоки событий
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (например, поток вызовов на телефонной станции, поток отказов ЭВМ, поток покупателей и т.п.).
Поток характеризуется интенсивностью X – частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока есть величина постоянная: Например, поток автомобилей на городском проспекте не является стационарным в течение суток, но этот поток можно считать стационарным в определенное время суток, скажем, в часы пик. В этом случае фактическое число проходящих автомобилей в единицу времени (например, в каждую минуту) может заметно различаться, но среднее их число постоянно и не будет зависеть от времени.
Поток событий называется потоком без последействия, если для – любых-двух непересекающихся участков времени Т1 и Т2 число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Например, поток пассажиров, входящих в метро, практически не имеет последействия. А, скажем, поток покупателей, отходящих с покупками от прилавка, уже имеет последействие (хотя бы потому, что интервал времени между отдельными покупателями не может быть меньше, чем минимальное время обслуживания каждого из них).
Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени At двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами. Например, поток поездов, подходящих к станции, ординарен, а поток вагонов не ординарен.
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. Название «простейший» объясняется тем, что СМО с простейшими потоками имеет наиболее простое математическое описание. Регулярный поток не является простейшим, так как обладает последействием: моменты появления событий в таком потоке жестко зафиксированы.
ЗАКЛЮЧЕНИЕ
Современные приложения дисперсионного анализа охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.
Благодаря автоматизации дисперсионного анализа исследователь может проводить различные статистические исследования с применение ЭВМ, затрачивая при этом меньше времени и усилий на расчеты данных. В настоящее время существует множество пакетов прикладных программ, в которых реализован аппарат дисперсионного анализа. Наиболее распространенными являются такие программные продукты как:
- MS Excel;
- Statistica;
- Stadia;
- SPSS.
В современных статистических программных продуктах реализованы большинство статистических методов. С развитием алгоритмических языков программирования стало возможным создавать дополнительные блоки по обработке статистических данных.
Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.
Дисперсионный анализ является мощным современным статистическим методом обработки и анализа экспериментальных данных в психологии, биологии, медицине и других науках. Он очень тесно связан с конкретной методологией планирования и проведения экспериментальных исследований.
Дисперсионный анализ применяется во всех областях научных исследований, где необходимо проанализировать влияние различных факторов на исследуемую переменную.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Кремер Н.Ш. Теория вероятности и математическая статистика. М.: Юнити – Дана, 2002.-343с.
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003.-523с.
www.sutd.ru
www.conf.mitme.ru
www.pedklin.ru
www.webcenter.ru
www.infections.ru
www.encycl.yandex.ru
www.infosport.ru
www.medtrust.ru
www.flax.net.ru






 ,
, .
.












