Рекомендации для составления рабочей программы.
VII вид обучения.
8 КЛАСС
Курс рассчитан на 3 часа в неделю, всего 102 часа.
Программа составлена с учетом особенностей детей. От учащихся нельзя требовать запоминания и вывода сложных формул, доказательства теорем, решения нестандартных, трудоёмких заданий.
В связи с этим ряд тем изучается ознакомительно:
Понятие об иррациональном числе.
Арифметические действия над действительными числами.
Понятие о корне n-й степени из числа.
Функция у = 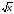 , ее график.
, ее график.
Решение квадратичных уравнений выделением квадратного двучлена.
Теорема Виета.
Формула корней квадратного уравнения, у которого второй коэффициент является четным числом.
Доказательство числовых и алгебраических неравенств.
Содержание программы
1. Рациональные дроби (23 ч.)
Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Возведение дроби в степень. Преобразование рациональных выражений. Функция у = 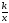 и ее график.
и ее график.
Основная цель – выработать умение выполнять преобразования рациональных дробей.
Главное место занимают алгоритмы действий с дробями. Задания не должны быть громоздкими. Знаменатели дробей должны раскладываться на множители способом вынесения общего множителя за скобки или по формуле а2 – в2 = (а – в)(а + в).
В комбинированных заданиях на все действия с дробями знаменатели должны быть разложенными на множители. Не рассматриваем случаи, когда требуется свернуть знаменатель по формуле квадрат суммы (разности) двух выражений.
Свойства функции у = 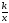 рассматривать на конкретных графиках.
рассматривать на конкретных графиках.
В ходе изучения данной темы учащиеся должны усвоить алгоритм выполнения действий с рациональными дробями; выполнять комбинированные задания в простых ситуациях, строить график функции
у = 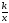 .
.
2. Квадратные корни (19 ч.)
Понятие об иррациональном числе. Общие сведения о действительных числах. Понятие арифметического квадратного корня. Уравнение х2 = а, свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Функция у = 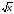 , ее график.
, ее график.
Основная цель – выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся знакомятся с понятием иррационального числа, действительного числа.
Основное внимание обращаем на выработку умений извлекать квадратный корень, выполнять преобразования выражений, содержащих квадратные корни; достаточно ограничиться вынесением числового множителя из-под знака корня и внесением числового множителя под знак корня, а также освобождением от иррациональности в знаменателе в выражениях вида 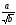 .
.
В ходе изучения данной темы учащиеся должны научиться извлекать квадратный корень, использовать свойства арифметического квадратного корня, вносить, множитель под знак корня, выносить множитель из-под знака корня.
3. Квадратные уравнения (21 ч.)
Определение квадратного уравнения. Решение квадратных уравнений по формуле. Решение несложных задач с помощью квадратных уравнений. Решение дробно-рациональных уравнений.
Основная цель – выработать умения решать квадратные уравнения, дробные рациональные уравнения, применять их к решению задач.
Основное внимание уделяем решению уравнений вида ах2 + bх +с = 0, где а ≠ 0 по формуле корней. Рассматриваем одну (основную) формулу без вывода. Изучаем решение квадратных уравнений выделением квадрата двучлена, теорему Виета.
При рассмотрении дробных рациональных уравнений обращаем внимание на необходимость дополнительных исследований, позволяющих исключить посторонние корни. При этом не рассматриваем такие уравнения, знаменатели которых требуют применения формул квадрата суммы (разности) двух выражений.
При решении тестовых задач решаем задачи, связанные с периметром и площадью прямоугольника.
В ходе изучения данной темы учащиеся должны усвоить алгоритм решения квадратного уравнения, уметь решать квадратные уравнения.
4. Неравенства (20 ч.)
Числовые неравенства и их свойства. По членное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке выражений х + у, ху. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.
Основная цель – выработать у учащихся умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств рассматриваем на конкретных примерах и не доказываем. Даем понятие о числовых промежутках, вводим соответствующие обозначения. При решении неравенств используем свойства равносильности неравенств, которые разъясняем на конкретных примерах. Особое внимание уделяем отработке умения решать неравенства вида ах в, ах остановившись специально на случае, когда а
Умение решать линейные неравенства является основой для решения систем двух линейных неравенств с одной переменной.
В ходе изучения данной темы учащиеся должны решать линейные неравенства с одной переменной и их системы.
5. Степень с целым показателем. Элементы статистики. (11 ч.)
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Основная цель – сформировать понятие степени с целым отрицательным показателем; выработать умение выполнять преобразования простейших выражений, содержащих степень с целым показателем, ввести понятие стандартного вида числа, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации
В теме рассматриваем свойства степеней с целыми показателями (без доказательства). Специальное внимание следует уделить записи чисел в стандартном виде, которая используется в физике, технике.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот.
В ходе изучения темы учащиеся должны усвоить определение степени с отрицательным показателем; уметь выполнять преобразования простейших выражений, содержащих степени с целыми показателями, находить по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах.
6. Повторение (8 ч.)
Требования к уровню подготовки учащихся
В результате изучения курса алгебры 8 класса учащиеся должны
знать/понимать:
основные термины, связанные с уравнениями, функциями, степенями, правильно употреблять их, понимать в речи учителя, в постановке задачи;
как используются математические формулы, уравнения и неравенства;
уметь:
выполнять основные действия со степенями с целыми показателями, с алгебраическими дробями; выполнять преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать квадратные уравнения;
решать линейные неравенства с одной переменной и их системы;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для :
решения несложных практических расчетных задач;
выполнения расчетов по формулам, понимая формулу как алгоритм вычисления;
- выстраивания аргументации при доказательстве и в диалоге.
Программа составляется по учебнику для 8 класса /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова; под ред. С.А. Теляковского – М.: Просвещение.





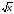 , ее график.
, ее график.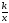 и ее график.
и ее график.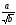 .
.
















