Решение прикладных задач в математике как способ развития мирровозрения у обучающихся

Решение прикладных задач в математике

как способ развития мирровозрения у обучающихся

Выполнил преподаватель ДВГКГБ

Дутова О.А.

«Что значит владение математикой? Это есть умение решать задачи. Причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности». Д. Пойа

ЦЕЛИ

• развивать гибкость мышления, творческое отношение к изучаемому предмету, формировать независимость математического мышления в ходе решения задач.
• на примере решения прикладных задач с простейшими жизненными ситуациями показать применение методов математического моделирования, поддержать этим интерес к предмету.

ПЛАН

• Математика и игра.
• Зачем вообще нужно решать

математические задачи?

• Виды задач.
• Примеры задач
• Результаты опроса среди студентов ДВГКГБ
• Заключение

Математика и игра

• Современные требования к уроку предполагают использование новых подходов в преподавании математики. При подготовке к уроку преподаватель все чаще использует компьютерные технологии. Уроки с использованием презентаций становятся более насыщенными, эффективными и дают возможность развивать у студентов интерес к предмету, познавательную активность, творческий подход.
• На уроке применение интерактивной доски должно наряду с самой темой привлечь внимание студентов к прикладной направленности математики. Одновременно текстовые задачи рассматриваются не только как прикладные, но и как умственные манипуляторы. Существует важное сходство между математикой и детской игрой: в обоих случаях исключительно важно творческое воображение. Потребность в умственных манипуляциях никогда не кончается, она присуща и профессиональным математикам на самом высоком уровне.
• Решение любой задачи, особенно сложной, требует от ребят напряженного труда и упорства. А упорство проявляется, если задача интересна. Значит, нужно преподавателю подбирать такие задачи, которые студенты хотели бы решать. Чаще всего интерес вызывают задачи практического содержания.

Зачем вообще нужно решать математические задачи? Кто ни слышал вечного изречения, что математика – царица всех наук? Но математика  - сложная наука, а решение задач требует множества знаний. А никто не задумывался, зачем вообще нужно решать математические задачи? Во-первых, математика – это и правда основа многих наук. Без математики изучение химии, физики, и даже некоторых разделов биологии не возможно. Без математики и решения задач не могут обойтись такие профессии, как: экономист, программист, инженер, врач, архитектор, военный. Кроме того задачи по математике еще и развивают логическое мышление. Такое умение пригодится и в обычной жизни. Умение решать задачи – один из основных показателей уровня математического развития. Решение задач – работа несколько необычная, а именно умственная работа. Существует несколько видов задач. По характеру объектов задачи различаются на прикладные задачи и математические задачи .

Виды задач Прикладная (практическая) задача – это задача, поставленная вне математики и решаемая математическими средствами . Математическая задача – это задача, которая выполняется посредством умозаключения, вычисления. По отношении к теории задачи делятся на стандартные задачи и нестандартные задачи. Стандартные задачи - это задачи, для решения которых в школьном курсе математики имеются готовые правила (в виде словесного алгоритма, формулы, тождества и т.д.) или эти правила непосредственно следуют из правил, теорем, определений программного минимума Нестандартные задачи – это задачи, способ решения которых не находится в распоряжении субъекта. По характеру требований задачи делятся на три вида: нахождение (распознавание) искомых, задачи на преобразование или построение и задачи на доказательство и  объяснение.

Прикладные задачи могут быть использованы с разной  целью, они могут заинтересовать или мотивировать, развивать умственную деятельность, объяснять соотношение между математикой и другими дисциплинами. Прикладная задача повышает интерес учащихся к самому предмету, поскольку для подавляющего большинства ценность математического образования состоит в ее практических возможностях. Под задачей с практическим содержанием понимается математическая задача, фабула которой раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит ее с использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций. Я считаю, что нужно работать над реализацией прикладной направленности обучения серьезно, ведь она влечет за собой развитие познавательной активности у учащихся. В педагогических исследованиях прикладная направленность математики понимается как содержательная и методическая связь школьного курса с практикой, что предполагает у учащихся умений, необходимых для решения средствами математики практических задач. А так как в основе их решения лежит математическое моделирование, то для реализации прикладной направленности необходимо организовать обучение школьников элементам моделирования, которыми с дидактической точки зрения являются учебные действия, выполняемые в процессе решения задач.   Развитие у учащихся правильных представлений о характере отражения математикой явлений и процессов реального мира, роли математического моделирования в научном познании и в практике имеют большое значение для формирования диалектико - материалистического мировоззрения учащихся.

ПРИМЕРЫ ЗАДАЧ Задача 1. За один рейс автомашина МАЗ-25 перевозит 25 тонн груза. Сколько тонн груза она перевезет за k рейсов? Найдите значение выражения при k равном 10, 5, 0. . Задача 2. За 3 часа работы 1 экскаватор вынул 555 м3  земли. Сколько кубических метров земли вынет второй экскаватор за 4 часа, если в час он вынимает на 15 м3 больше, чем первый? Задача 3. Московская фирма «Выбор» в первом квартале 1999 года продала на сумму 962 тысяч 530 рублей, во втором квартале на 18 тысяч 234 рублей больше, чем в первом. На какую сумму было продано товаров во втором квартале? Задача 4 В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ. Задача5 На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей зависимых событий определить вероятность того, что обе детали окажутся стандартными.

• Задача Молодой предприниматель Михайлов Юрий в свете экономического кризиса решил выкупить нерентабельное провинциальное перерабатывающее предприятие и пригласил экономиста Гульдерова Германа помочь с расчетами по оптимизации расходов. Одна из задач поставленных перед Германом была следующая: найти, при каких условиях расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет наименьшим.

• Вспомним 3 этапа математического моделирования, применяемые при решении задач на оптимизацию
• 1 этап. Составление математической модели.
• 2 этап. Работа с составленной моделью.
• 3 этап. Ответ на вопрос задачи.
• Наименьший расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой.
• Полезно обратить внимание ребят на то, что в нашей стране выпускаются ежегодно сотни миллионов банок консервов в жестяной упаковке. Экономия 1% жести на изготовление каждой банки позволит за счет сэкономленного материала дополнительно изготовить несколько миллионов новых банок. Вместе с тем промышленность нередко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением минимизации отходов при изготовлении банок, соображениями торговой эстетики.

НЕКОТОРЫЕ РАЗДЕЛЫ МАТЕМАТИКИ, КОТОРЫЕ ПОЗВОЛЯЮТ РЕШАТЬ ЗАДАЧИ ПРИКЛАДНОГО ХАРАКТЕРА

• Применение элементов математического анализа п позволяет более эффективно решать многие задачи повышенной сложности. Применение производной для решения задач требует от учащихся нетрадиционного мышления. Следует отметить, что знание нестандартных методов и приемов решения задач способствует развитию нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельность (вычислительная техника, экономика, физика, химия и т.д.)

• Элементы комбинаторики и теории вероятностей позволяют решать задачи прикладного характера., позволяют определять случайное событие и его вероятность. Стереометрия позволяет развивать пространственное воображение и решать задачи, которые позволяют затем переносить полученные знания для использования в работе архитектора и строителя. Бухгалтеру необходимо решать задачи прикладного характера при изучении всего курса математики, так как с математикой у него связана вся его практическая деятельность.

Результаты опроса среди студентов ДВГКГБ

• Какие вам нравится решать задачи по математике?
• 1) стандартные
• 2) нестандартные
• 3) мне все равно

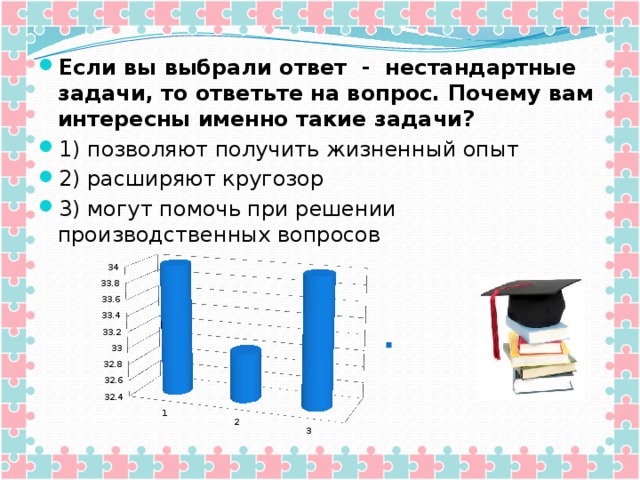
• Если вы выбрали ответ - нестандартные задачи, то ответьте на вопрос. Почему вам интересны именно такие задачи?
• 1) позволяют получить жизненный опыт
• 2) расширяют кругозор
• 3) могут помочь при решении производственных вопросов

Заключение

• Роль математики в самых разнообразных сторонах жизни общества резко возросла и, несомненно, будет возрастать и далее. Между учебным предметом и математикой, применяемой на практике, есть определённая пропасть. Мостом между ними может и должно послужить существенное усиление прикладной направленности курса математики .
•  

Спасибо за внимание !