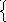| Этап урока | Деятельность учителя | Деятельность учащихся | Личностные УУД Познавательные УУД Регулятивные УУД Коммуникативные УУД
|
| Мотивация учащихся | Здравствуйте, ребята. Сегодня наш урок я хотела начать с философской загадки Вальтера. Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами? Итак, у нас всего 45 минут и мне очень хотелось, чтобы это время пролетело для вас незаметно и с пользой. На каждом этапе урока вы будете самостоятельно оценивать свою работу с помощью листов самооценки. |
Время | Личностные Самоопределение |
| Устная работа
Актуализация знаний | слайд 1 Всё о системах вспомни ты,
Своими знаньями блесни! Фронтальный опрос. Что называется системой двух линейных уравнений с двумя переменными?
Что называется решением системы двух линейных уравнений с двумя переменными? .
Что значит решить систему уравнений с двумя переменными?
Является ли пара чисел (1;1) решением системы уравнений 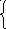 3х – 4у = -1, 3х – 4у = -1, х + 4у = 5.
Какие методы решения системы уравнений с двумя переменными вы знаете? Что используете при решении системы уравнений? В чем заключается способ подстановки и графический способ? (Сформулировать правила).
С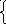 лайд 3. Решить систему уравнений лайд 3. Решить систему уравнений 2х + у = 4, х – у = 8. 1 вариант методом подстановки 2 вариант графическим способом. |
Системой двух линейных уравнений с двумя неизвестными называются 2 линейных уравнения с двумя переменными, объединенные фигурной скобкой. Фигурная скобка означает, что оба уравнения должны выполняться одновременно
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Да, пара чисел является решением каждого уравнения
Метод подстановки. Графический способ. Алгоритмом Графический способ 1.Выразить у через х в каждом уравнении; 2.построить в одной системе координат график каждого уравнения; 3.определить координаты точки пересечения; 4.Записать ответ: х=…; у=… , или (х; у). Способ подстановки 1.Из какого-либо уравнения выразить одну переменную через другую; 2.подставить полученное выражение для переменной в другое уравнение и решить его; 3.сделать подстановку найденного значения переменной и вычислить значение второй переменной; 4.записать ответ: х=…; у=… .
Два ученика работают у доски
Ефимова Н. Меднова Е. | Личностные УУД оценивание знаний по пройденному материалу Познавательные выдвижение гипотез и их обоснование
построение логической цепи рассуждений
выбор способа действий Коммуникативные Постановка вопросов, разрешение затруднений
Регулятивные Планирование |
| Постановка цели и задачи урока. Мотивация учебной деятельности учащихся. | Слайд 4. (создание проблемной ситуации) 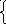 13х+17у=43, 13х+17у=43, 14х-17у=11. Фронтальный опрос: Выберем уравнение, в котором удобно одну переменную выразить через другую.
Т.е. в данной ситуации нам не подходит изученные ранее методы. Какой выход из данной ситуации? Обратите внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной. Посмотрите на систему уравнений и подумайте, как из двух данных уравнений получить одно уравнение с одной переменной. Сложить уравнения. Что значит сложить уравнения? По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Сформулируйте тему и цель урока
Запись темы урока Решение системы линейных уравнений методом сложения 13х+17у+14х-7у=43+11 27х+0=54 27х=54 ; х=54:27; х= 2
Слайд 5 Средь алгоритмов правильный найди,
И выбор свой подробно поясни! Слайд 6. ( приложение №2) алгоритм решения |
Такого уравнения нет
Найти новый метод.
Решение системы линейных уравнений методом сложения. Составит алгоритм решения системы линейных уравнений методом сложения. Научиться применять алгоритм при решении систем линейных уравнений
Составление алгоритма | Личностные умение осознанно применять полученные знания на практике умение осознанно строить алгоритм Познавательные формулирование познавательной целипостроение логической цепи рассужденийвыдвижение гипотез и их обоснование Коммуникативные Постановка вопросов, разрешение затруднений Регулятивные Целеполагание |
|
| Физкультминутка Слайд 7. |
|
|
| Первичное усвоение новых знаний | Работа с учебником стр. 207. Метод решения системы линейных уравнений основывается на утверждении. Слайд 8-11 Устная работа Решить системы линейных уравнений способом сложения а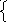 + b=2, + b=2, a – b=6.
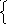
3z – t=4, 3z + t=8.
|
Читают в учебнике
При ответе используют алгоритм решения системы линейных уравнений 2а + 0 = 8 2а = 8; а = 8:2; а=4 4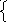 +b =2, b = 2 – 4 = -2 +b =2, b = 2 – 4 = -2 а = 4 b = -2
6z+0=12 6z=12; z=12:6=2; z= 2 3*2+t=8; 6+t=8; t=8-6=2 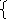 z=2 z=2 t=2 | Личностные Самоопределение
Познавательные поиск и выделение информации
построение логической цепи рассуждений Коммуникативные Инициативное сотрудничество в поиске и сборе информации
Умение аргументировать свою точку зрения Регулятивные составление плана и последовательности действий |
| Первичное закрепление | Слайд 12 Работа у доски №1047 (5) Обсудить, какой из способов рациональнее. |
Девяткина Д. | Личностные умение осознанно применять алгоритм при решении Познавательные поиск и выделение информации
построение логической цепи рассуждений Регулятивные предвосхищение результатов деятельности |
| Первичная проверка понимания | Слайд 13
Всё что по теме обязаны вы знать, Пора в самостоятельной работе показать! 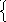 2х – 5у = 9, 2х – 5у = 9, - 2х +4у = - 7. 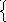
2х – 3у = 2, 2х – у = 0.
|
Работа в группах
Взаимопроверка
| Личностные умение осознанно применять алгоритм сложения при решении систем Познавательные анализ успехов и затруднений Коммуникативные работа в парах Регулятивные сопоставить свой результат с заданным эталоном |
| Оценивание ответов | А теперь поработай учителем ты
И работу свою оцени!
| Выставляют оценки. Сообщают результаты |
|
| Домашнее задание | слайд 17 П. 28, выучить алгоритм решения системы линейных уравнений 2. на «3» №1048 (1) методом подстановки и методом сложения. на «4» №1048 (1) решить графическим способом, методом подстановки и методом сложения. на «5» №1048 (1) решить графическим способом, методом подстановки и методом сложения №1048(3) | записывают в дневник | |
| Рефлексия (подведение итогов занятия) | Слайд 18 Предлагает ответить на вопросы.
Итак, закончен наш урок. Надеюсь, он пошёл вам впрок! Спасибо за работу и вниманье. Желаю всем успехов! До свиданья! |
| Личностные самооценка Познавательные анализ успехов и затруднений Коммуникативные аргументированно отвечать на вопрос |






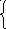 3х – 4у = -1,
3х – 4у = -1,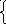 лайд 3. Решить систему уравнений
лайд 3. Решить систему уравнений + b=2,
+ b=2, 
 z=2
z=2 2х – 5у = 9,
2х – 5у = 9,