Решение транспортной задачи в Excel

И. В. Синёв,

преподаватель вычислительной техники

Кировского транспортного техникума.

Логический подход к решению транспортной задачи с помощью Excel.

С появлением компьютеров решение многих задач стало сводиться к элементарному вводу данных, а алгоритм решения знают только составители программ. Это хорошо для практических целей, но для процесса обучения такие программы не подходят, т.к. теряется возможность развития у студента логического мышления. Компьютер должен помогать студенту при выполнении элементарных, но громоздких вычислений, а логическая часть решения задачи должна оставаться за студентом. Понятно, что составление таких программ ляжет на плечи преподавателей, поскольку стандартные программы для народного хозяйства, написанные профессиональными программистами, должны облегчать труд человека, а преподаватель должен подготовить студентов к созданию таких программ или алгоритмов. Для этого студент сам должен принимать участие в решении задач, чтобы научиться создавать их самостоятельно. Рассмотрим одну из таких программ.

Студентам практически всех технических ВУЗов приходиться решать так называемую транспортную задачу. Транспортная задача представляет собой задачу линей­ного программирования, её можно решать симплекс-методом. Однако специфическая структура условий задачи позво­лила разработать более эффективные вычислительные ме­тоды.

Внимание к транспортным задачам обусловлено тем, что задачи подобного типа, во-первых, часто встречаются в практических работах по исследованию операций и, во-вто­рых, к ним сводятся многие другие задачи линейного программирования: сетевая задача, задача о назначениях, за­дача календарного планирования и т.п.

Для решения транспортной задачи разработан целый ряд методов. Здесь рассмотрен метод, который нашёл широкое применение в практике, а именно метод потенциалов (модификация распределитель­ного метода). Данная задача легко решается с помощью компьютера, например на языках Pascal, FoxPro. Однако при полностью автоматизированном решении студенты, как сказано выше, лишены возможности логически мыслить, т.к. сразу, после ввода данных, получают оптимальный план, а при «ручном» решении много времени затрачивается на рутинную работу – математические вычисления. Этих недостатков лишена программа в Excel, созданная автором. В ней присутствует и самостоятельное мышление при построении опорных планов, и компьютерная помощь при громоздких вычислениях. Эта программа будет полезной студентам, которые изучают методы решения оптимизационных задач, а также преподавателям вычислительной техники и программистам.

Теория и математическая постановка транспортной задачи хорошо изложена во многих учебниках. Однако следует напомнить основные положения задачи.

Даны размеры m запасов (a_i) и n потребностей (b_j), и матрица стоимости перевозки единицы груза от каждого поставщика к каждому потребителю (C_ij).

Нужно составить план перевозок, чтобы общая стоимость всех перевозок (F), была минимальной.

З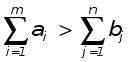адача представляет собой транспортную задачу линейного программирования. Она может быть открытого типа, когда

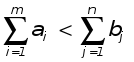
, или , или

При превышении общего объема запасов над спросом (или наоборот), в таблицу данных добавляется фиктивный пункт потребления (или запасов). Потребления (или запасы) в этом пункте принимаются равным превышению общего объема наличия продукта над суммарным объемом спроса (или наоборот), то есть (в первом случае)

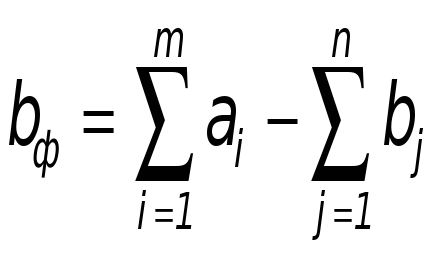
Стоимость (C_ij) в клетках этого столбца таблице равняется нулю. По аналогии действуем и во втором случае.

После этих преобразований задача становится транспортной задачей линейного программирования закрытого типа, потому что

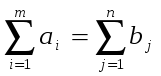
Рассмотрим решение задачи методом потенциалов.

Строим первый опорный план. При этом используем метод двойного преимущества: сначала выбираем клетки с минимальной стоимостью по каждой строке, потом - по каждому столбцу.

Для построения первого опорного плана используют и другие методы, например, северо-западного угла.

Этот опорный план с данными представляем в первой таблице. Справа от таблицы добавляем столбец потенциала U_i, снизу - строка потенциала V_j . В первой строке принимаем U_i=0 и дальше заполняем значение потенциалов по строкам и столбцам таблицы, где есть значения (базисные клетки) таким образом, чтобы выполнялось уравнение: С_ij=U_i+V_j.

В плане должно быть (m+n-1) базисных клеток.

Если оценка какой-то свободной клетки S_ij=C_ij-(U_i+V_j)

Тогда переделываем план, избрав эту клетку (если их несколько - выбираем максимальную по модулю), вписав в неё минимальное из существующих значений базисных клеток. Другие значения базисных клеток преобразуем таким образом, чтобы сумма спроса и потребности по строкам и столбцам оставалась неизменной.

То есть, увеличиваем или уменьшаем на это значение другие базисные клетки. Цикл пересчёта – это многоугольник с прямыми углами в базисных (заполненных) клетках, в которых и делаем этот пересчет.

На каждом этапе преобразования транспортной таблицы можно подсчитывать общие расходы для сравнения с предыдущим планом.

Когда для всех клеток выполнится условие Sij =0 - план будет оптимальным, то есть общие расходы F - минимальны.

Следует отметить, - если в полученном оптимальном опорном плане есть хотя бы одна оценка свободной клетки, которая равна нулю, то такой оптимальный план неоднозначен, то есть при той же минимальной стоимости может быть и другой оптимальный опорный план, что не меняет цели решенной задачи.

Д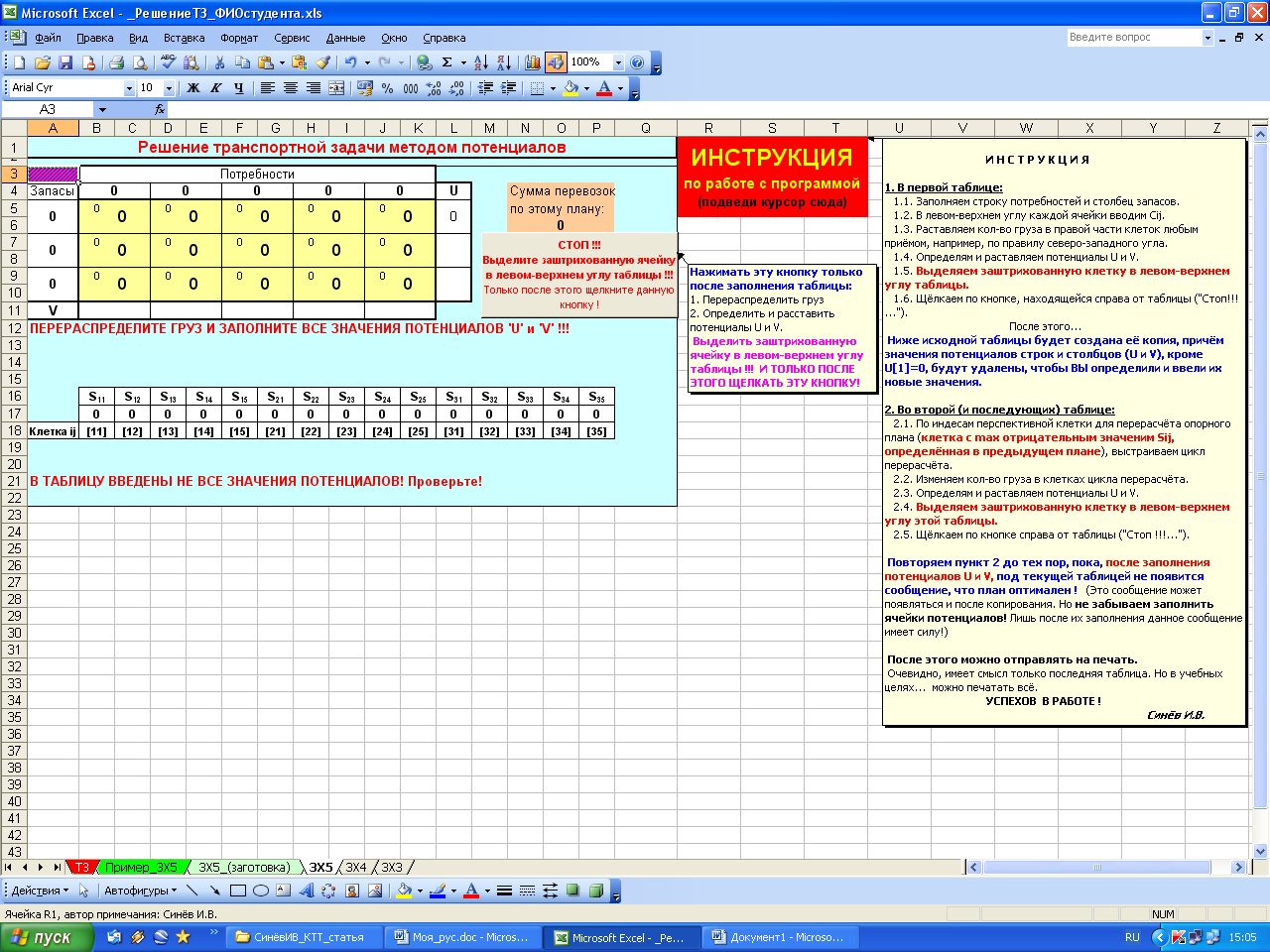алее приведена исходная таблица (в начале работы в файле-книге Excel) для решения транспортной задачи (3х5), т.е. 3 поставщика и 5 потребителей (рис.1). Заготовки таблиц для любого сочетания поставщиков и потребителей можно выполнить на отдельных листах Excel.

Рис.1 Исходная таблица в Excel для решения транспортной задачи (3х5)

Программа снабжена инструкцией и подсказками. На листе, с помощью «Примечания», создается инструкция по работе с программой, которая появляется при наведении курсора на соответствующую ячейку (в данной программе – R1).

Содержание инструкции приведено ниже.

ИНСТРУКЦИЯ ПО РАБОТЕ С ПРОГРАММОЙ

1. В первой (исходной) таблице:

1.1. Заполняем строку потребностей и столбец запасов.

1.2. В левом верхнем углу каждой ячейки вводим C_ij (тариф перевозки единицы груза).

1.3. Расставляем кол-во груза в правой части клеток любым приёмом, например, по правилу северо-западного угла.

1.4. Определяем и расставляем потенциалы U и V.

1.5. Выделяем заштрихованную клетку в левом верхнем углу таблицы.

1.6. Щёлкаем по кнопке, находящейся справа от таблицы ("Стоп!!! ...").

После этого ниже исходной таблицы будет создана её копия, причём значения потенциалов строк и столбцов (U и V), кроме U[1]=0, будут удалены, чтобы вы определили и ввели их новые значения.

2. Во второй (и последующих) таблице(ах):

2.1. По индексам перспективной клетки для перерасчёта опорного плана (клетка с max отрицательным значением Sij = Сij — (Ui + Vj), - оценка свободной клетки, определённая в предыдущем плане), выстраиваем цикл перерасчёта.

2.2. Изменяем количество груза в клетках цикла перерасчёта.

2.3. Определяем и растравляем потенциалы U и V.

2.4. Выделяем заштрихованную клетку в левом верхнем углу этой таблицы.

2.5. Щёлкаем по кнопке справа от таблицы ("Стоп !!!...").

После выполнения этих действий с помощью макроса будет выполнено копирование последнего и вставка очередного опорного плана, в котором нужно перераспределить груз, но без значений потенциалов.

Заполняем значения потенциалов U и V. Если не все ячейки со значениями потенциалов заполнены – программа выдаст соответствующее сообщение.

Повторяем пункт 2 до тех пор, пока, после заполнения потенциалов U и V, под текущей таблицей не появится сообщение, что план оптимален! После этого можно отправлять на печать.

Очевидно, имеет смысл только последняя таблица. Но мы говорили об учебных целях, а это означает, что можно и нужно печатать всё.

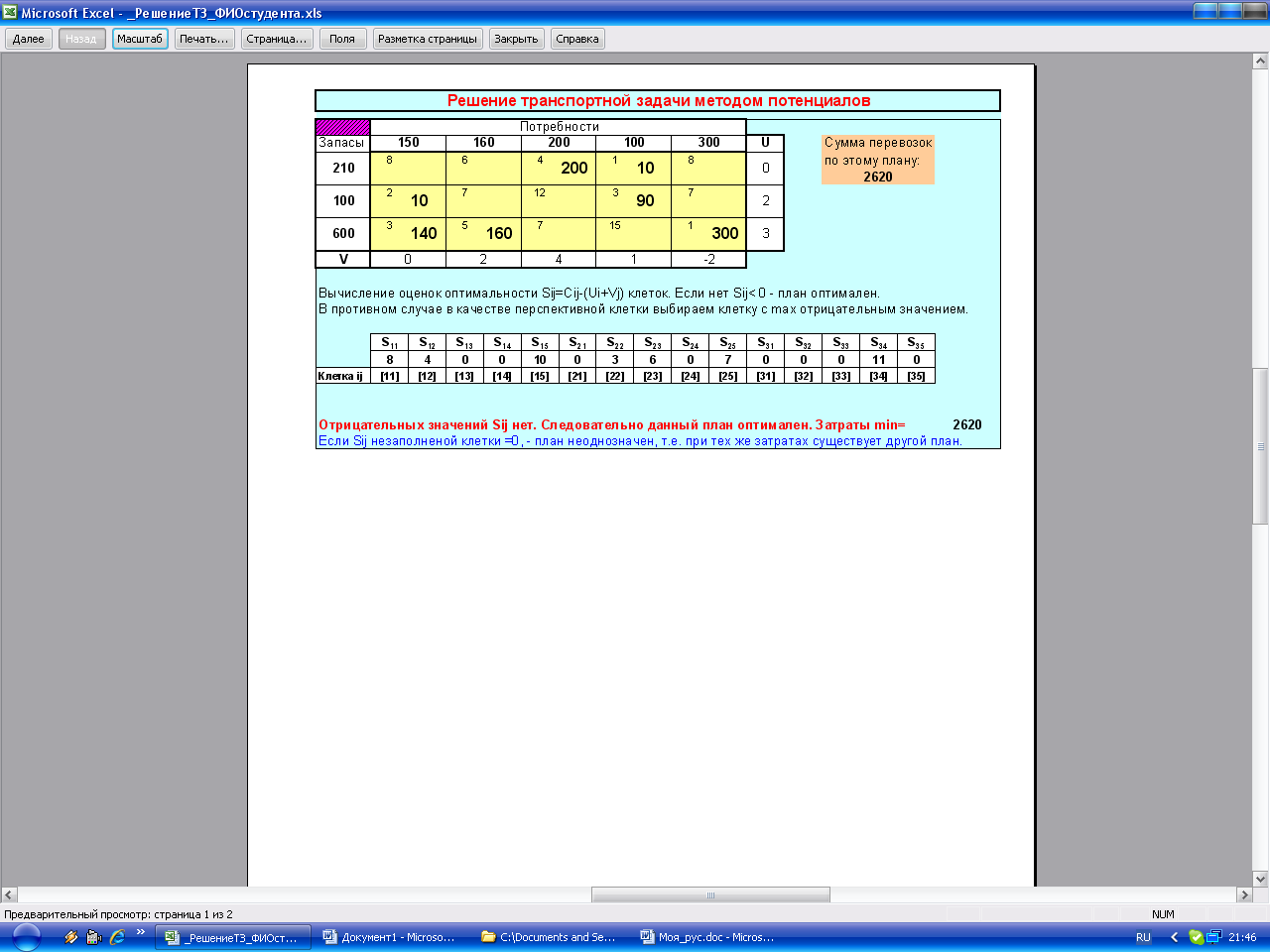
Пример распечатки решения приведен в приложении на рис. 2-а, 2-б. Формулы в файле-книге Excel, по которым происходят вычисления, представить на рисунках электронной таблицы из-за их громоздкости невозможно. Кроме того, соответствие ссылкам лучше просмотреть в самой программе, т.к., например, формула

=ЕСЛИ(ИЛИ(B11="";D11="";F11="";H11="";J11="";L7="";L9="";H20=0);"";

ГПР(H20;B17:P18;2;ЛОЖЬ))

будет непонятной без наличия самой таблицы.

В данной работе не приводится порядок создания макросов, поскольку это не является принципиальным. Скопировать и вставить таблицу опорного плана, а также удалить значение потенциалов можно и без макроса. Но в данном случае, макрос позволяет не тратить время на рутинную работу и таким образом он лишь совершенствует программу. Его запуск осуществляется кликом по кнопке «СТОП!!! Выделите заштрихованную ячейку в левом верхнем углу таблицы!!! Только после этого щелкните данную кнопку». Это нужно для того, чтобы макрос при копировании опорного плана определил, относительно какой ячейки производить копирование и вставку.

Цикл пересчёта – многоугольник с прямыми углами вычерчивается в Excel с помощью панели инструментов «Рисование».

Замечания, предложения и заказы на приобретение данной бесплатной программы просьбы направлять по адресу: sinjov_igor@mail.ru

Синёву Игорю Вячеславовичу.

ЛИТЕРАТУРА

1. Деордица Ю.С., Нефедов Ю.М. – Исследование операций в планировании и управлении: Учебн. пособие. – К.: Выща шк., 1991. – 270с..

2. Глушаков С.В., Сурядный А.С. Microsoft Offise 2000: Учебный курс. – Харьков: Фолио; Ростов-на-Дону; Феникс, 2001.–500 с.

Приложение

Рис.2-а Распечатка решения транспортной задачи (начало)

Рис.2-б Распечатка решения транспортной задачи (окончание)

Примечание. Поскольку в приведенном примере в оптимальном плане S₃₂=0 (незаполненная клетка), то такой оптимальный план неоднозначен, то есть при той же минимальной стоимости может быть и другой оптимальный план, что не меняет цели решенной задачи. Альтернативный оптимальный план для данного примера представлен ниже.

9