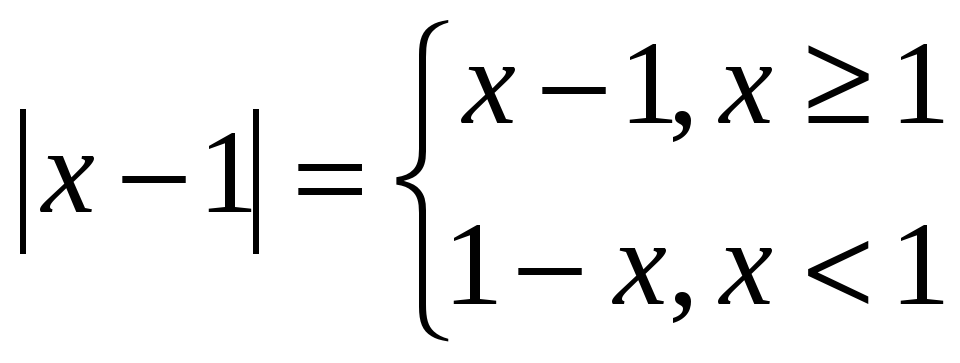Решение уравнений по модулю

Краевая научно-практическая конференция «Эврика»

Малая академия наук учащихся Кубани.

Секция: «Математика».

Тема:

Алгебраические решение

уравнений,

содержащих модули.

Сведения об авторе:

Воробьева Анастасия Юрьевна ученица 8 «А» класса МОУСОШ6

имени Н.Г. Чернышева станицьи Казанскои Кавказского района Краснодарского края Дата рождения:23.02.92г. Паспорт :0306 251527 Домашний адрес:

ул,Кропотккна,238

Сведения о руководителе:

Бондаренко Енгения Леонидовна, учитель математики первой квалификационной категории

МОУСОШ6 имени Н.Г. Чернышева станицы Казанской Кавказского района Краснодарского края.

Аннотация.

Тема исследования: «Алгебраическое решение уравнений, содержащих модули».

Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6- го — 8-го класса, где они проходят самые азы уравнений с модулями, я выбрала именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.

Задача : сознательно овладеть системой знаний и умений об алгебраических уравнениях, содержащих модуль, учится с 8 класса выполнять задания С из ЕГЭ, готовится к поступлению в ВУЗ.

Автор исследует актуальную тему математики, решая задачу сознательного овладения системой знаний и умений об алгебраических уравнениях, содержащих неизвестное под знаком модуля, готовится к выполнению заданий С из ЕГЭ, поступлению в ВУЗ.

В работе подробно освещена теоретическая часть уравнения с модулем, доказаны теоремы, рассмотрен аналитический способ решения уравнений, содержащих модули.

Особый интерес у автора вызвало решение нестандартных уравнений, содержащих модуль. Приведены примеры решения уравнений с модулем из диагностической краевой контрольной работы декабрь 2006г. 10 кл.

Использована обширная литература.

Данная работа лишь начало в исследовании важной и интересной темы, но делает честь молодому автору, ученице 8 класса Воробьевой Анастасии.

Эти исследования обеспечат ей развитие математических способностей, подготовку автору поступления в ВУЗ, ориентацию на профессию, существенным образом связанной с математикой.

Содержание:

Введение…………………………………………………………………… 4

1 .Понятия и определения ………………………………………………...4

2.доказательство теорем …………………………………………………..5

3.Способы решение уравнений, содержащих модуль ………………….6

3.1.Решение нестандартных уравнения, содержащие модуль.. ………...8

Заключение ………………………………………………………………...9

Литература ………………………………………………………………..11

Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6-го — 8-го класса, где они проходят самые азы уравнений с модулями, я выбрала именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.

Задача : сознательно овладеть системой знаний и умений об алгебраических уравнениях, содержащих модуль, учится с 8 класса выполнять задания С из ЕГЭ, готовится к поступлению в ВУЗ.

Введение.

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.

В архитектуре - это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.

В технике - это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и

т.п.

Модуль объемного сжатия (в физике) - отношение нормального напряжения в материале к относительному удлинению.

1. Понятия и определения:

Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы:

Уравнение-это равенство, содержащее переменные.

Уравнение с модулем - это уравнение, содержащие переменную под знаком абсолютной величины (под знаком модуля). Например: 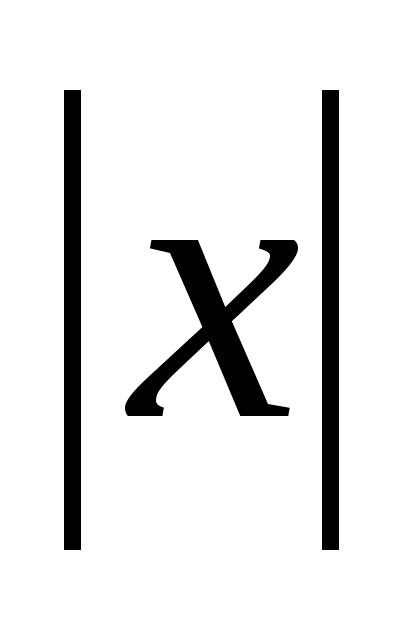= 1

Решить уравнение-это значит найти все его корни, или доказать, что корней нет, В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно:

Модуль - абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой.

1. Доказательство теорем

Определение. Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна -а, если а меньше нуля:

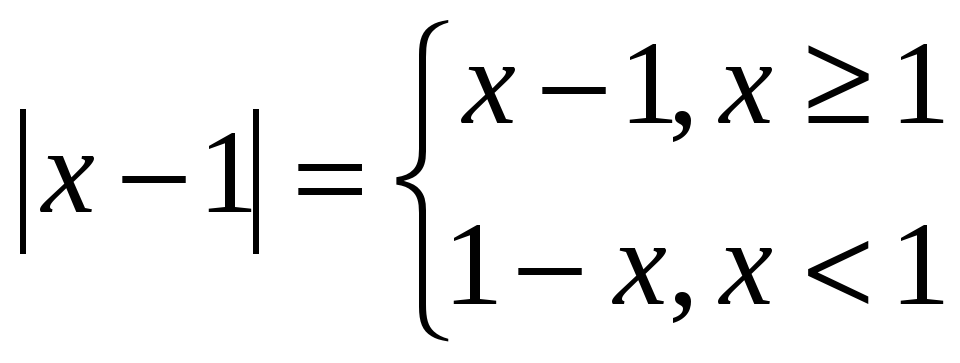
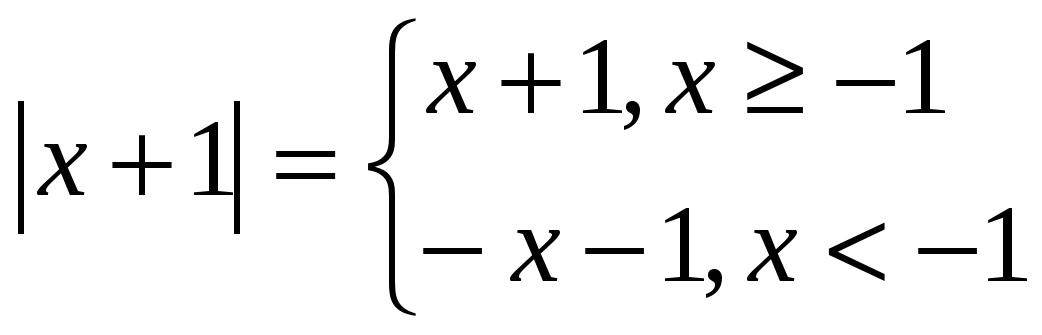
Из определения следует, что для любого действительного числа а,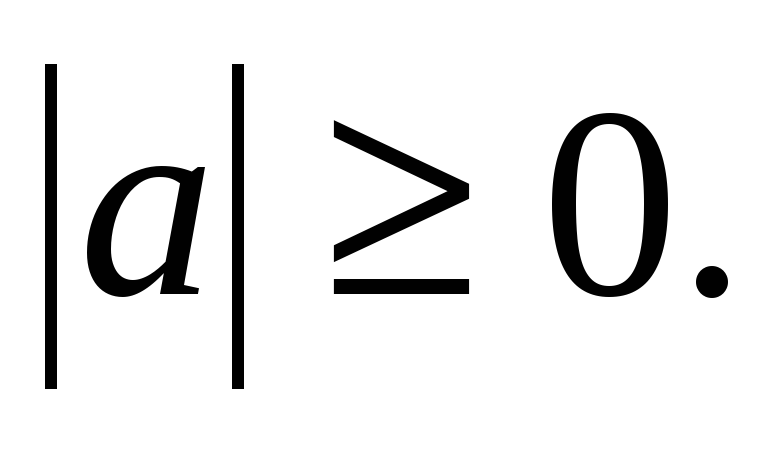

Теорема 1. Абсолютная величина действительного числа а0 равна большему из двух чисел а или -а.

Доказательство:

1. Если число а положительно, то -а отрицательно, т. е. -а

Например, число 5 положительно, тогда -5 - отрицательно и -5

В этом случае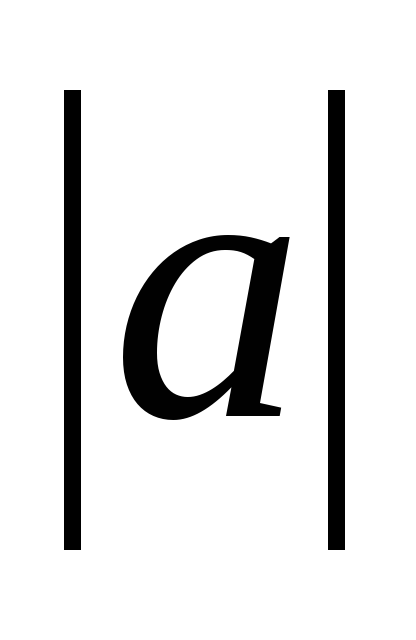 = - а, т. е. совпадает с большим из двух чисел а и - а.

2. Если а отрицательно, тогда -а положительно и а - а, т. е. большим числом является - а. По определению, в этом случае, = -а - снова, равно большему из двух чисел -а и а.

Следствие 1. Из теоремы следует, что = .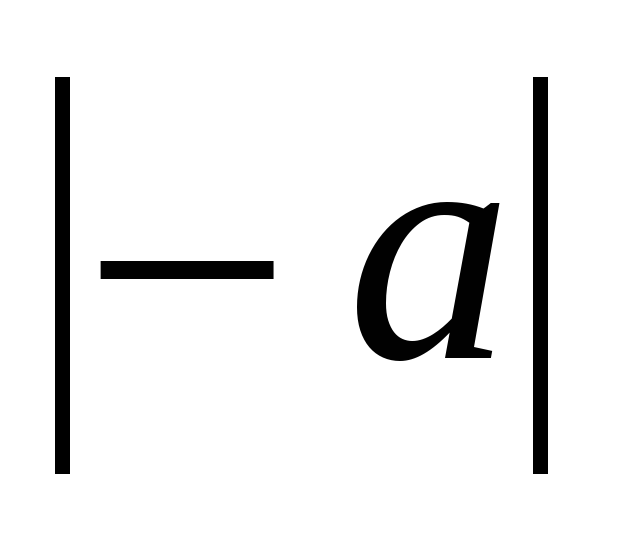

В самом деле, как 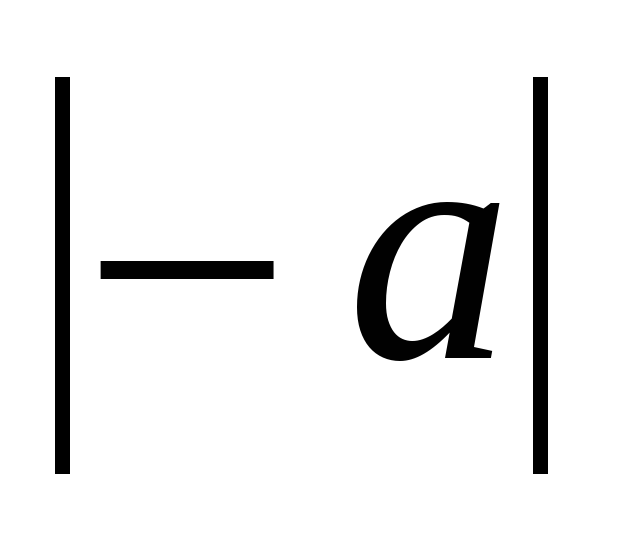, так и равны большему из чисел -а и а, а значит, равны между собой.

Следствие 2. для любого действительного числа а справедливы неравенства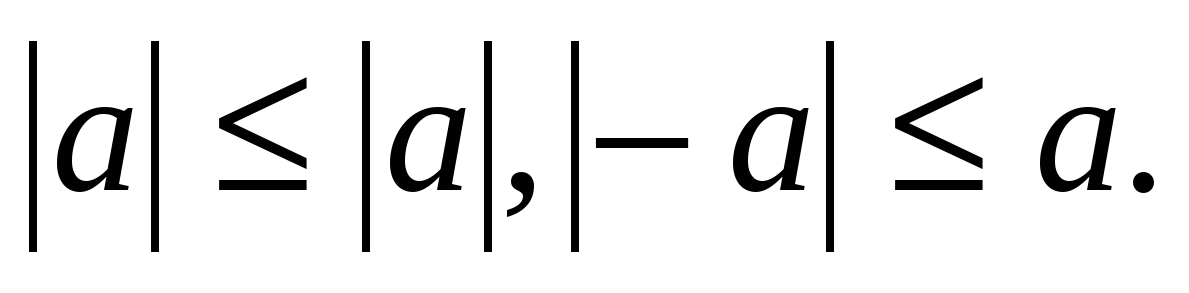

З.Способы решения уравнений содержащих модуль.

Для решения уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа. Мы решим несколько примеров одним и тем же способом и посмотрим, какой из способов окажется проще для решения уравнений, содержащих модуль.

Два числа, модули которых равны, либо равны между собой, либо отличаются лишь знаком:

если = 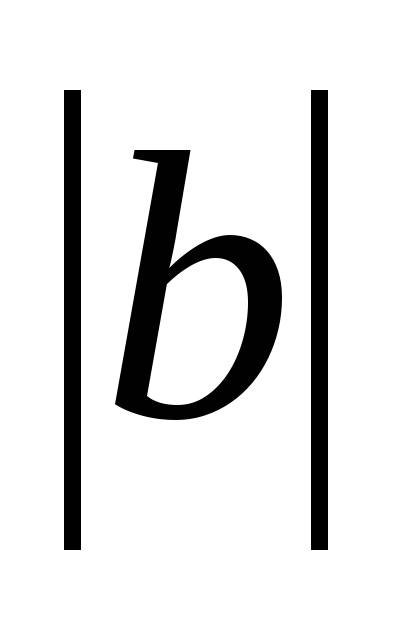, то либо а = b, либо а = -b. Либо –а = b.

Применим это замечание к решению уравнения .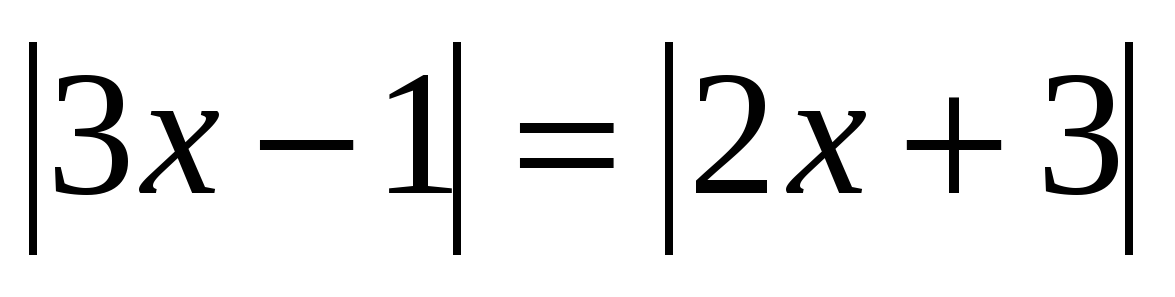

В силу сказанного выше из этого уравнения вытекает, что либо 3х-1 = 2х+3,

либо 3х-1= - (2х+3). Корнем первого уравнения является число 4, а второго — число - 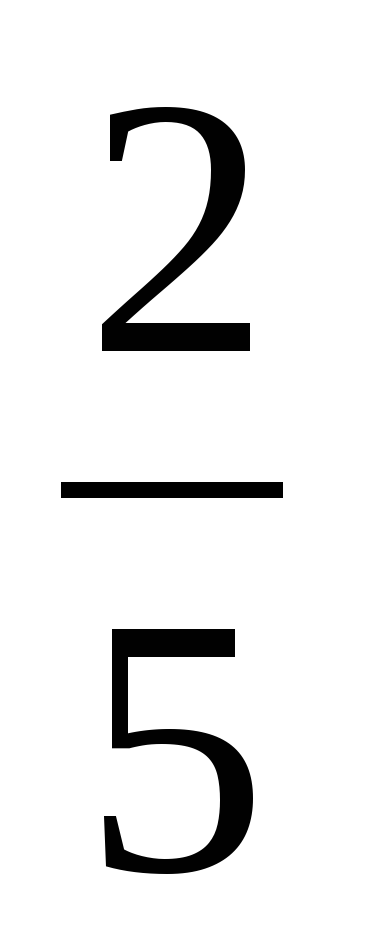. Итак, решение исходного уравнения имеет вид Х₁ =4, Х₂ = -.

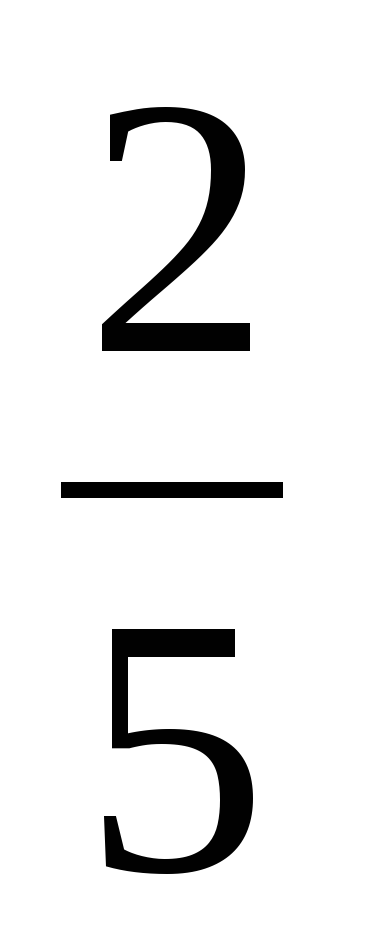В других случаях бывает полезно сначала установить, в каких точках обращаются в нуль выражения, стоящие под знаком модуля. Эти точки разбивают числовую ось на промежутки, внутри которых выражения сохраняют постоянный знак (промежутки знакопостоянства) Это позволяет освободиться на каждом из таких промежутков от знака модуля и свести задачу к решению нескольких уравнений — по одному па каждом промежутке.

Пример 2. Решим аналитически уравнение 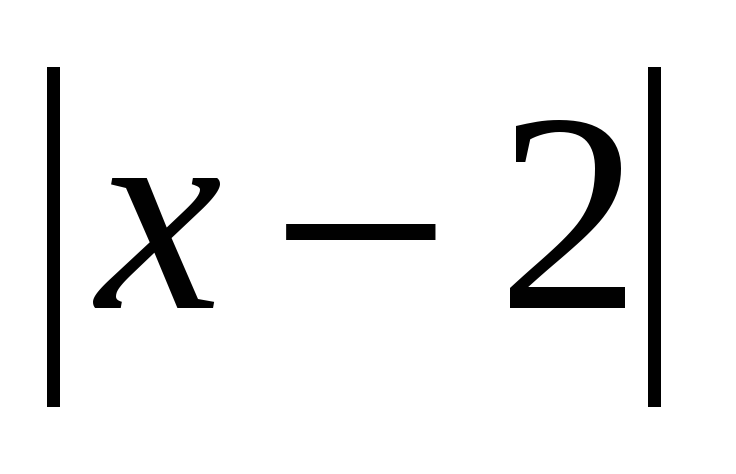=3

Аналитическое решение

1-й способ

Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т. е. х - 2 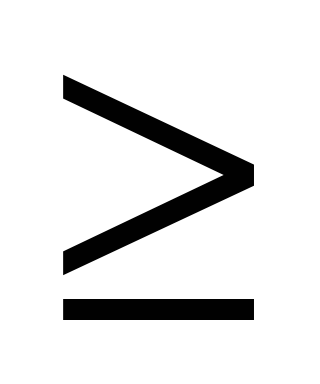0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: х - 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: - (х - 2) = 3. или х - 2=-3

Таким образом, получаем, либо х - 2 = 3, либо х - 2 = -3. Решая полученные уравнения, находим: х₁ = 5, х₂ = - 1.

Ответ: х₁ = 5, х₂ = -1.

Умножая второе равенство - а на -1 (при этом знак неравенства изменится на

противоположный), мы получим следующие неравенства: а , а 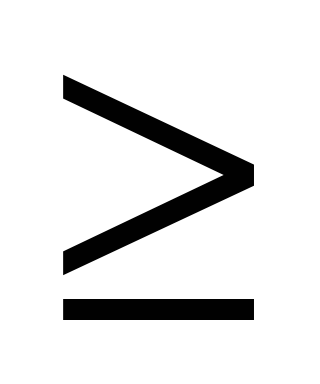- , справедливые для любого действительного числа а. Объединяя последние два неравенства в одно, получаем:

—а

Теорема 2. Абсолютная величина любого действительного числа а равна арифметическому квадратному корню из а²: =.

В самом деле, если а 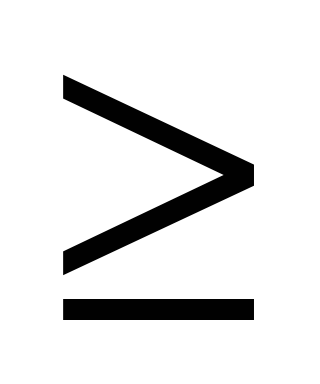0, то, по определению модуля числа, будем иметь = а.

С другой стороны, при а 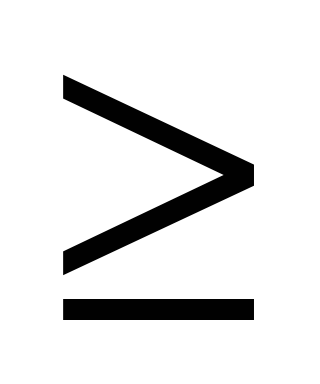0, = а, а значит = .

Если а = -а и = - а, и в этом случае =

Эта теорема дает возможность при решении некоторых задач заменять на

Геометрически означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.

Если а 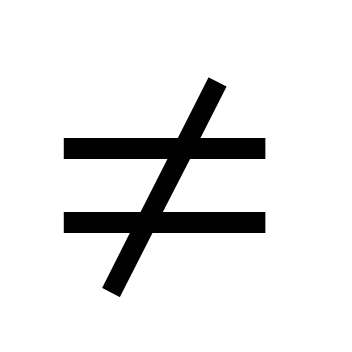0, то на координатной прямой существует две точки а и -а, равноудаленной от нуля, модули которых равны.

Если а 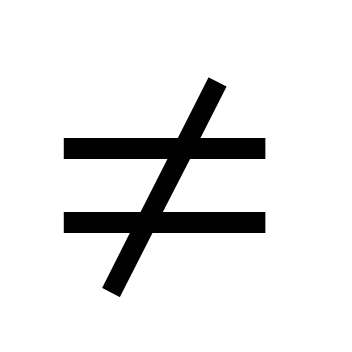0, то на координатной прямой изображается точкой 0 (см. рис 1.)

Рис. 1

Пример 1

Заметим, что 5 — модуль чисел 5 и —5. Решив великое

множество примеров, можно заметить тождество

=

Пример 2. Решим аналитически уравнение 1 + = 0,5.

Аналитическое решение

Преобразуем уравнение: 1 + = 0,5

=0,5-1

= -0,5

Понятно, что в этом случае уравнение не имеет решений, так как, по определению, модуль всегда неотрицателен.

Ответ: решений нет.

3.1Решение нестандартных уравнений, содержащие модуль

В других случаях бывает полезно сначала установить, в каких точках обращаются в нуль выражения, стоящие под знаком модуля. Эти точки разбивают числовую ось на промежутки, внутри которых выражения сохраняют постоянный знак (промежутки знакопостоякства). Это позволяет освободиться на каждом из таких промежутков от знака модуля и свести задачу к решению нескольких уравнений — по одному на каждом промежутке.

Пример 1.

Выражение х² - 5х равно нулю соответственно в точках 0;5

х²-5х =0

х = 0;х = 5

Эти точки разбивают числовую ось на промежутки. [2,8;5) и ( 5; ).

Заключение

Я поставила перед собой цель глубже изучить решение уравнений, содержащие знак модуля. В результате работы над темой я научилась не просто решать эти уравнения, но и решать уравнения аналитическим способом, также самой составлять такие задачи.

В моей работе предложены приемы решения некоторых заданий. Я выбрала эту тему, потому что с развитием новых технологий модуль имет все большую практическую значимость, используются как способы контроля за качеством и применяются во многих видах деятельности. К тому же мне интересно заниматься изучением модуля числа.

Я считаю, что достигла поставленной цели, и в дальнейшем надеюсь продолжить более углубленное изучение материала.

Используемая литература.

1«Спецкурс по математике. 10 класс». Бутузов В. Ф., Колягин Ю. М. и др.

1. «Алгебра. 9 класс». Никольский С. М., Потапов М. К., Решетников Н.Н., Шевкин А.В.

2. «Алгебра. 8 класс». Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.

3. «Математика. Материалы для углубленного изучения в 8-9 классах». Галицкий М.

4. «Алгебра и начала анализа. 10 класс». Мордкович А. Г., Семенов П. В.

5. «История математики в школе 9-11 классы». Глейзер Г. И.