Россия, Ханты-Мансийск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 16.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 26.04.2025 20:58
Джура Елена Николаевна
учитель математики, методист
64 года
11 959
3 220 
Местоположение
Специализация
Решение уравнений с дробями 5 класс
Категория:
Математика
31.01.2017 10:31
Просмотр содержимого документа
«Решение уравнений с дробями 5 класс»
Обыкновенные дроби
часть 3
5 класс
- Сложение дробей с одинаковыми знаменателями.
- Вычитание дробей с одинаковыми знаменателями.
- Решение уравнений.
- Решение задач.
Сложение дробей с одинаковыми знаменателями.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить прежним.
3
3+1
1
4
=
+
=
8
8
8
8
1
8
3
3+5
5
=
=
+
=
8
8
8
8
Вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
3
3-1
1
2
=
-
=
8
8
8
8
0
3
3
-
=
8
8
Решение уравнений.
При решении уравнений необходимо пользоваться правилами решения уравнений, свойствами сложения и вычитания.
Решение уравнений с применением свойств.
Решение уравнений с использованием правил.
Решите уравнение.
Подсказка 1
Выражение в левой части уравнения является суммой.
51
32
=
;
х
+
85
85
32
51
Подсказка 2
слагаемое + слагаемое = сумма.
х
=
-
;
85
85
19
х
=
.
85
Подсказка 3
Чтобы найди неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
19
Ответ:
85
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
12
78
=
;
у
-
90
90
12
78
Подсказка 2
уменьшаемое – вычитаемое = разность
у
=
-
;
90
90
66
у
=
.
90
Чтобы найди неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Подсказка 3
66
Ответ:
90
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
8
11
а
=
-
;
25
25
8
11
Подсказка 2
уменьшаемое – вычитаемое = разность
а
=
+
;
25
25
19
а
=
.
Чтобы найди неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Подсказка 3
25
19
Ответ:
25
Решите уравнение.
(
7
3
18
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
+
х
+
=
(
;
19
19
19
В левой части уравнения выражение является суммой.
Подсказка 1
3
18
7
+
=
х
;
-
19
19
19
3
11
=
х
+
Подсказка 2
;
Неизвестное содержится в слагаемом.
19
19
11
3
х
=
;
-
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
-
у
=
(
+
;
44
44
44
В левой части уравнения выражение является разностью.
Подсказка 1
5
37
17
=
у
+
;
-
44
44
44
5
20
=
у
+
Подсказка 2
;
Неизвестное содержится в вычитаемом.
44
44
20
5
у
=
;
-
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
18
8
21
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
b
+
=
-
;
73
73
73
Подсказка 1
В левой части уравнения выражение является разностью.
18
8
21
b
+
;
=
+
73
73
73
29
18
=
+
Подсказка 2
Неизвестное содержится в уменьшаемом.
b
;
73
73
29
18
=
b
;
-
73
73
11
11
b
Ответ:
.
=
73
73
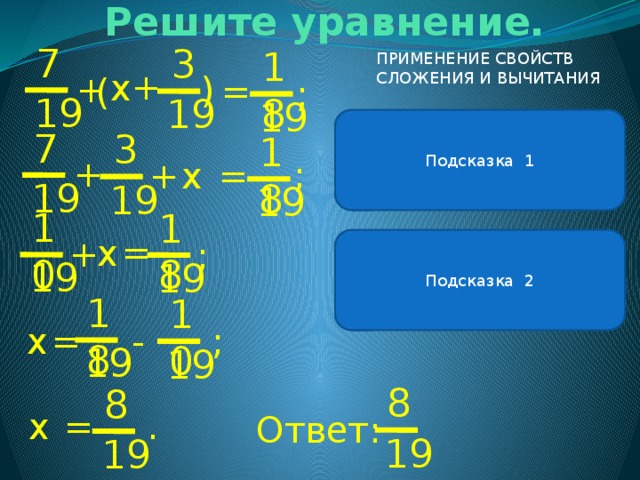
Решите уравнение.
(
7
3
18
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
х
+
=
(
;
19
19
19
В левой части уравнения можно применить сочетательное свойство сложения .
Подсказка 1
7
3
18
+
;
+
=
х
19
19
19
10
18
=
х
+
Подсказка 2
;
Чтобы к числу прибавить сумму , можно к этому числу прибавить сначала одно слагаемое, а потом другое.
19
19
18
10
х
=
;
-
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
-
у
=
(
+
;
44
44
44
В левой части уравнения можно применить свойство вычитания суммы из числа. .
Подсказка 1
37
5
17
-
;
-
=
у
44
44
44
32
17
=
у
-
Подсказка 2
;
Чтобы из числа вычесть сумму, можно вычесть сначала одно слагаемое, а потом другое.
44
44
32
17
у
=
;
-
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
8
18
21
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
b
=
-
;
73
73
73
Подсказка 1
В левой части уравнения можно применить свойство вычитания числа из суммы.
18
21
8
-
;
+
=
b
73
73
73
10
21
=
b
+
Подсказка 2
Чтобы вычесть число из суммы, можно сначала вычесть это число из одного слагаемого, а потом прибавить другое.
;
73
73
21
10
=
b
;
-
73
73
11
11
b
.
=
Ответ:
73
73
Решение задач.
2
В первый день Саша прочитал книги, а во второй день - книги. Сколько страниц прочитал Саша за два дня, если в книге 144 страницы?
9
4
9
144 стр.
4
2
9
9
2
4
6
1) + = (книги) – прочитал Саша за 2 дня.
9
9
9
2) 144 : 9 ∙ 6 = 96 (стр.)
Ответ: За 2 дня Саша прочитал 96 страниц.
Решение задач.
5
В первый день Маша прочитала книги, а во второй день - книги. Сколько страниц в книге, если Маша за два дня прочитала 36 страниц?
12
4
12
36 стр.
4
5
12
12
5
4
9
1) + = (книги) – прочитала Маша за 2 дня.
12
12
12
2) 36 : 9 ∙ 12 = 48 (стр.)
Ответ: В книге 48 страниц.
© 2017, Джура Елена Николаевна 40795 345
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
