Решение задач на построение в paintbrush

РЕШЕНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ В PAINTBRUSH

Одним из популярных направлений использования компьютеров является компьютерная графика. Существует много разных графических редакторов для вы­полнения графических задач на ПК. Наиболее распространенным и доступным для работы в школе является растровый графический редактор Microsoft Paint (в раз­личных версиях Windows — PaintBrush, PBrush), являющийся стандартным прило­жением операционной системы Windows. В литературе можно найти много публикаций, посвященных изучению как инструментов Paint так и его воз­можностей по созданию различных рисунков и использованию его на уроках в школе.

Рассмотрим несколько другой аспект применения бога­тейших возможностей Paint — использование графического редактора для реше­ния задач на построение. Умение решать такие задачи необходимо, во-первых, для создания различных рисунков в Paint, для решения возникающих при этом проб­лем. Во-вторых, это позволит научиться не только решать геометрические задачи на построение, но и лучше изучить геометрию. Всем известна формулировка геометри­ческих задач на построение «Построить при помощи циркуля и линейки». Мы пред­лагаем новый тип геометрических задач на построение: «Построить средствами Paint». Эти задачи можно использовать как материал для проведения интегриро­ванных уроков математики и информатики.

Задачи, которые предлагается решить средствами Paint.

Для начала рассмотрим простейшие базовые задачи (упражнения).

Упражнение 1. Провести горизонтальную и вертикальную линии.

Здесь при построении надо обратить внимание на то, чтобы линия не имела изло­мов (рис. 1, 2). Заметим, что излом происходит в середине отрезка. На рис. 1 и 2 изображены варианты правильного и неправильного выполнения упражнения.

Рис.1

Рис.2

Рис.3

Рис.4

Упражнение 2. Провести перпендикуляр к вертикальной или горизонтальной прямой.

Это упражнение выполнить несложно, решение сводится к выполнению преды­дущего упражнения.

Упражнение 3. Провести прямую под углом 45° к горизонтали.

Прямая будет составлять 45° с горизонталью, если при увеличении прямой инст­рументом Лупа она вся будет состоять из одинаковых элементарных фрагментов (пикселей), имеющих форму квадрата, и все квадраты будут касаться друг друга не сторонами (рис. 3), а вершинами (рис. 4).

Отметим, что выполнение заданий упражнений 1—3, т. е. проведение вертикаль­ной, горизонтальной линий и линии под углом в 45° к горизонтали, можно элемен­тарно проводить, используя инструмент Прямая при нажатой клавише Shift.

Упражнение 4. а) Провести параллельные прямые. б) Провести равные отрезки.

Для этого можно воспользоваться следующим приемом: выделить отрезок исход­ной прямой и скопировать его. Это можно сделать разными способами:

1. нажать комбинацию клавиш Ctrl+C, затем Ctrl+V;

2. воспользоваться последовательно командами Правка-Копировать-Вставить;

3. щелкнуть правой кнопкой мыши на выделенном рисунке, затем выбрать команду Копировать, опять щелкнуть правой кнопкой в произвольном месте и выбрать команду Вставить;

4) перенести (скопиро­вать) выделенный рисунок при нажатой левой кнопке мыши и одновременно нажа­той клавише Ctrl в нужное место (рис. 5, 6).

Упражнение 5. Провести перпендикуляр к произвольному отрезку прямой.

Для этого можно воспользоваться следующим приемом: выделить отрезок исход­ной прямой и скопировать его. Теперь для построения искомого пер­пендикуляра необходимо щелкнуть правой кнопкой мыши и в контекстном меню выбрать команду Отразить/повернуть, Повернуть на угол 90° (рис. 7). Получен­ный отрезок переместить так, чтобы он проходил через точку, в которой требуется провести перпендикуляр (точка А на рис. 8).

Рис.5

Рис.6

Рис.7

Рис.8

Упражнение 6. Разделить отрезок пополам.

Нарисовать отрезок АВ (рис. 9), затем, выбрав инструмент Прямоугольник, по­местить указатель мыши в начало отрезка и построить прямоугольник ADBC, в ко­тором данный отрезок является диагональю (рис. 10). Теперь, используя инструмент Линия, провести вторую диагональ CD полученного прямоугольника, которая и пройдет через середину О данного отрезка (рис. 11).

Ч

А

А

D тобы разделить пополам горизонтальный отрезок АВ, можно также построить прямоугольник со стороной АВ, провести его диагонали и из точки пересечения диа­гоналей опустить перпендикуляр на АВ, который попадет в середину отрезка (точка О на рис. 12). Аналогично можно разделить пополам и вертикальный отре­зок. Отметим, что эту задачу можно решить, используя тот факт, что излом при про­ведении отрезка происходит в его середине.

В

С

Рис.9

В

Рис. 10

Рис.11

Рис.12

Упражнение 7. Найти центр окружности.

Графический редактор Paint при рисова­нии окружности не указывает ее центр. Вследствие этого иногда возникает необхо­димость определения центра построенной окружности. Кроме того, специфической особенностью рисования окружности в Paint является то, что исходной точкой указателя мыши при использовании инструмента Окружность является не центр окружности, а вершина описанного около нее квадрата. Следовательно, для построе­ния окружности необходимо определить не ее центр и радиус, а любую вершину такого квадрата.

Эту задачу, впрочем, как и все другие, можно решить разными способами.

Для нахождения центра окружности можно использовать инструмент Прямо­угольник, подвести курсор к любой точке окружности и построить прямоугольник, вписанный в данную окружность (рис. 13). Затем инструментом Линия провести его диагонали, точка пересечения которых и будет являться центром искомой окружно­сти (точка О на рис. 14).

Другой способ нахождения центра окружности (рис. 15): увеличим окружность инструментом Лупа, определим середины горизонтальной (точка А) и вертикальной (точка С) дуг окружности, представленных при увеличении отрезками прямых. Затем проведем два взаимно перпендикулярных диаметра АВ и CD через середины этих отрезков, точка пересечения которых (О), очевидно, и будет являться центром искомой окружности.

Рис. 13 Рис. 14

Теперь уже нетрудно решить следующую задачу.

Рис. 15

Упражнение 8. Разделить угол пополам.

П А усть дан угол ABC (рис. 16). Построим окружность произвольного радиуса в произвольном месте экрана (см. упражнение 6) и найдем центр О построенной окружности (рис. 17). Затем выделим и будем перемещать ее так, чтобы она оказа­лась вписанной в данный угол (рис. 18). Проведем прямую ВО (инструмент Прямая), проходящую через вершину угла и центр вписанной окружности (рис. 19). Эта прямая будет являться биссектрисой угла ABC, т. е. будет делить его пополам.

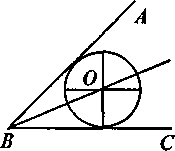
В

С

Рис 16. Рис. 17 Рис. 18 Рис. 19

Упражнение 9. Вписать окружность в квадрат.

Эта задача решается элементарно, если вспомнить, что при использовании инст­румента Окружность исходное положение указателя мыши является вершиной квадрата, описанного около окружности. Следовательно, чтобы нарисовать окруж­ность, вписанную в данный квадрат, необходимо воспользоваться инструментом Окружность, установить указатель мыши в вершину данного квадрата и нарисовать окружность, касающуюся сторон данного квадрата.

Гораздо труднее решить следующую задачу.

Упражнение 10. Вписать квадрат в окружность.

Эту задачу можно решить следующим способом. Прежде всего, надо найти центр окружности (см. упражнение 6). Затем из центра окружности инструментом Линия провести радиус под углом 45° к горизонтали (см. упражнение 3) — получим верши­ну искомого квадрата. Теперь, воспользовавшись инструментом Прямоугольник, при нажатой и удерживаемой клавише Shift нарисовать искомый квадрат, вписан­ный в окружность.

Упражнение 11. Вписать правильный треугольник в окружность (построить правильный треугольник).

Найдем центр окружности (см. упражнение 6) (рис. 20), выделим радиус ON и скопируем его (см. упражнение 4) так, чтобы его копия оказалась горизонтальной хордой АА' окружности (рис. 21). Так как длина хорды АА' равна длине радиу­са ON, то она стягивает на окружности дугу в 60°. Теперь из любого конца хорды (например, из точки А) восстановим к ней перпендикуляр АВ до пересечения с окружностью в точке В (рис. 22). Легко доказать, что полученная хорда отсекает от окружности дугу ANB, содержащую 120°. Соединив концы полученной хорды с противоположным концом диаметра (точкой С), получим искомый правильный треугольник ABC (рис. 23).

Рис 20. Рис. 21 Рис. 22 Рис. 23

Упражнение 12. Построить фигуры, симметричные данной относительно вер­тикальной или горизонтальной прямой.

Это упражнение выполнить несложно.

Упражнение 13. Построить фигуры, симметричные данной относительно любой заданной точки (поворотная симметрия).

Для начала, естественно, надо построить исходную фигуру и указать точку А — центр симметрии (рис. 39). Затем необходимо выделить данную фигуру вместе с точкой, скопировать ее и повернуть на 180° (рис. 40). Теперь следует переместить копию полученного рисунка так, чтобы совпали точки симметрии обоих рисунков (рис. 41). В результате получится центрально симметричная относительно указан­ной точки фигура.

Рис. 39

Рис. 40

Рис. 41

Задание 3. Построить рисунки, зеркально симметричные рисунку, полученному в результате выполнения упражнения 18, относительно вертикальной и горизон­тальной осей (рис. 42).

Рис. 42