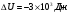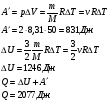Решение задач по теме «Первый закон термодинамики».
Цели урока: помочь учащимся осмыслить физическое содержание первого закона термодинамики;
рассматривая качественные задачи, показать, что проявления действия первого закона термодинамики имеют место в окружающем мире;
на примере решения конкретных расчетных задач научить учащихся применять первое начало термодинамики к описанию изопроцессов в идеальном газе.
Тип урока: закрепление материала.
Вид урока: решение задач..
Ход урока.
1. Оргмомент
2. Актуализация знаний
1.Какая из приведённых ниже формул является математическим выражением первого закона термодинамики?
а/ 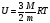 б/
б/ 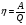 в/
в/ 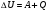

2.Чему равна работа газа при изохорном переходе системы из состояния с давлением
1 кПа в состояние с давлением 3 кПа?
а/ 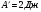 б/
б/ 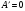
 в/
в/ 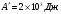
3.Изменится ли внутренняя энергия газа при его изотермическом расширении?
а/ увеличится б/ уменьшится в/ не изменится.
4.Какая из приведённых ниже формул позволяет рассчитать работу газа при изобарном процессе?
а/ 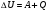 б/
б/ 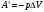
 в/
в/ 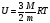
5.Внутрення энергия идеального одноатомного газа некоторой массы….
а/ зависит только от температуры б/ зависит только от объёма
в/ зависит от температуры и объёма
6.В процессе адиабатического расширения газ совершает работу, равную 3 кДж. Чему равно изменение внутренней энергии газа?
а/ 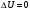 б/
б/ 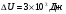 в/
в/ 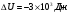
3. Решение задач.
Формулировка 1 закона термодинамики для случаев, если:
а/работа совершается над газом ΔU=Q+А
б/газ сам совершает работу ΔU=Q-А
Задача.1. На графике показан процесс расширения газа, который сопровождался уменьшением давления. На каком из участков графика работа газа была наибольшей?
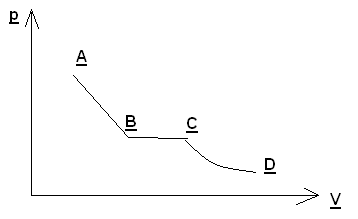
1) АВ 2) ВС 3) CD 4) одинаково
Решение: на графике зависимости давления газа от его объема работа газа численно равна площади фигуры под графиком. Максимальная площадь будет под участком АВ.
Ответ: 1
Задача 2. Аргон, находящийся в сосуде объемом 5 л, нагревают так, что его давление возрастает с 100 кПа до 300 кПа. Какое количество теплоты получил газ?
1) 1 кДж 2) 1,5 кДж 3) 2 кДж 4) 2,5 кДж
Решение: по первому закону термодинамики:
Q = ΔU + А
Так как процесс в закрытом сосуде является изохорным, то А = 0.
Q = ΔU = 3/2(р2V – р1V)
Переводя в систему СИ 100 кПа = 105 Па, 300 кПа = 3.105 Па, 5 л = 5.10-3 м3 и подставляя численные значения в формулу, получаем Q = 1500 Дж = 1,5 кДж.
Ответ: 2
Задача 3. На каком из графиков показан процесс изохорного охлаждения газа?
1) 2) 3) 4)
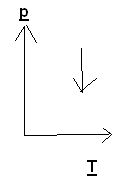
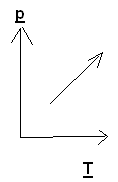
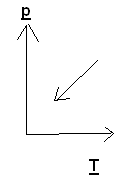
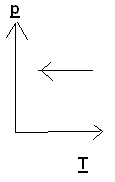
Решение: изохорный процесс – это процесс, протекающий при постоянном объеме. Изохорное охлаждение предполагает уменьшение температуры газа, что соответствует графику 3.
Ответ: 3
Задача 4. Газ получил количество теплоты, равное 1 кДж, и его сжали, совершив при этом работу 600 Дж. Как при этом изменилась внутренняя энергия газа?
1) увеличилась на 1600 Дж 2) увеличилась на 400 Дж
3) уменьшилась на 400 Дж 4) не изменилась
Решение: по 1-му закону термодинамики:
Q = ΔU + A,
ΔU = Q – А.
Так как газ сжимают, то работа газа будет отрицательной: – 600 Дж. Подставляя численные значения в формулу и переводя 1 кДж = 1000 Дж, получаем:
ΔU = 1600 Дж.
Ответ: 1
Задача 5.
Какую работу совершил газ, взятый в количестве двух молей при изобарном нагревании на 50 градусов Кельвина и как при этом изменилась их внутренняя энергия?
Решение:
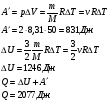
Ответ: 2077 Дж.
Задача 6. Во время расширения газа, вызванного его нагреванием, в цилиндре с площадью поперечного сечения S = 200 см2 газу было передано количество теплоты Q = 1,5 • 105 Дж, причём давление газа оставалось постоянным и равным р = 2 • 107 Па. На
сколько изменилась внутренняя энергия газа, если поршень передвинулся на расстояние Δh = 30 см?
Решение. Согласно первому закону термодинамики в форме Q = ΔU + А', где А' = pSΔh — работа, совершённая газом. Отсюда ΔU = Q - pSΔh = 30 кДж.
Ответ: 30 кДж.
Задача 7. Пусть азот нагревается при постоянном давлении. Зная, что масса азота m = 280 г, количество затраченной теплоты Q = 600 Дж и удельная теплоёмкость азота при постоянном объёме cv = 745 Дж/(кг • К), определите, на сколько повысилась температура азота. Молярная масса азота М = 0,028 кг/моль.
Решение. Согласно первому закону термодинамики Q = ΔU + А'.
Изменение внутренней энергии ΔU = cvmΔT.
Работа при изобарном процессе А' = pΔV = (m/M)RΔT.
Следовательно, Q = mΔT(cv + R/M), откуда
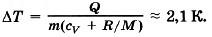 Ответ: 2,1К.
Ответ: 2,1К.
Задача 8. Идеальный газ, масса которого т и молярная масса μ, расширяется изобарно при некотором давлении. Начальная температура газа Т1, конечная Т2. Определить работу, совершаемую газом.
Решение:
Работа в изобарном процессе
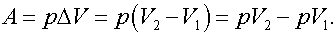
Из уравнения Менделеева—Клапейрона
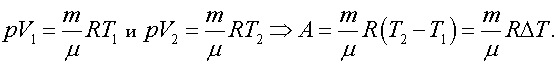
Оказалось, что работу в изобарном процессе можно выразить не только через изменение объема по формуле 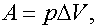 но и через изменение температуры:
но и через изменение температуры: 
.
Ответ: 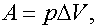

4. Домашнее задание. Решите задачи.
Задача 1. Газ находится в сосуде под давлением 2,5·104Па. При сообщении ему количества теплоты 6·104Дж он изобарно расширяется на 2м3. На сколько изменилась внутренняя энергия? Как изменилась его температура?
(Ответ: ∆U= ∆U– А = Q- р·∆V= 104 Дж; ∆T 0, т.к. ∆U 0)
Задача 2. Какова внутренняя энергия гелия, заполняющего аэростат объёмом 50 м3 при давлении 80 кПа?
Дано: “СИ” Решение.
V = 50 м3
р = 80 кПа =8∙104 Па
U - ?
Ответ: 6 МДж.






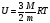 б/
б/ 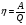 в/
в/ 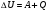

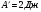 б/
б/ 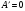
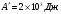
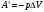
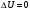 б/
б/ 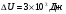 в/
в/