«Не в том суть жизни что в ней есть, но в вере в то, что в ней должно быть»
И. Бродский
Роль геометрии в школьном образовании
Геометрия является очень мощным средством развития личности в самом широком диапазоне. Среди дисциплин математического цикла геометрия выделяется своим вольнодумством, неким особым свободолюбивым характером, нежелающем подчиняться стандартам, нормам, алгоритмам.
В последнее время внимание ученых математиков и специалистов в области математического образования все больше и больше привлекает Элементарная геометрия.
Целью изучения геометрии, конечно, является знание. Но нужно всегда помнить, что геометрия есть феномен общечеловеческой культуры. Человек не может развиваться культурно и духовно, если он не изучал в школе геометрию. Геометрия возникла не только из практических, но и из духовных потребностей человека. Именно в геометрии особо заметен евразийский характер русской культуры. В истории геометрии ярко видны две ветви: западная и восточная. Западная геометрия строилась по Евклиду, а затем по Декарту. Здесь во главу ставились точные логические конструкции, систематичность, общие теории. Восточная геометрия опиралась на наглядность. Она была скорее элементом культуры, искусства, нежели наукой. И эти две ветви тесно переплелись в России, географически и геометрически служившей мостом между Западом и Востоком.
Научной и нравственной основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений.
Геометрия, впрочем, как и алгебра, является носителем собственного познания мира. Овладение этим методом – важнейшая цель образования. Процесс изучения геометрии должен включать самые разнообразные виды деятельности. В том числе и даже в первую очередь – решение задач. Задача – это не только умения, это и элемент знания. Ученик должен ознакомиться с определенным набором достаточно трудных геометрических задач, научиться решать задачи, следуя известным образцам. В геометрии в отличие от алгебры алгоритмов очень мало, почти нет. Поэтому при обучении возрастает значение опорных задач, обобщающих полезный факт, либо иллюстрирующий метод или прием.
Как сказал И.Ф. Шарыгин «Геометрия должна быть геометрической». Это означает, что главным действующим лицом геометрии должна быть фигура, а главным средством обучения рисунок, чертеж.
§ 1. Требования к чертежу
Решение любой геометрической задачи начинается с чертежа. Рассмотрим основные требования к чертежу:
чертеж должен быть аккуратно выполненным и достаточно большим. Это не означает, что его нужно выполнять с помощью чертежных инструментов. При небольшом навыке чертеж может быть хорошо выполнен и от руки.
Чертеж должен быть «лаконичным», то есть следует изображать «функционирующие» части геометрических фигур. Так, если надо найти радиус окружности, то в большинстве случаев саму эту окружность не следует изображать. Иногда полезно делать выносные чертежи, изображая фрагмент общей конфигурации.
Иногда полезно делать два чертежа. Первый – правильный, с помощью которого можно сделать геометрические открытия: увидеть, что точки лежат на одной прямой или одной окружности, или прямые пересекаются в одной точке; второй – неправильный, для проведения доказательства.
если в задаче идет речь о фигуре общего вида, то необходимо, чтобы на изображении фигура не имела характерных особенностей фигур частного вида: например, произвольный треугольник не должен быть изображен равнобедренным, прямоугольным или правильным, произвольный четырехугольник - параллелограммом.
§2. Метод дополнительных построений
Одним из эффективных методов решения геометрических задач является метод дополнительных построений. Дополнительные построения позволяют свести задачу к задачам, решения которых хорошо известны или легко могут быть получены. Требуется большой опыт, изобретательность, геометрическая интуиция, чтоб догадаться, какие дополнительные линии следует провести. Иногда условие задачи подсказывает выбор дополнительного построения.
Так практика показывает, что полезно в трапеции провести через одну вершину прямую, параллельную противоположной боковой стороне; если речь в задаче идет о диагоналях, то дополнительное построение состоит в проведении через одну из ее вершин прямой, параллельной диагонали.
Если в условии говорится о медиане треугольника, то стоит попытаться продолжить эту медиану на такое же расстояние.
Если в задаче фигурирует середина одной или нескольких сторон четырехугольника, то стоит добавить середины каких-то других сторон или диагоналей и рассмотреть средние линии соответствующих треугольников. Этот прием называют методом «средних линий».
Таким образом, выделены три разновидности дополнительных построений:
продолжение отрезка на определенное расстояние или до пересечения с заданной прямой;
проведение прямой через две заданные точки;
проведение через заданную точку прямой, параллельной данной прямой.
При решении геометрических задач также применяют метод вспомогательной фигуры, например « вспомогательного треугольника». При помощи некоторого дополнительного построения (продление отрезка, геометрическое преобразование и др.) получают треугольник, который дает возможность получить решение задачи. Обычно такой треугольник обладает двумя важными для решения задачи свойствами:
1) его элементы некоторым образом связаны с элементами, фигурирующими в условии задачи;
2) для его элементов легче найти характеристики, позволяющие получить решение, чем для фигур непосредственно заданных условием.
Рассмотрим конкретные примеры.
 Пример 1. Найти высоту равнобедренной трапеции, если ее диагонали взаимно-перпендикулярны и площадь равна S.
Пример 1. Найти высоту равнобедренной трапеции, если ее диагонали взаимно-перпендикулярны и площадь равна S.
Решение. Пусть в трапеции ABCD  ,
, 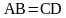 ,
, 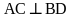 и площадь ABCD равна S (рис. 1). Через точку С проведем прямую параллельную диагонали BD. Е – точка пересечения ее с прямой AD. Рассмотрим треугольник АСЕ:
и площадь ABCD равна S (рис. 1). Через точку С проведем прямую параллельную диагонали BD. Е – точка пересечения ее с прямой AD. Рассмотрим треугольник АСЕ: 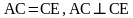 . СН – высота трапеции.
. СН – высота трапеции. 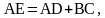
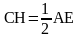 .
.
Следовательно,  ,то есть
,то есть 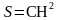 и
и  .
.
Пример 2. На сторонах треугольника АВС построены квадраты ABDE и BCKF. Доказать, что медиана ВМ равна половине DF.
 Решение. Продолжим медиану ВМ на отрезок MQ равный ВМ (рис. 2). Рассмотрим треугольники DBF и BCQ.
Решение. Продолжим медиану ВМ на отрезок MQ равный ВМ (рис. 2). Рассмотрим треугольники DBF и BCQ. 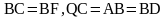
 ; Так как ABCQ – параллелограмм, то
; Так как ABCQ – параллелограмм, то  . Итак,
. Итак,  и
и 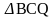 равен
равен  . Следовательно,
. Следовательно,  или
или 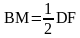 .
.
Пример 3. Расстояние между серединами двух противоположных сторон выпуклого четырехугольника равно полусумме двух других его сторон. Доказать, что этот четырехугольник трапеция.
Решение. Пусть М – середина АВ, N – середина CD четырехугольника ABCD (рис. 3). Проведем диагональ АС и обозначим точкой О середину АС.  Тогда МО – средняя линия
Тогда МО – средняя линия  , поэтому
, поэтому 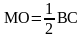 и
и  . ON – средняя линия
. ON – средняя линия  . Следовательно,
. Следовательно,  и
и  . По условию Так как то
. По условию Так как то  , что возможно, когда точки M, O, N лежат на одной прямой. Следовательно,
, что возможно, когда точки M, O, N лежат на одной прямой. Следовательно,  ,
,  . По свойству транзитивности
. По свойству транзитивности  , то есть ABCD – трапеция.
, то есть ABCD – трапеция.
 Пример 4. Доказать, что средние линии треугольника параллельны его сторонам и вдвое меньше их.
Пример 4. Доказать, что средние линии треугольника параллельны его сторонам и вдвое меньше их.
Решение. Пусть точки K, L, M – середины сторон AB, BC, CA треугольника ABC соответственно (см. рис.)
Продолжим отрезок KL за точку L на отрезок NL = KL и получим вспомогательный треугольник NLC. Тогда
∆ KBL = ∆ NC L (по двум сторонам и углу между ними). Поэтому BK = CN и  B =
B =  4. Следовательно, AK = CN (так как AK = KB и KB = CN) и AK || CN (так как
4. Следовательно, AK = CN (так как AK = KB и KB = CN) и AK || CN (так как  B =
B =  4). Поскольку AK = CN и AK || CN, то KN = AC и KN || AC. Поэтому
4). Поскольку AK = CN и AK || CN, то KN = AC и KN || AC. Поэтому  3 =
3 =  A,
A,  1 =
1 =  C и KL = 0,5AC. Значит, углы треугольника KBL равны углам треугольника ABC, а стороны его вдвое меньше сторон треугольника ABC. Это же верно и для треугольников AKM, MCL, KML, так как они равны треугольнику KBL.
C и KL = 0,5AC. Значит, углы треугольника KBL равны углам треугольника ABC, а стороны его вдвое меньше сторон треугольника ABC. Это же верно и для треугольников AKM, MCL, KML, так как они равны треугольнику KBL.
P.S. Кроме описанного метода, при решении данной задачи используется известное дополнительное построение – продление
отрезка на отрезок, равный самому себе.
Одним из дополнительных построений, дающих ключ к решению ряда задач, является проведение вспомогательной окружности. Использование в решении планиметрических задач такого дополнительного построения можно рассматривать как специальный метод решения этих задач – метод вспомогательной окружности.
Суть метода заключается в том, что при решении планиметрических задач, когда требуется установить связь между данными и искомыми величинами, нередко полезно около треугольника или четырехугольника описать окружность, после чего эти связи становятся более ощутимыми или даже очевидными.
Использование такого метода во многих случаях делает решение сложных задач очень простым, наглядным и практически устным.
При решении планиметрических задач успех во многом определяется удачным использованием того или иного метода решения. Но как определить, какой метод наиболее подходящий в том или ином случае?
Анализ решения достаточно большого круга задач показывает, что использование вспомогательной окружности связано с характерными признаками фигуры, рассматриваемой в задаче.
Целесообразность применения метода зависит от этих признаков. А они основаны на теоремах и их следствиях, изучаемых в курсе геометрии 8,9 классов. Напомним их:
1) Вписанный угол измеряется половиной дуги, на которую он опирается.
2) Вписанные углы, опирающиеся на одну и ту же дугу, равны.
3) Вписанный угол, опирающийся на полуокружность, прямой.
4) Угол с вершиной внутри круга измеряется полусуммой двух дуг, одна из которых расположена внутри этого угла, а другая – внутри угла, вертикального к данному.
5) Угол, вершина которого расположена вне круга, а каждая из сторон пересекает окружность в двух точках, измеряется полуразностью дуг, заключенного внутри угла.
6) Угол между касательной к окружности и хордой, проведенной через точку касания, измеряется половиной дуги, заключенной внутри этого угла.
7) В любой треугольник можно вписать окружность и притом единственную.
8) Около любого треугольника можно описать единственную окружность.
9) Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность, центр которой – точка пересечения диагоналей.
10) Около трапеции можно описать окружность только тогда, когда она равнобочная.
В процессе изучения метода вспомогательной окружности необходимо научиться выделять и использовать те признаки, наличие которых в задаче приводит к построению вспомогательной окружности и с ее помощью устанавливать связи между необходимыми объектами и величинами, определенными условием задачи. Тем более, что задачи на использование метода вспомогательной окружности – частые гости на ЕГЭ и на экзаменах по геометрии за курс основной школы.
Вот эти признаки.
1) Если дан правильный треугольник, то можно провести окружность с центром в любой из его вершин и радиусом, равным длине его стороны, либо описать около него окружность, которая разобьется вершинами треугольника на равные дуги по 1200 каждая.
2) Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы, а радиус равен медиане, проведенной к гипотенузе этого треугольника.
3) Если удается установить, что суммы противоположных углов выпуклого четырехугольника равны, то вокруг него описывается окружность.
4) Если дан квадрат, прямоугольник или равнобедренная трапеция, то вокруг них описывается окружность.
5)Пусть около треугольника АВС описана окружность с центром О. Если точки О и С лежат по одну сторону от прямой АВ, то согласно свойству
вписанного и центрального углов ; если же эти точки лежат по разные стороны от АВ, то . Обратно, если: 1) точки О и С лежат по одну сторону от АВ,  и или 2) точки О и С лежат по разные стороны от АВ,
и или 2) точки О и С лежат по разные стороны от АВ,  и , то точка О – центр окружности, описанной около треугольника АВС.
и , то точка О – центр окружности, описанной около треугольника АВС.
 6) При определенных условиях окружность можно описать и около четырехугольника. Если четырехугольник ABCD вписан в окружность, то сумма его противоположных углов равна 1800, а углы ABD и ACD, опирающиеся на одну и туже дугу, равны (рис. 4). Верно и обратное предложение.
6) При определенных условиях окружность можно описать и около четырехугольника. Если четырехугольник ABCD вписан в окружность, то сумма его противоположных углов равна 1800, а углы ABD и ACD, опирающиеся на одну и туже дугу, равны (рис. 4). Верно и обратное предложение.
Точки A, B, C, D лежат на одной окружности, если: 1) ABCD – выпуклый четырехугольник и сумма его противоположных углов равна 1800 или 2) точки В и С лежат по одну сторону от прямой AD и  (то есть отрезок AD виден из точек В и С под равными углами).
(то есть отрезок AD виден из точек В и С под равными углами).
Применяя перечисленные свойства, легко решить следующую полезную задачу.
 Пример 5. В остроугольном треугольнике АВС проведены высоты АА1, ВВ1, СС1. Пусть Н – точка пересечения высот. Постройте треугольник А1В1С1 и перечислите все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 5).
Пример 5. В остроугольном треугольнике АВС проведены высоты АА1, ВВ1, СС1. Пусть Н – точка пересечения высот. Постройте треугольник А1В1С1 и перечислите все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 5).
Ответ.  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
P.S. Обоснуйте ответ, используя вышеперечисленные свойства.
Рассмотрим задачи решаемые данным методом.
Пример 6. В остроугольном треугольнике АВС проведены высоты  и
и  . Доказать, что треугольник
. Доказать, что треугольник  подобен данному треугольнику АВС с коэффициентом подобия, равным
подобен данному треугольнику АВС с коэффициентом подобия, равным  .
.
 Решение. На стороне АС треугольника АВС как на диаметре опишем полуокружность, которая пройдет через основания высот
Решение. На стороне АС треугольника АВС как на диаметре опишем полуокружность, которая пройдет через основания высот  и
и  (рис. 6). Так как четырехугольник
(рис. 6). Так как четырехугольник  вписанный, то . Следовательно, и . Так как стороны
вписанный, то . Следовательно, и . Так как стороны  и
и  являются соответствующими сторонами в подобных треугольниках, то их отношение
являются соответствующими сторонами в подобных треугольниках, то их отношение  равно коэффициенту подобия. Но в прямоугольном треугольнике
равно коэффициенту подобия. Но в прямоугольном треугольнике  . Итак, и
. Итак, и  .
.
Пример 7. Через некоторую точку плоскости проведены три прямые так, что угол между любыми двумя из них равен 600.Докажите, что основания перпендикуляров, опущенных из любой точки плоскости на эти прямые, служат вершинами равностороннего треугольника.
 Решение. Пусть три данные прямые пересекаются в точке О; М – произвольная точка плоскости; А, В, и С основания перпендикуляров, опущенных из точки М на данные прямые (рис. 7). Точки О, М, А, В и С лежат на одной окружности с диаметром ОМ (обоснуйте это). Теперь видно, что
Решение. Пусть три данные прямые пересекаются в точке О; М – произвольная точка плоскости; А, В, и С основания перпендикуляров, опущенных из точки М на данные прямые (рис. 7). Точки О, М, А, В и С лежат на одной окружности с диаметром ОМ (обоснуйте это). Теперь видно, что  , поскольку оба они опираются на одну и туже дугу
, поскольку оба они опираются на одну и туже дугу  . Значит,
. Значит,  . Точно так же , то есть треугольник АВС равносторонний.
. Точно так же , то есть треугольник АВС равносторонний.
Пример 8. Медиана и высота треугольника, проведенные из одной вершины внутри него, различны и образуют равные углы со сторонами, выходящими из той же вершины. Доказать, что треугольник прямоугольный.
 Решение. Пусть высота СН и медиана СМ треугольника АВС образует со сторонами АС и ВС равные углы (рис. 8). Опишем около треугольника АВС окружность. Достаточно доказать, что АВ – ее диаметр. Продолжим медиану СМ до пересечения с окружностью в точке D и рассмотрим треугольники АСН и DCB. Так как
Решение. Пусть высота СН и медиана СМ треугольника АВС образует со сторонами АС и ВС равные углы (рис. 8). Опишем около треугольника АВС окружность. Достаточно доказать, что АВ – ее диаметр. Продолжим медиану СМ до пересечения с окружностью в точке D и рассмотрим треугольники АСН и DCB. Так как  по условию и
по условию и  как вписанные углы, опирающиеся на одну и ту же дугу, то . Следовательно,
как вписанные углы, опирающиеся на одну и ту же дугу, то . Следовательно,  диаметр окружности.
диаметр окружности.
Центр окружности лежит на диаметре  и на серединном перпендикуляре m к стороне АВ. Так как по условию CD не является высотой, то прямые m и
и на серединном перпендикуляре m к стороне АВ. Так как по условию CD не является высотой, то прямые m и  имеют только одну общую точку М, которая является центром описанной окружности. Следовательно, АВ – диаметр окружности и
имеют только одну общую точку М, которая является центром описанной окружности. Следовательно, АВ – диаметр окружности и  .
.
Пример 9. Доказать, что в произвольном треугольнике АВС имеет место зависимость  , где
, где  - биссектриса угла В, a, b, c стороны треугольника АВС, а1, с1 – отрезки на которые биссектриса
- биссектриса угла В, a, b, c стороны треугольника АВС, а1, с1 – отрезки на которые биссектриса  делит противоположную сторону.
делит противоположную сторону.
 Доказательство. Около треугольника АВС опишем окружность и продолжим биссектрису BD угла В до пересечения с окружностью в точке Е (рис. 9). Соединим точки Е и С. Положим
Доказательство. Около треугольника АВС опишем окружность и продолжим биссектрису BD угла В до пересечения с окружностью в точке Е (рис. 9). Соединим точки Е и С. Положим  .
.
По свойству пересекающихся хорд имеем:  (а)
(а)
Рассмотрим треугольника ABD и EBC.  по условию.
по условию.  как углы опирающиеся на одну и ту же дугу. Следовательно,
как углы опирающиеся на одну и ту же дугу. Следовательно,  . Из подобия треугольников имеем
. Из подобия треугольников имеем  (б).
(б).
Из условий (а) и (б) следует, что 
§ 3. Метод площадей
Метод площадей имеет много разновидностей. Его применяют, например, при замене отношения отрезков, расположенных на одной прямой, отношением площадей треугольников с общей вершиной, основаниями которых являются рассматриваемые отрезки. При решении задач используют следующие свойства площадей:
Свойство 1. Площадь фигуры является не отрицательным числом.
Свойство 2. Площади равных фигур равны.
Свойство 3. Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.
Фигуры, имеющие равные площади, называются равновеликими.
При решении задач методом площадей часто применяют основные формулы, выражающие площадь треугольника.
Обозначим, через А , В и С величины соответствующих углов треугольника АВС, а через а, b и с, как обычно, длины противолежащих им сторон, 2р – периметр треугольника, r и R – соответственно радиус вписанной и описанной окружности.
В этих обозначениях для площади треугольника справедливы следующие формулы:
(2.1)
(2.2)
(2.3)
 (3.4)
(3.4)
(2.5)
Формулы (1), (4) и (5) хорошо известны, формулы (2), (3) получаются из формулы (1), используя теорему синусов.
Используя формулу (1) для площади треугольника, можно доказать теорему о биссектрисе внутреннего угла треугольника.
Теорема. Если  – биссектриса угла А треугольника АВС, то
– биссектриса угла А треугольника АВС, то  .
.
 Доказательство. Пусть угол при вершине А в треугольнике АВС равен
Доказательство. Пусть угол при вершине А в треугольнике АВС равен  . Рассмотрим треугольники
. Рассмотрим треугольники  и
и  (рис. 10). Их площади относятся как отрезки
(рис. 10). Их площади относятся как отрезки  и
и  . Используя формулу (2.1) имеем .
. Используя формулу (2.1) имеем .
Рассмотрим опорные задачи, решаемые методом площадей.
 Пример 10. Пусть две прямые пересекаются в точке А. В и В1 – любые две точки на одной прямой, а С и С1 – на другой. Докажите, что .
Пример 10. Пусть две прямые пересекаются в точке А. В и В1 – любые две точки на одной прямой, а С и С1 – на другой. Докажите, что .
Решение. Углы при вершине А треугольников АВС и АВ1С1 либо равны, либо дополняют друг друга до  (рис. 11), то есть в любом случае синусы этих углов равны. Используя формулу (2.1) для площади треугольника имеем .
(рис. 11), то есть в любом случае синусы этих углов равны. Используя формулу (2.1) для площади треугольника имеем .
Пример11. На сторонах АВ и АС треугольника АВС взяты точки В1 и С1 так, что  ,
,  . Докажите, что
. Докажите, что  .
.
Решение следует непосредственно из предыдущего примера.
Пример 12. Докажите, что длину биссектрисы  треугольника АВС можно вычислить по формуле , где
треугольника АВС можно вычислить по формуле , где  ,
,  ,
,  , А – угол ВАС.
, А – угол ВАС.
 Решение. Учитывая свойство 3 площади, имеем
Решение. Учитывая свойство 3 площади, имеем  или . Заменив в левой части равенства
или . Заменив в левой части равенства  и сократив обе его части на
и сократив обе его части на  , получим , откуда .
, получим , откуда .
Рассмотрим еще одну полезную задачу.
Пример 13. Пусть О – точка пересечения диагоналей четырехугольника ABCD. Тогда имеет место равенство .
 Решение. Пусть
Решение. Пусть  и
и  высоты треугольников ABD и CBD, проведенные к стороне BD (рис. 13). Очевидно, что
высоты треугольников ABD и CBD, проведенные к стороне BD (рис. 13). Очевидно, что  . .
. .
Используя результаты предыдущих задач, рассмотрим еще один важный пример, который в учебнике И.Ф. Шарыгина «Геометрия. 7-9 классы» назван типичной задачей.
 Пример 14. В треугольнике АВС на сторонах АВ, ВС и СА взяты соответственно точки К, М и Р так, что АК:КВ=2:3, ВМ:МС=3:4, СР:АР=4:5. В каком отношении отрезок ВР делится отрезком КМ?
Пример 14. В треугольнике АВС на сторонах АВ, ВС и СА взяты соответственно точки К, М и Р так, что АК:КВ=2:3, ВМ:МС=3:4, СР:АР=4:5. В каком отношении отрезок ВР делится отрезком КМ?
Решение. Пусть ВР и КМ пересекаются в точке О (рис. 14) и  . Так как
. Так как  ,
,  , то . Так как
, то . Так как  ,
,  , то . Так как
, то . Так как  ,
,  , то . Следовательно, и .
, то . Следовательно, и .
При решении задач методом площадей следует помнить, что
Если отрезок, соединяющий вершину треугольника с точкой противоположной стороны делит треугольник на два равновеликих треугольника, то он является медианой.
Медианы треугольника делят его на шесть равновеликих треугольников.
Для произвольной точки М на медиане треугольника АВС, выходящей из вершины А справедливо, что треугольник АВМ и АМС равновелики.
Диагонали трапеции делят ее на четыре треугольника. Треугольники, прилежащие к боковым сторонам, равновелики.
5) Диагонали выпуклого четырехугольника делят его на четыре треугольника. Произведение площадей треугольников прилегающих к противоположным сторонам равны.
P.S.Докажите эти свойства.

3







 Пример 1. Найти высоту равнобедренной трапеции, если ее диагонали взаимно-перпендикулярны и площадь равна S.
Пример 1. Найти высоту равнобедренной трапеции, если ее диагонали взаимно-перпендикулярны и площадь равна S. ,
, 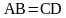 ,
, 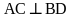 и площадь ABCD равна S (рис. 1). Через точку С проведем прямую параллельную диагонали BD. Е – точка пересечения ее с прямой AD. Рассмотрим треугольник АСЕ:
и площадь ABCD равна S (рис. 1). Через точку С проведем прямую параллельную диагонали BD. Е – точка пересечения ее с прямой AD. Рассмотрим треугольник АСЕ: 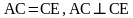 . СН – высота трапеции.
. СН – высота трапеции. 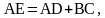
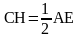 .
. ,то есть
,то есть 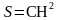 и
и  .
.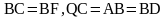
 ; Так как ABCQ – параллелограмм, то
; Так как ABCQ – параллелограмм, то  . Итак,
. Итак,  и
и 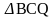 равен
равен  . Следовательно,
. Следовательно,  или
или 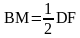 .
. , поэтому
, поэтому 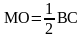 и
и  . ON – средняя линия
. ON – средняя линия  . Следовательно,
. Следовательно,  и
и