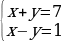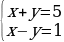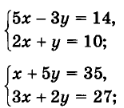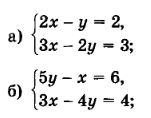Предмет: алгебра
Класс: 7
Тема урока: Система двух линейных уравнений с двумя переменными. Метод подстановки
Тип урока. Урок открытия нового знания.
Цели урока:
Обучающие (создание условий для формирования познавательных и логических УУД):
- углубление и систематизация теоретических знаний;
-закрепление навыков решения систем уравнений методом подстановки;
Развивающие (создание условий для формирования регулятивных УДД):
- развитие умения ставить перед собой цель, планировать свою работу;
- развитие логического мышления, памяти, внимания, умения сопоставлять, анализировать, делать выводы;
- развитие самостоятельности, потребности к самообразованию, к активной творческой деятельности;
Воспитательные (создание условий для формирования коммуникативных и личностных УДД):
- учиться работать с информацией, учиться работать в парах, развивать взаимовыручку, умение выслушать мнение товарищей, отстаивать свою точку зрения, учиться умению строить речевое высказывание в устной и письменной форме;
- воспитание чувства ответственности, культуры общения, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе.
Задачи урока
направленные на достижение предметных, метапредметных и личностных результатов:
-формирование умения работать с информацией по теме;
-формирование умения решать системы линейных уравнений с двумя неизвестными способом подстановки;
-формирование вычислительных навыков;
-формирование мотивации к учению и познанию;
-привитие интереса к предмету;
-формирование умения слушать, слышать, высказывать свое мнение, отстаивать свою точку зрения;
- формирование умения работать самостоятельно, в парах;
-формирование различных форм рефлексии.
- формирование умения строить речевое высказывание в устной и письменной форме;
- формирование чувства ответственности, культуры общения, уважения друг к другу
Оборудование к уроку: компьютер, мультимедийный проектор, раздаточный материал.
Структура урока:
1. Мотивация (самоопределение) к учебной деятельности.
2. Актуализация знаний.
3. Постановка проблемы.
4. Открытие нового знания.
5. Первичное закрепление.
6. Фронтальная работа с классом.
7. Работа в парах.
8. Самостоятельная работа.
9. Рефлексия.
10. Домашнее задание.
Математика сложна,
Но говорим с почтением,
Что математика нужна
Всем без исключения!
Ход урока.
1. Мотивация (самоопределение) к учебной деятельности.
Здравствуйте, ребята! Садитесь.
2. Актуализация знаний.
Какие системы уравнений вы видите на экране? (Линейные)
– Докажите, что данные системы линейные.
– Что является решением системы линейных уравнений?(Пара значений (х;у), которая одновременно является решением и первого, и второго уравнений системы).
– как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (графический).
– Алгоритм графического способа (1. Построить график каждого уравнения системы; 2. Найти координаты точки пересечения построенных прямых (если пересекаются)).
– Чем удобен графический метод? (для определения количества корней ситемы уравнений)
3. Постановка проблемы.
- Решите системы уравнений 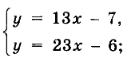 и
и 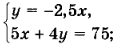 (работа в парах).
(работа в парах).
Задания делают на заранее приготовленных листах А4 с клетками, чтобы потом вывесить на доску, сравнить результаты и установить проблему урока
Вопросы учителя:
- Почему не решили систему уравнений? (Для решения данных систем уравнений графический способ не удобен. Не смогли построить графики).
- Почему? (Решением первой системы являются дробные числа, которые трудно определить по графику. Решением второй системы являются большие числа, для определения которых не достаточно тетради).
- Удобен ли известный нам способ решения системы линейных уравнений? ( Нет.)
- Какой выход вы предлагаете? ( Найти новый способ решения системы уравнений.)
- Какую цель мы перед собой поставим на этом уроке? ( Попробовать найти другой способ решения системы линейных уравнений.)
- Запишем тему урока «Система двух линейных уравнений с двумя переменными. Метод подстановки».
4.Открытие нового знания.
Для качественного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках.
№1.
Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)
(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)
7х-2у=0,
15х+3у=12
Ответ: у=3,5х у= 4 - 5х.
№2.
Вернемся в системе линейных уравнений из домашнего задания на сегодня:
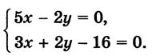
Вы ее решили графическим способом. А теперь решим эту систему другим способом.
Первое уравнение преобразуем к виду 2у = 5х, то есть у = 2,5 х. Второе уравнение преобразуем к виду 2у = 16 – 3х, затем у = 8 – 1,5х (все коэффициенты уравнения 2у = 16 – 3х разделили на 2). Теперь систему можно переписать:
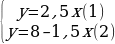
Значение у из (1) подставляем в (2) вместо у. Получаем уравнение 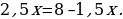 Получаем:
Получаем:
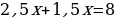
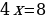
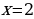
Если х = 2, то из уравнения у =2,5 х получим у = 5. Итак, (2;5) – решение системы.
- Дома так же получили единственное решение ? Совпадает? (Да).
№3. Решите систему линейных уравнений 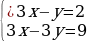 самостоятельно и попробуйте составить алгоритм по ключевым словам:
самостоятельно и попробуйте составить алгоритм по ключевым словам:
- выразим
- подставим
- решим
- подставим
- запишем.
После сверяем алгоритм по слайду. ( Ответ (-0,5; -3,5)).

- Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.
Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.
«Всеобщая арифметика», которая была издана в 1707 году.
5. Первичное закрепление.
Попробуем решить системы, которые вы решали в начале урока, но теперь методом подстановки:
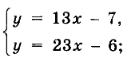 и
и 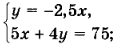
Кто может пойти к доске и выполнить это задание? (К доске …)
-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений - почему?
Странички истории.
Существует, ребята, еще один способ решения систем уравнений, который мы с вами еще не рассматривали. Это метод - метод перебора или подбора. Например, дается система:
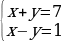
Можно легко подобрать значения х и у: х = 4, у = 3
-Попробуйте решить систему методом подбора:
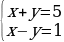
х = 3, у = 2
Все эти способы решения систем уравнений знали люди давно. Точной даты неизвестно, но они имеются в книге Ньютона
6. Фронтальная работа с классом.
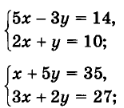
7. Работа в парах.
(по очереди объясняют решение уравнений друг другу)
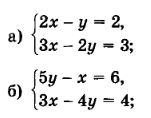
8. Самостоятельная работа.
1 вариант _ № 12.15 (а,в)

2 вариант _ № 12.16 (а,в)

9. Рефлексия. Оценки.
1) Какую цель мы поставили перед собой на этом уроке?
2) Почему она возникла?
3) Достигли ли мы своей цели?
На доске рисуется мишень, которая делится на сектора. В каждом из секторов записываются параметры- вопросы рефлексии состоявшейся деятельности. Участник ставит метки (стикеры или магниты) в сектора соответственно оценке результата: чем ближе к центру мишени, тем ближе к десятке, на краях мишени оценка ближе к нулю. Затем проводят её краткий анализ.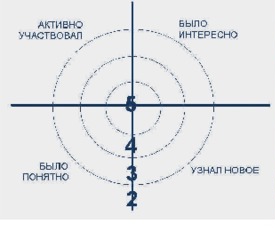
Оценки сегодня получили…
10. Домашнее задание.
Выучить(отработать) алгоритм решения системы линейных уравнений.
Самым трудным и важным делом для каждого ученика является выполнение домашнего задания. Если домашнее задание выполнено правильно, то на уроке вы чувствуете себя гораздо увереннее.
§12, № 12.14 , № 12.17
Спасибо за урок. До свидания.







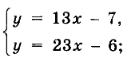 и
и 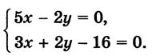
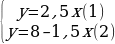
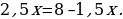 Получаем:
Получаем: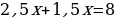
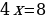
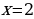
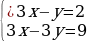 самостоятельно и попробуйте составить алгоритм по ключевым словам:
самостоятельно и попробуйте составить алгоритм по ключевым словам: