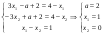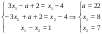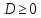Просмотр содержимого документа
«С6 подвижная галочка»
Подвижная галочка
2) Найти все зн р, при каждом из кот мн-во зн ф 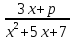 содерж полуинтерв(-1,3] . Опр при каждом таком р мн-во зн функции f(x) Отв: p=9,E(f)=[-1,3]
содерж полуинтерв(-1,3] . Опр при каждом таком р мн-во зн функции f(x) Отв: p=9,E(f)=[-1,3]
3) Найти все а, при кот Мн-во зн ф 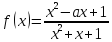 лежит на инт-ле (-3;3) отв -5a
лежит на инт-ле (-3;3) отв -5a
5) Найти все а, при каждом из кот фя 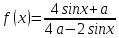 Приним все зн
Приним все зн
из промеж [0,1] Ответ -2aa
2)Найти все а, при кот нер-во 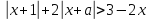 вып для любого х.
вып для любого х.
реш f(x)3 где 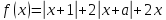
График f(x)- ломаная из частей прямых. Т 1 и a явл т излома, поэтому в них f(x)=min
 Ответ: [-2,4; 0]
Ответ: [-2,4; 0]
3) При каких зн а уравн 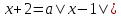 имеет единств решение? Найдите это рещ
имеет единств решение? Найдите это рещ
Отв при a 11 ур имеет единств реш. 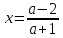
№19 Найди все зн а, при каждом из кот реш нер-ва |3x-a|+2
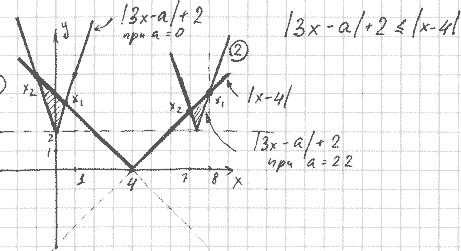
1)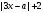 перес левую ветвь
перес левую ветвь 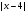 2)
2) 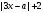 перес правую ветвь
перес правую ветвь 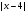
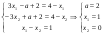
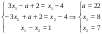
Это все. Такое м.быть при 2 знач параметра a=2 и a=22
5) Найти все а, при каждом из кот ф 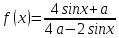 Приним все знач
Приним все знач
из промеж [0,1] Отв -2aa
507891 Найдите все зн а, при кот мн=во зн ф 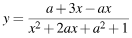 содержит отрезок [0,1]
содержит отрезок [0,1]
Реш 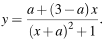 Отр [0,1] содерж в мн-ве зн данной ф т только, когда ур имеют решения.
Отр [0,1] содерж в мн-ве зн данной ф т только, когда ур имеют решения.
а)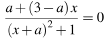 имеет реш при любом
имеет реш при любом 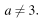 б)
б) 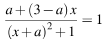 Ур
Ур 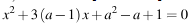
имеет реш т только тогда, когда 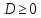
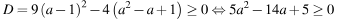
 откуда
откуда
№50) Найди все положит зн пар а, при каждом из кот уравн  имеет единст реш.
имеет единст реш.
Реш. Пусть  .Функ g(x) - непр, строго возр на всей обл опр и м приним любое зн в
.Функ g(x) - непр, строго возр на всей обл опр и м приним любое зн в При 0 Поэтому при любых таких a ур f(x) = g(x) имеет ровно 1 реш.(рис.1)
При 0 Поэтому при любых таких a ур f(x) = g(x) имеет ровно 1 реш.(рис.1)
При a = 1 f(x) =1, и ур f(x) = g(x) также имеет единств реш x=1.
При a 1:Производная функции  равна
равна  Приравн её к 0:
Приравн её к 0: 

 У произв единств 0. Слева от этого зн функция h(x) убывает, справа - возр. Поэтому она либо вообще не имеет 0, либо имеет два 0. И 1 корень она имеет только в том сл, когда он совп с найд экст. Т е, н найти такое a, при кот
У произв единств 0. Слева от этого зн функция h(x) убывает, справа - возр. Поэтому она либо вообще не имеет 0, либо имеет два 0. И 1 корень она имеет только в том сл, когда он совп с найд экст. Т е, н найти такое a, при кот  достиг экстр и обращ в 0 в одной и той же точке. Т е, когда прямая y=x явл касат к графику ф .
достиг экстр и обращ в 0 в одной и той же точке. Т е, когда прямая y=x явл касат к графику ф . (рис.2)
(рис.2)
Т е 
 Подст во 2е ур: x*ln(a) = 1, откуда ln(a)=1/x,
Подст во 2е ур: x*ln(a) = 1, откуда ln(a)=1/x, 
в 1е уравн: x = e. 
 отв (0;1] и {e(1/e)}
отв (0;1] и {e(1/e)}







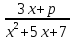 содерж полуинтерв(-1,3] . Опр при каждом таком р мн-во зн функции f(x) Отв: p=9,E(f)=[-1,3]
содерж полуинтерв(-1,3] . Опр при каждом таком р мн-во зн функции f(x) Отв: p=9,E(f)=[-1,3]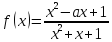 лежит на инт-ле (-3;3) отв -5a
лежит на инт-ле (-3;3) отв -5a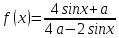 Приним все зн
Приним все зн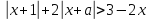 вып для любого х.
вып для любого х.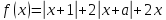
 Ответ: [-2,4; 0]
Ответ: [-2,4; 0] 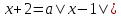 имеет единств решение? Найдите это рещ
имеет единств решение? Найдите это рещ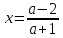

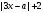 перес левую ветвь
перес левую ветвь 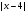 2)
2)