Самостоятельная работа по теме "Повторение: многогранники, сечения многогранников"

Самостоятельная работа

по теме «Повторение: многогранники, сечения многогранников»

Вариант для базового уровня

1. Постройте сечение куба плоскостью проходящей через точки М, N, P.

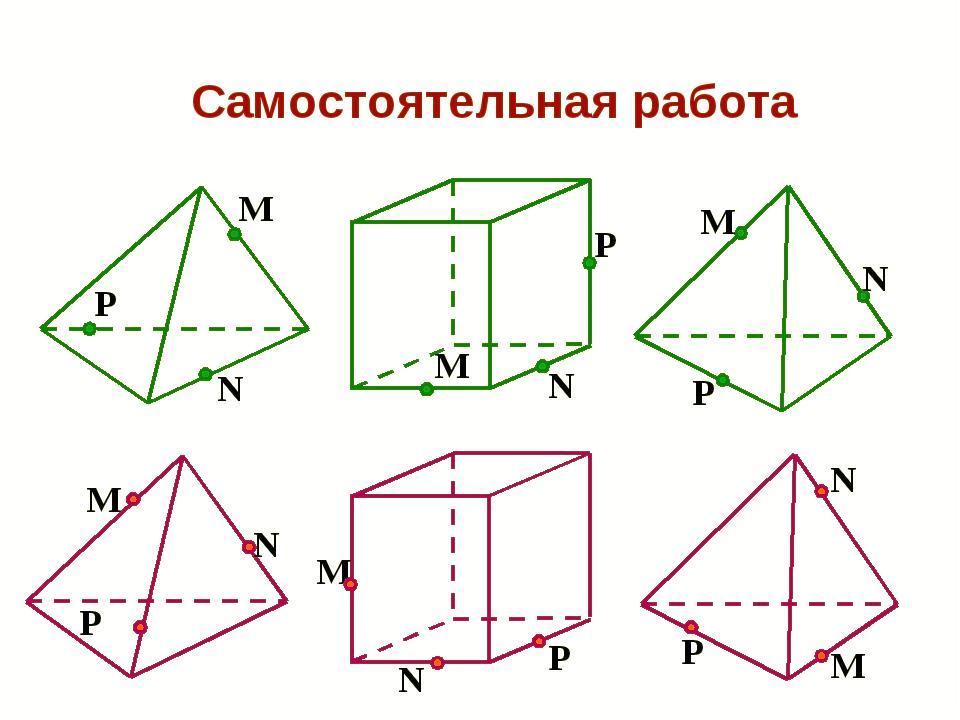2. Постройте сечение тетраэдра DABC плоскостью, проходящей через точки P, M, K, где P 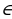AD, M BD и K BC, причем AP = PD, DM = MB.

3. В параллелепипеде ABCDA₁B₁C₁D₁ основание ABCD — квадрат со стороной, равной 8 см, остальные грани — прямоугольники. Боковое ребро равно 3 см, Е — середина А₁В₁. Постройте сечение параллелепипеда плоскостью, проходящей через АС и точку Е, и найдите периметр сечения.

Вариант для профильного уровня

1. Постройте сечение тетраэдра DABC плоскостью, проходящей через точки P, M, K, где P AD, M BD и K BC, причем AP = PD, DM = MB.

2. В параллелепипеде ABCDA₁B₁C₁D₁ основание ABCD — квадрат со стороной, равной 8 см, остальные грани — прямоугольники. Боковое ребро равно 3 см, Е — середина А₁В₁. Постройте сечение параллелепипеда плоскостью, проходящей через АС и точку Е, и найдите периметр сечения.

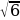3. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB равна 3, а боковое ребро АА₁ = . На рёбрах AB, A₁D₁ и C₁D₁ отмечены точки M, N и K соответственно, причём AM  =  A₁N  =  C₁K  =  1. Пусть L  — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL  — квадрат.