Самостоятельная работа № 2 по теме: «Векторы в пространстве. Подобие»
I вариант
1. (2 б.) Даны точки А (3; – 1; 2) и В (5; 1; 1). Найдите:
а) координаты вектора 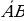 ; б)
; б)  .
.
2. (2 б.) Даны векторы  (– 2; 3; 1) и
(– 2; 3; 1) и  (4; – 1; 2). Найдите:
(4; – 1; 2). Найдите:
а) координаты вектора 2 –
–  ;
;
б) при каком значении у и z вектор 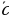 (8; у; z) и вектор
(8; у; z) и вектор  коллинеарны?
коллинеарны?
3. (2 б.) Найдите скалярное произведение векторов  и
и  , если:
, если:


а)  (2; – 4; 1),
(2; – 4; 1),  (3; 2; – 1); б)
(3; 2; – 1); б)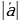 = 3,
= 3, 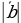 = 4, cos
= 4, cos 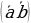 =
= 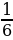 .
.
4. (2 б.) Найдите значение m, при котором векторы  и
и  перпендикулярны, если
перпендикулярны, если  (2; – 4; m),
(2; – 4; m),
 (3; – 1; 5).
(3; – 1; 5).
5. (2 б.) Найдите cos между векторами  (2; 3; – 1) и
(2; 3; – 1) и  (3; – 1; 2).
(3; – 1; 2).
6. (2 б.) В основании пирамиды лежит треугольник со сторонами 3 см, 4 см, 5 см. Через точку М, лежащую на высоте пирамиды, проведена плоскость параллельно основанию. В каком отношении точка М делит высоту пирамиды, если площадь сечения равна 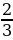 см2?
см2?
Самостоятельная работа № 2 по теме: «Векторы в пространстве. Подобие»
II вариант
1. (2 б.) Даны точки А (3; – 1; 2) и В (5; 1; 1). Найдите:
а) координаты вектора 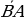 ; б)
; б) 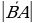 .
.
2. (2 б.) Даны векторы  (– 2; 3; 1) и
(– 2; 3; 1) и  (4; – 1; 2). Найдите:
(4; – 1; 2). Найдите:
а) координаты вектора  + 3
+ 3 ;
;
б) при каком значении у и z вектор 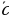 (8; у; z) и вектор
(8; у; z) и вектор  коллинеарны?
коллинеарны?
3. (2 б.) Найдите скалярное произведение векторов  и
и  , если:
, если:


а)  (– 2; 3; 1),
(– 2; 3; 1),  (– 1; – 1; 4); б)
(– 1; – 1; 4); б)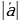 =2,
=2, 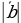 = 5, cos
= 5, cos 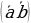 = 0,1.
= 0,1.
4. (2 б.) Найдите значение m, при котором векторы  и
и  перпендикулярны, если
перпендикулярны, если  (3; 2; – 1),
(3; 2; – 1),
 (2; m; – 2).
(2; m; – 2).
5. (2 б.) Найдите cos между векторами  (3; 2; – 1) и
(3; 2; – 1) и  (– 1; 2; 3).
(– 1; 2; 3).
6. (2 б.) В основании пирамиды лежит треугольник со сторонами 6 см, 8 см, 10 см. Через точку М, лежащую на высоте пирамиды, проведена плоскость параллельно основанию. В каком отношении точка М делит высоту пирамиды, если площадь сечения равна 6 см2?
Самостоятельная работа № 2 по теме: «Векторы в пространстве. Подобие»
III вариант
1. (2 б.) Даны точки А (3; – 1; 5) и В (4; 1; 3). Найдите:
а) координаты вектора 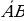 ; б)
; б)  .
.
2. (2 б.) Даны векторы  (3; – 4; 2) и
(3; – 4; 2) и  (– 2; 1; 6). Найдите:
(– 2; 1; 6). Найдите:
а) координаты вектора 2 +
+  ;
;
б) при каком значении х и у вектор 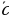 (х; у; 5) и вектор
(х; у; 5) и вектор  коллинеарны?
коллинеарны?
3. (2 б.) Найдите скалярное произведение векторов  и
и  , если:
, если:


а)  (3; – 1; 2),
(3; – 1; 2),  (2; 3; – 4); б)
(2; 3; – 4); б)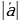 = 2,
= 2, 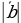 = 3, cos
= 3, cos 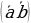 =
= 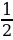 .
.
4. (2 б.) Найдите значение m, при котором векторы  и
и  перпендикулярны, если
перпендикулярны, если  (3; – 1; m),
(3; – 1; m),
 (2; 4; 3).
(2; 4; 3).
5. (2 б.) Найдите cos между векторами  (– 1; 2; 3) и
(– 1; 2; 3) и  (2; – 1; 3).
(2; – 1; 3).
6. (2 б.) В основании пирамиды лежит треугольник со сторонами 5 см, 12 см, 13 см. Через точку М, лежащую на высоте пирамиды, проведена плоскость параллельно основанию. В каком отношении точка М делит высоту пирамиды, если площадь сечения равна  см2?
см2?
Самостоятельная работа № 2 по теме: «Векторы в пространстве. Подобие»
IV вариант
1. (2 б.) Даны точки А (3; – 1; 5) и В (4; 1; 3). Найдите:
а) координаты вектора 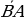 ; б)
; б) 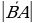 .
.
2. (2 б.) Даны векторы  (3; – 4; 2) и
(3; – 4; 2) и  (– 2; 1; 6). Найдите:
(– 2; 1; 6). Найдите:
а) координаты вектора  – 3
– 3 ;
;
б) при каком значении х и у вектор 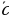 (х; у; 5) и вектор
(х; у; 5) и вектор  коллинеарны?
коллинеарны?
3. (2 б.) Найдите скалярное произведение векторов  и
и  , если:
, если:


а)  (1; – 2; 4),
(1; – 2; 4),  (2; – 1; 3); б)
(2; – 1; 3); б)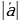 =5,
=5, 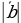 = 3, cos
= 3, cos 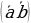 = 0,2.
= 0,2.
4. (2 б.) Найдите значение m, при котором векторы  и
и  перпендикулярны, если
перпендикулярны, если  (3; 2; – 1),
(3; 2; – 1),
 ( m; 3; 1).
( m; 3; 1).
5. (2 б.) Найдите cos между векторами  (3; – 1; 2) и
(3; – 1; 2) и  (3; 2; – 1).
(3; 2; – 1).
6. (2 б.) В основании пирамиды лежит треугольник со сторонами 10 см, 24 см, 26 см. Через точку М, лежащую на высоте пирамиды, проведена плоскость параллельно основанию. В каком отношении точка М делит высоту пирамиды, если площадь сечения равна 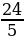 см2?
см2?







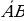 ; б)
; б)  .
. (– 2; 3; 1) и
(– 2; 3; 1) и  (4; – 1; 2). Найдите:
(4; – 1; 2). Найдите: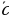 (8; у; z) и вектор
(8; у; z) и вектор 

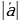 = 3,
= 3, 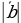 = 4, cos
= 4, cos 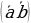 =
= 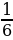 .
.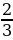 см2?
см2? 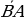 ; б)
; б) 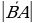 .
.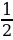 .
. см2?
см2? 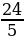 см2?
см2? 









