Самостоятельная работа 3.1
Свойства степени с натуральным показателем
Вариант 1
1. Записать выражение в виде одночлена стандартного вида:
а) 5 · (3mn) · (6m) в) 6 · (3kbc) · (- 5pkc)
б) 53ab2(-4)3ab г) 3ab7·4a9b2b
2. Записать одночлен в стандартном виде и найти его значение:
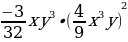 при х = -3, у = 2
при х = -3, у = 2
3. Возвести одночлен в степень:
а) (5b6)2 в) (2у10у)3
б) (–3а5 b)3 г) (–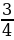 k6р3)2
k6р3)2
____________________________________________________________
4. Выполнить умножение одночленов:
(- 1,2a2b) · (-2ab2c)3 · (-abc4)
5. Записать одночлен в виде квадрата другого одночлена:
а) 1,44х8у12 б) 49a4b6
Самостоятельная работа 3.1
Свойства степени с натуральным показателем
Вариант 2
1. Записать выражение в виде одночлена стандартного вида:
а) 3 · (6ху) · (7х) в) 4 · (- 2mbc) · (- 8mkb)
б) 93a3b4(-8)3ab5 г) 6х2у5·3х9у2х
2. Записать одночлен в стандартном виде и найти его значение:
1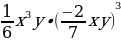 при х =
при х = 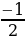 , у = -7
, у = -7
3. Возвести одночлен в степень:
а) (3а8)4 в) (4х10х)3
б) (–2b3)7 г) (–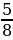 m4n5)2
m4n5)2
___________________________________________________________
4. Выполнить умножение одночленов:
(у5х2) · (-4х4у2z) · (-2,5ху7z4)4
5. Записать одночлен в виде квадрата другого одночлена:
а) 16х10у2 б) 1,96a12b4
Самостоятельная работа 3.2
Стандартный вид одночлена. Умножение одночленов
Вариант 1
1. Записать выражение в виде одночлена стандартного вида:
а) 5 · (3mn) · (6m) в) 6 · (3kbc) · (- 5pkc)
б) 53ab2(-4)3ab г) 3ab7·4a9b2b
2. Записать одночлен в стандартном виде и найти его значение:
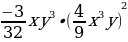 при х = -3, у = 2
при х = -3, у = 2
3. Возвести одночлен в степень:
а) (5b6)2 в) (2у10у)3
б) (–3а5 b)3 г) (–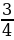 k6р3)2
k6р3)2
____________________________________________________________
4. Выполнить умножение одночленов:
(- 1,2a2b) · (-2ab2c)3 · (-abc4)
5. Записать одночлен в виде квадрата другого одночлена:
а) 1,44х8у12 б) 49a4b6
Самостоятельная работа 3.2
Стандартный вид одночлена. Умножение одночленов
Вариант 2
1. Записать выражение в виде одночлена стандартного вида:
а) 3 · (6ху) · (7х) в) 4 · (- 2mbc) · (- 8mkb)
б) 93a3b4(-8)3ab5 г) 6х2у5·3х9у2х
2. Записать одночлен в стандартном виде и найти его значение:
1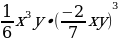 при х =
при х = 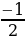 , у = -7
, у = -7
3. Возвести одночлен в степень:
а) (3а8)4 в) (4х10х)3
б) (–2b3)7 г) (–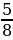 m4n5)2
m4n5)2
___________________________________________________________
4. Выполнить умножение одночленов:
(у5х2) · (-4х4у2z) · (-2,5ху7z4)4
5. Записать одночлен в виде квадрата другого одночлена:
а) 16х10у2 б) 1,96a12b4
Самостоятельная работа 3.3
Многочлены. Приведение подобных членов
Вариант 1
1. Привести многочлен к стандартному виду:
а) 2хх5·3у·(-3у) – 6х4·(-2у)
б) 4ab2 + 5b2а + bаа + 4a2b
в) 3а2 - 5а2 – 12а - 4а2 + 9а +14
2. Упростить многочлен и найти его значение:
а) 7a2b + 2аb2 – 5аb2 + 4ab2 + a2b, если а = 1, b = –0,2
б) –0,4х + 10x2у – 9x2у, если х = –3, y = 0,1
3. Приведите подобные члены и укажите степень многочлена:
а) 7с – 3а + 12d – 4b – 5а + 3b + 2d – 6с
б) 2х3 - 5x2у + 4x2y2 + 7x2у + 12х3 – 6хy2 - 8x2y2 + 4хy2
____________________________________________________________
4. Может ли при а0 и b0 значение многочлена:
а) 3а2b + ab + b2 + 2 быть числом положительным
б) b2 - 2а2 быть числом отрицательным?
Самостоятельная работа 3.3
Многочлены. Приведение подобных членов
Вариант 2
1. Привести многочлен к стандартному виду:
а) 3х6х·3у·(-2у) + 6х3· (-3у)
б) 4nm2 - 9n2m + mnm + 6m2n
в) 8b2 – 5b2 – 13b- 7b2 + 12b +35
2. Упростить многочлен и найти его значение:
а) –4a2b - 9ab2 - 2a2b + 5аb2 + 6a2b, если а = 3, b = –0,5
б) 0,2x + 12хy2 – 24хy2, если х = – 4, у = 0,1
3. Приведите подобные члены и укажите степень многочлена:
а) 12х– 3у + 4z + 5f – 4х – 17у + 9z – 3f
б) 7а4 + 15а3b + 3a2b2 – 8ab3 + 5а4 + 9a3b – 4a2b2 – 2ab3
____________________________________________________________
4. Может ли при а0 и b0 значение многочлена:
а) а2b – ab2 быть числом положительным
б) b2 + 2а2 + аb быть числом отрицательным?






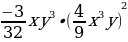 при х = -3, у = 2
при х = -3, у = 2 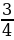 k6р3)2
k6р3)2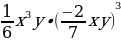 при х =
при х = 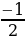 , у = -7
, у = -7 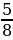 m4n5)2
m4n5)2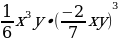 при х =
при х = 









