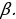САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
ПО ГЕОМЕТРИИ
7 КЛАСС
К учебнику Л.С. Атанасяна и др.
«Геометрия 7-9» (М.: Просвещение)
Составила: учитель математики Виноградова С.А.
Предлагаемый дидактический материал призван помочь учителю, работающему в 7 классах по учебнику Л.С. Атанасян и др. «Геометрия 7-9»
Предлагаемые задания удовлетворяют требованиям планируемых результатов обязательного уровня, содержат базовые задачи по всем темам геометрии за курс 7 класса. По каждому разделу предлагаются обучающие работы в 10 вариантах.
Использование большого количества задач по конкретной теме поможет учителю сформировать у учащегося устойчивые базовые навыки при решении опорных задач по геометрии и прежде всего – навыки самообразовательной деятельности ученика
ОБУЧАЮЩИЕ САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
ПО ГЕОМЕТРИИ
7 КЛАСС
Начальные геометрические сведения
Обучающая работа № 1: «Измерение отрезков»
Вариант 1
-
Точка М принадлежит отрезку DЕ, равному 54 см. Найдите длины отрезков DМ и ЕМ, если отрезок DМ в 8 раз меньше отрезка ЕМ.
-
Точка N лежит на прямой МК между точками М и К. Найдите расстояние между серединами отрезков МN и NК, если МN = 17 см, NК = 12 см.
-
Точки О, Р, К лежат на одной прямой. Известно, что ОК = 18 м. ОР – 7 м, РК = 11 м. Может ли точка К лежать между точками О и Р? Ответ обоснуйте.
Вариант 2
-
Точка М принадлежит отрезку ДЕ, равному 30 см. Найдите длины отрезков ДМ и ЕМ, если отрезок ДМ в 5 раз больше отрезка ЕМ.
-
Точка N лежит на прямой МК между точками М и К. Найдите расстояние между серединами отрезков МN и NК, если МN = 32 см, NК = 5 см.
-
Объясните, почему точки М, N и L не лежат на одной прямой, если МN = 8дм, М L = 5дм, NL = 6дм
Вариант 3
-
Точки М, Р и О принадлежат одной прямой, причём точки М и Р лежат по разные стороны от точки от точки О. Найдите длины отрезков ОМ и ОР, если МР = 28 см, а отрезок ОМ на 12 см короче отрезка ОР.
-
Точка D принадлежит отрезку ОМ. Найдите его длину, если ОD= 15 см, а DМ в 4 раза меньше, чем ОМ.
-
Точка А лежит на прямой ВС. Найдите длину отрезка АС, если АВ = 23м, ВС = 9м. Сколько решений имеет задача?
Вариант 4
-
Точка М, К и О принадлежат одной прямой, причём точки М и К лежат по разные стороны от точки О. Найдите длины отрезков ОМ и ОК, если МК = 48см, а отрезок ОМ на 4см длиннее отрезка ОК.
-
Точка D принадлежит отрезку ОМ. Найдите длину отрезка ОМ, если ОМ на 6см больше, чем DМ, а ОD =2ДМ.
-
Точка А лежит на прямой ВС. Найдите длину отрезка АС, если АВ = 19м, ВС = 11м. Сколько решений имеет задача?
Вариант 5
-
Точки М, Р и О принадлежат одной прямой. Причем точки М и Р лежат по разные стороны от точки О. Найдите длины отрезков ОМ и ОР, если МР = 35, и ОМ: ОР= 1: 6.
-
Точка D принадлежит отрезку ОА. Найдите его длину. Если ОD = 12 см, а АD на 5 см меньше, чем ОА.
-
Расстояние между точками А и В равно 8 см, а расстояние между точками В и С – 5 см. Может ли расстояние между А и С быть 13 см? Объясни почему.
Вариант 6
-
Точки К, Т и О принадлежат одной прямой. Причём точки К и Т лежат по разные стороны от точки О. Найдите длины отрезков КО и ОТ, если КТ = 36 и КО составляет 2/3 отрезка КТ
-
Точка О принадлежит отрезку ХУ. Найдите его длину, если ОУ = 20 см, а ОХ на 5 см меньше, чем ХУ.
-
Расстояние между точками В и С равно 3 см, а расстояние между точками В и D – 8см. Может ли расстояние между С и D быть 11 см? Объясни почему.
Вариант 7
-
Точки А, В, и С принадлежат прямой. Причём точки А и С лежат по разные стороны от точки В. Найти отрезок АС, если АВ = 10см, что составляет 1/5 отрезка АС.
-
Точка К принадлежит отрезку МN. Найдите его длину, если МК = 16 см, а КN составляет 40% отрезка МN.
-
Расстояние между точками К и Т равно 4 см, а расстояние между точками Т и N – 9см. Может ли расстояние между К и N быть 12 см? Объясни почему.
Вариант 8
-
Точки О принадлежит отрезку АВ, равному 24 см., причём точки А и В лежат по разные стороны от точки О. Найти длины отрезков АО и ОВ, если разность отрезков АО и ОВ составляет 12см.
-
Точка D принадлежит отрезку РК. Найдите его длину, если РD = 32 см, а DК составляет 1/5 отрезка МN.
-
Расстояние между точками N и М равно 11 см, а расстояние между точками М и Т на 3 см меньше. Может ли расстояние между N и Т быть 15 см? Объясни почему.
Вариант 9
-
Точка Е отрезка КD находится в 4 раза ближе к точке А, чем к точке D. Найдите КЕ и ЕД, если КD = 50см.
-
Точка М принадлежит отрезку АВ. Найдите его длину, если АМ = 42 см, а МВ составляет 2/3 отрезка АВ.
-
Точки А, В и С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС – 5 см, ВС = 7 см.? Объясни почему.
Вариант 10
-
Точки А, В, и С принадлежат прямой. Причём точки А и С лежат по разные стороны от точки В. ВС =30 см. Найти отрезок АС, если АВ равен 2/3 ВС.
-
Точки Х, У, С, D лежат на одной прямой. У – середина ХС, УС = 14 см, СD = 20 см. Найдите ХD.
-
Точки М, N, К и Р лежат на одной прямой. Найдите КР, если МN = 20 см, МК = 6 см, NР =8 см.
Обучающая работа № 2: «Измерение углов»
Вариант 1
-
Из точки М выходят три луча МР, МN, МК, причём луч МN проходит между сторонами угла РМК. Определите градусную меру угла РМК, если КМN = 40°, РМN в 3 раза больше КМN.
-
Луч m проходит между сторонами угла (bc). Найдите (bm) и (сm), если (bс) = 150°, (bm) в4 раза меньше, чем (сm).
-
Луч ОА проходит между сторонами угла ВОС. Найдите АОВ и АОС, если ВОС = 75° и АОВ на 13° меньше, чем АОС.
Вариант 2
-
Из точки М выходят три луча МР, МN, МК, причём луч МN проходит между сторонами угла РМК. Определите градусную меру угла РМК, если РМN = 110°, КМN на 50° меньше РМN.
-
Луч m проходит между сторонами угла (bc). Найдите (bm) и (сm), если (bс) = 80°, (bm) в 4 раза больше, чем (сm).
-
Луч ОА проходит между сторонами угла ВОС. Найдите АОВ и АОС, если ВОС = 148° и АОВ на 28° больше, чем АОС.
Вариант 3
-
Из точки О выходят три луча ОР, ОN, ОК, причём луч ОN проходит между сторонами угла РОК. Определите градусную меру угла РОК, если КОN = 120°, РОN в 3 раза меньше КОN.
-
Луч m проходит между сторонами угла (bc). Найдите (bm) и (сm), если (bс) = 75°, (bm) в 4 раза меньше, чем (сm).
-
Луч ОА проходит между сторонами угла ВОС. Найдите АОВ и АОС, если ВОС = 68° и АОС на 22° меньше, чем АОВ.
Вариант 4
-
Из точки О выходят три луча ОР, ОN, ОК, причём луч ОN проходит между сторонами угла РОК. Определите градусную меру угла РОК, если РОN = 20°, КОN на 20° больше РОN.
-
Луч m проходит между сторонами угла (bc). Найдите (bm) и (сm), если (bс) = 60°, (bm) в 5 раза больше, чем (сm).
-
Луч ОА проходит между сторонами угла ВОС. Найдите АОВ и АОС, если ВОС = 168° и АОС на 22° больше, чем АОВ.
Вариант 5
-
Из точки О выходят три луча ОА, ОВ, ОС, причём луч ОВ проходит между сторонами угла АОС. Определите градусную меру угла АОС, если АОС =150°, и АОВ: ВОС = 2: 3.
-
Луч n проходит между сторонами угла(ac). Найдите угол (nc), если угол (ас) = 160°, а разность углов (аn) и (nc) равна 40°.
3. Луч с – биссектриса (ab). Луч d - биссектриса (ac). Найдите (bd), если (ad)=80°.
Вариант 6
-
Из точки О выходят три луча ОА, ОВ, ОС, причём луч ОВ проходит между сторонами угла АОС. Определите градусную меру угла АОС, если АОС =160°, и
АО : ВОС = 1: 3.
-
Луч n проходит между сторонами развёрнутого угла (ac). Найдите угол (nc), если угол (аn) = 60°.
-
Луч с – биссектриса угла(ab). Луч d - биссектриса угла (ac). Найдите угол (bd), если угол (ad)=20°.
Вариант 7
-
Из точки О выходят три луча ОD, ОЕ, ОС, причём луч ОС проходит между сторонами угла АОС. Определите градусную меру угла АОС, если DОС =120°, и АОЕ составляет 2/3 угла DОС.
-
Луч p проходит между сторонами развёрнутого угла (ac). Найдите угол (nc), если угол (аn) = 60°.
-
Из вершины угла проведен луч, перпендикулярный его биссектрисе и образующий со стороной данного угла острый угол, равный 30°. Найдите величину данного угла.
Вариант 8
-
Из точки О выходят три луча ОD, ОЕ, ОС, причём луч ОС проходит между сторонами угла АОС. Определите градусную меру угла АОС, если DОЕ =80° и СОЕ составляет 1/4 угла DОЕ.
-
Луч k проходит между сторонами угла прямого угла (aс). Найдите угол (аk), если угол (kc) = 30°.
-
Из вершины угла, равного 80°, проведен луч, перпендикулярный биссектрисе угла. Какие углы образует этот луч со сторонами этого угла?
Вариант 9
-
Из точки С выходят три луча СD, СК, СМ, причём луч ОК проходит между сторонами угла ДСМ. Определите градусную меру угла ДСМ, если DСК =150°, что составляет 3/4 угла DСМ.
-
Луч k проходит между сторонами угла (ac). Найдите угол (kc), если угол (аk) = 60°, а сумма углов (аk) и (kc) равна 140°.
-
Луч с проходит между сторонами угла (ав), который равен 90°. Найдите углы (ас) и (вс), если угол (ас) в два раза больше угла (вс).
Вариант 10
-
Из точки С выходят три луча СD, СК, СМ, причём луч ОК является биссектрисой угла DСМ. Определите градусную меру угла DСМ, если DСК = 53°.
-
Луч p проходит между сторонами угла (ac). Найдите угол (pc), если угол (аp) =160°, а угол (pc) составляет 20% угла (аp).
-
Между сторонами угла (ав), который равен 80°, проходит луч с. Найдите угол (ас), если угол (св) в три раза меньше угла (ас).
Обучающая работа № 3: «Равные треугольники»
Вариант 1
-
Дано: ∆DВЕ = ∆АОС. Известно, что DЕ = 4,5 см, DВ = 9 см, D = 60°, В = 30°. Найдите соответствующие стороны и углы треугольника АОС.
-
На стороне ВС треугольника АВС взята точка D. Найдите длину отрезка ВD, если он на 5см короче, чем DС, а сторона ВС равна 18см.
Вариант 2
-
Дано: ∆АВС = ∆КОР. Известно, что КР = 2 см, О = 90°, К = 45°. Найдите соответствующие им стороны и углы треугольника АВС.
-
На стороне ВС треугольника АВС взята точка D. Найдите ВАD, если он в 2раза меньше, чем САD, а ВАС = 84°.
Вариант 3
-
Дано: ∆DВЕ = ∆МОС. Известно, что DЕ = 4,75 см, DВ = 9,5 см, D = 60°, Е = 90°. Найдите соответствующие стороны и углы треугольника МОК.
-
На стороне ВС треугольника АВС взята точка D. Найдите отрезок ВD, если он на 3 см длиннее, чем DС, а сторона ВС равна 13см.
Вариант 4
-
Дано: ∆НВМ = ∆КОР. Известно, что ОР = 2,4 см, РК = 1,2 см. О = 30°, К = 90°. Найдите соответствующие им стороны и углы треугольника НВМ.
-
На стороне ВС треугольника АВС взята точка D. Найдите ВАD, если он в 3 раза больше, чем САD, а ВАС = 75°.
Вариант 5
-
Дано: ∆АВС = ∆МКР, АВ = 9 см, ВС = 18 см, АС = 13 см. Найдите соответствующие стороны МКР.
-
На стороне АС треугольника АВС взята точка К. Найдите длину отрезка АК, если АК составляет 1/3 отрезка АС, а сторона АС = 18 см.
Вариант 6
-
Дано: ∆МNR = ∆ CTK, CT = 9 см, СК = 4 см, КСТ = 90°. Найдите соответствующие стороны и угол треугольника МNR.
-
На стороне АС треугольника АВС взята точка К. Найдите длину отрезка КС, если КС составляет 2/3 отрезка АК, а отрезок АК = 18 см.
Вариант 7
-
Дано: ∆СРК = ∆ МNR, КРС = 30°, РСК = 60°, РС = 8 см. Найдите соответствующие углы и сторону треугольника МNR.
-
На стороне АС треугольника АВС взята точка К. Найдите длину отрезка АК, если АК: КС=2:5 и АС= 21см.
Вариант 8
-
Дано: ∆АВР = ∆СDК, А = 30°, В= 40°, С=110°. Найдите соответствующие углы треугольника СDК.
-
На стороне АС треугольника АВС взята точка К. Найдите АВК, если АВК: КВС=2:3, а АВС=100°.
Вариант 9
-
Дано: ∆АОВ = ∆СМР, АО = 5см, ОВ = 8 см, М = 45°. Найдите соответствующие стороны и угол треугольников АОВ и СМР.
-
На стороне АС треугольника АВС взята точка К. Найдите КВС, если сумма углов АВК и КВС равна 120°, а угол АВК в 4 раза меньше угла КВС.
Вариант 10
-
Дано: ∆ РСD=∆ ХУZ, D = 65°, ХУ=9см, УZ=15см. Найдите соответствующие стороны и угол треугольников РСД и ХУZ.
-
На стороне АС треугольника АВС взята точка К. Найдите КВС, если угол АВС=150° а угол АВК составляет 30% угла АВС.
Обучающая работа № 4: «Смежные и вертикальные углы»
Вариант 1
-
Найдите углы, полученные при пересечении двух прямых, если один из углов равен 74°.
-
Найдите величины смежных углов, если один из них а 5 раз больше другого.
-
Найдите величину каждого из двух вертикальных углов, если их сумма равна 48°.
Вариант 2
-
Найдите углы, полученные при пересечении двух прямых, если один из углов равен 124°.
-
Чему равны смежные углы, если один из них на 30° меньше другого.
-
Найдите величину каждого из двух вертикальных углов, если их сумма равна 104°.
Вариант 3
-
Найдите величины всех углов, полученных при пересечении двух прямых, если сумма двух из них равна 164°.
-
Чему равны смежные углы, если один из них на 40° больше другого.
-
Какие из высказываний верны и какие неверны:
-
Если два угла вертикальные, то они равны.
-
Если два угла равны, то и вертикальные им углы равны.
-
Если два угла равны, то они вертикальные.
-
Если два угла с общей вершиной равны, то они вертикальные.
Ответ обоснуйте.
Вариант 4
-
Найдите величины всех углов, полученных при пересечении двух прямых, если разность двух из них равна 42°.
-
Найдите величины смежных углов, если один из них в 3 раза меньше другого.
-
Какие из высказываний верны и какие неверны:
-
Если два угла вертикальные, то они равны.
-
Если два угла равны, то и вертикальные им углы равны.
-
Если два угла с общей вершиной равны, то они вертикальные.
Ответ обоснуйте.
Вариант 5
-
Один из углов, которые получаются при пересечении двух прямых, равен 46°. Найдите остальные углы.
-
Градусные меры смежных углов относятся как 5:4. Какова градусная мера меньшего из этих углов?
-
Могут ли оба смежных угла быть острыми?
Вариант 6
-
Сумма трёх углов, полученных при пересечении двух прямых равна 265°. Найдите больший из углов.
-
Градусные меры смежных углов относятся как 2:3. Какова градусная мера большего из этих углов?
-
Верно ли утверждение: если два угла смежные, то один из них острый, а другой – тупой.
Вариант 7
-
Один из углов, которые получаются при пересечении двух прямых, равен сумме двух равных. Найти все полученные при пересечении углы.
-
Найти смежные углы (ао) и (ов), если угол (ао) меньше (ов) на 40°
-
Определите, являются ли два равных угла вертикальными, если они имеют общую вершину.
Вариант 8
-
Найдите 1, 2, 3, если 1 = 2+ 3
-
Найти смежные углы (ао) и (ов), если (ао) =3(ов).
-
Могут ли оба смежных угла быть острыми?
Вариант 9
-
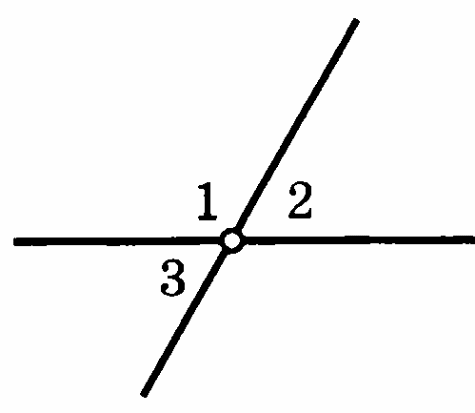
Найдите 3, 4, если 1 - 2 = 120°.
-
Найти смежные углы (ао) и (ов), если(ао) =1/2 (ов)
-
Определите, являются ли два угла вертикальными, если углы, смежные с ними, равны?
Вариант 10
-
Найдите 4, если 1 + 2 + 3 = 54

-
Найдите смежные углы. Если один из них на 20° меньше другого.
-
Верно ли утверждение: если два угла имеют общую сторону и их сумма равна 180°, то данные углы смежные?
Обучающая работа № 5: «Биссектриса угла»
-
Найдите угол между биссектрисой и стороной угла, равного 50°.
Вариант 2
-
Найдите угол, если его биссектриса образует с его стороной угол, равный 60°.
Вариант 3
-
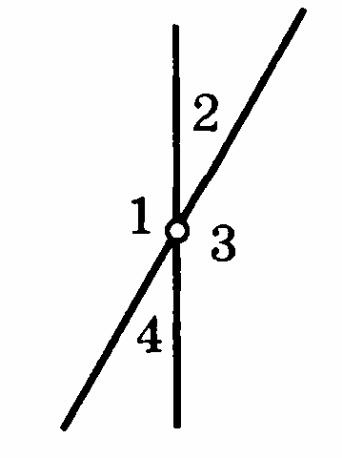
Дано: АВС=136°, СВD=3АВD. Найдите АВD и СВD.
Вариант 4
-
Дано: АВС=123°, АВD - СВD=17°. Найдите АВD и СВD.
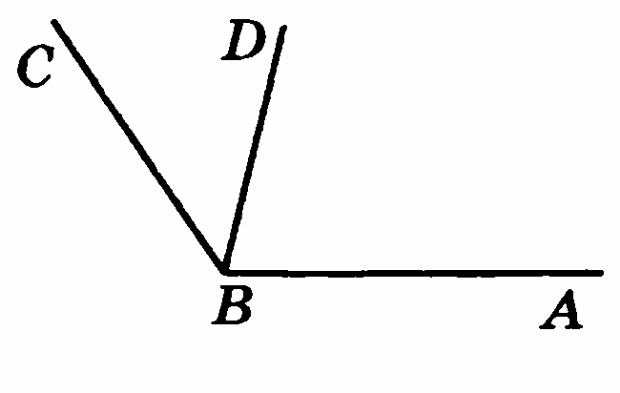
Вариант 5
-
Дано: ОВ – биссектриса угла АОС, ОС – биссектриса угла АОD. Найдите АОD.
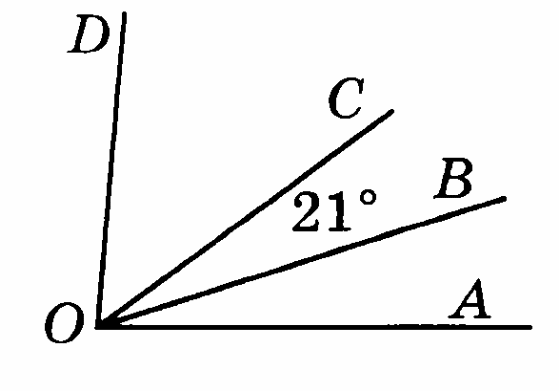
Вариант 6
-
Дано: АОС = 77°, АОВ: ВОС=2:5, ВОС – СОD = 12°. Найдите АОВ, ВОС, СОD.
Вариант 7
-
Дано: АОD = 126°, АОВ: ВОС: СОD = 1:3:2. Найдите АОВ, ВОС, СОD.
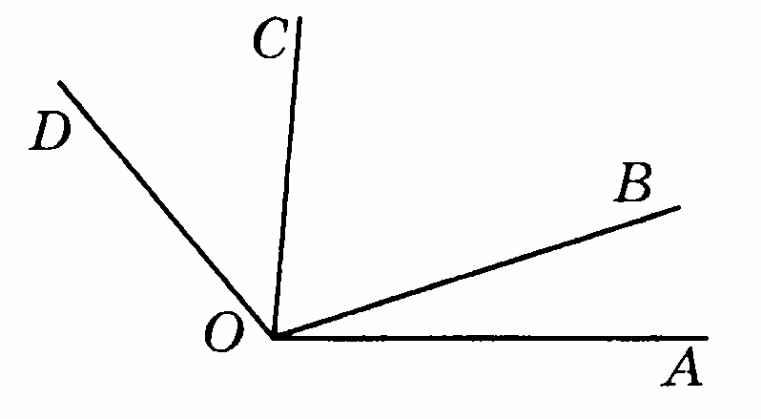
Вариант 8
-
Дано: АОВ = 123°, АОD = 98°, ВО СО Найдите СОD.
СО Найдите СОD.
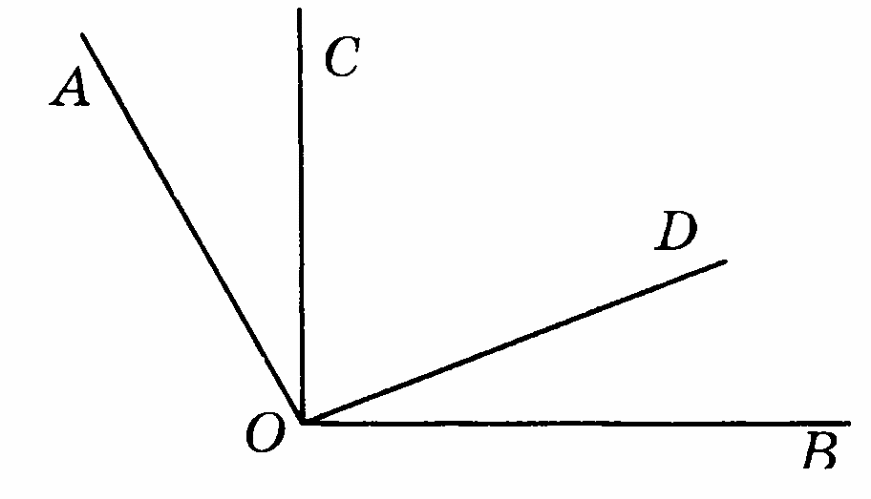
Вариант 9
-
Дано: ЕОD = 14°, АОЕ = 88°, ЕОD = СОD, АОВ = ВОС. Найдите АОВ.
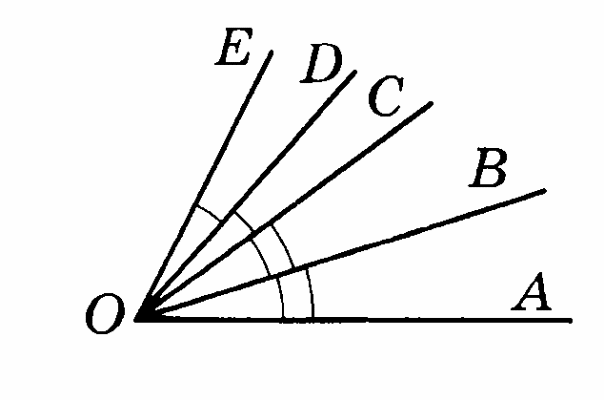
Вариант 10
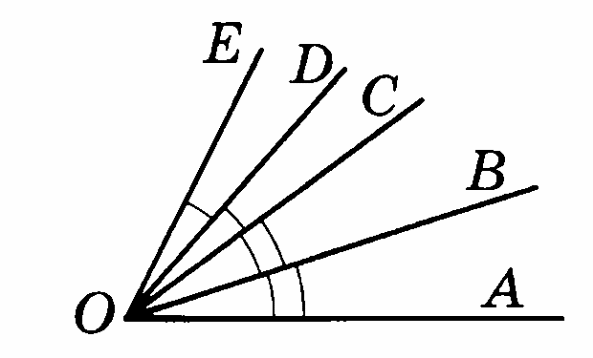
-
Дано: АОЕ = 60°, ВОС =17°, ЕОD = СОD, АОВ = ВОС. Найдите СОD.
Треугольники
Обучающая работа № 6: «Первый и второй признаки равенства треугольников»
Вариант 1
-
Луч ОР является биссектрисой угла КОМ. Докажите, что ∆КОР = ∆МОР, если ОК = ОМ.
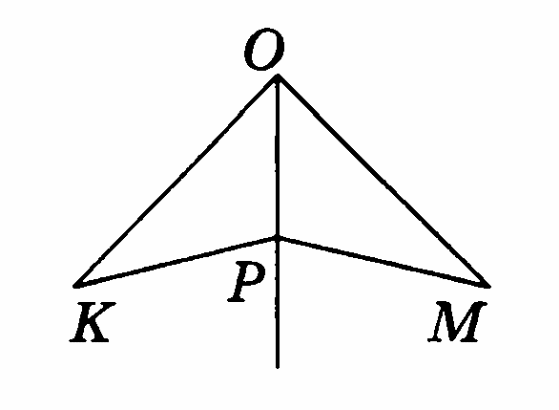
-
Даны два пересекающихся отрезка. Докажите, что ∆ОРМ = ∆ОКТ, если известно, что МО = ОТ и М =Т.
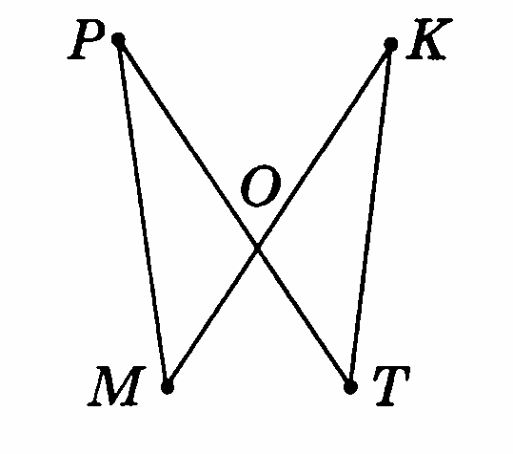
Вариант 2
-
Даны два пересекающихся отрезка. Докажите, что ∆АВК = ∆АСЕ, если точка А является серединой отрезка ВС и серединой отрезка ЕК.
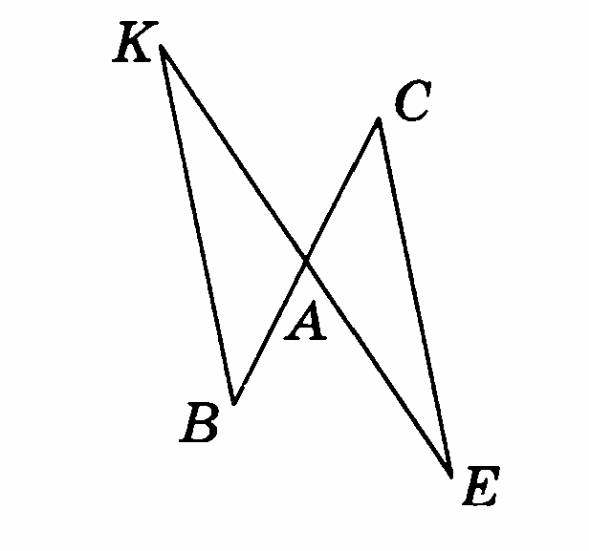
-
Равные углы ВАС и АСD отложены по разные стороны от прямой АС. Докажите, что ВС = АD, если ВСА = DАС.
Вариант 3
-
Луч ОР является биссектрисой угла КОМ. Докажите, что ∆КОР =∆МОР, еслиОРК = ОРМ.
-
Даны два пересекающихся отрезка. Докажите, что ∆ОРМ = ∆ОКТ, если известно, что РО = ОК и ОМ = ОТ.
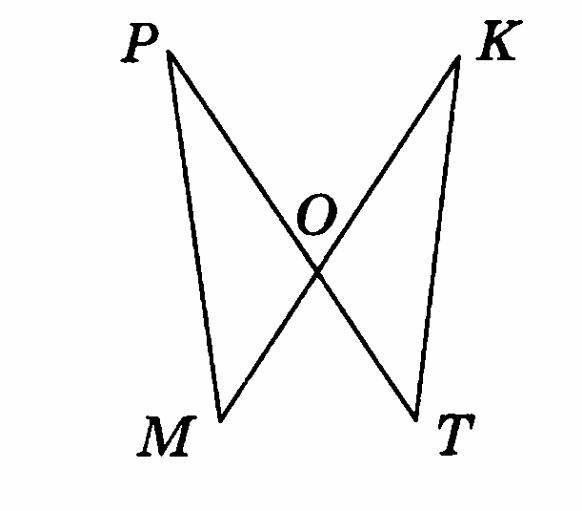
Вариант 4
-
Даны два пересекающихся отрезка. Докажите, что ∆МКВ = ∆МЕС, если точка М является серединой отрезка ВС и серединой отрезка ЕК.
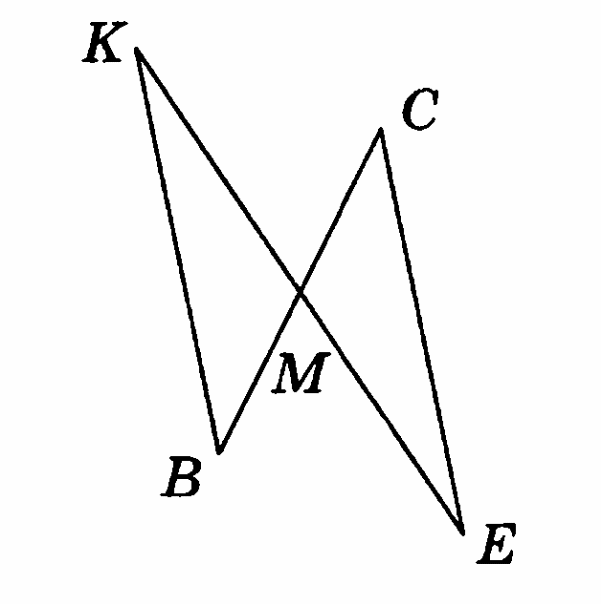
-
Равные углы ВАС и АСD отложены по разные стороны от прямой АС. Докажите, что АВ = СD, если АСВ =САD.
Вариант 5
-
На рисунке АD=DC, ADB = CDB. Докажите, что ABD = CBD.
-
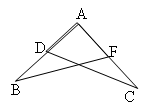
На рисунке АВ=АС, В = С. Докажите, что ВF = CD.
Вариант 6
-
В треугольниках АВС и ВАD САВ =DВА, СВА =DАВ, АD=2см. Найдите ВС.
-
Отрезки АМ и ВN – расстояния от точек А и В до прямой МN. Известно, что АМ=ВN. Докажите, что АNМ = ВМN.
Вариант 7
-
На рисунке 1 = 2, 3 = 4. Докажите, что В = D.
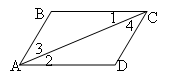
-
На рисунке AF=CF, AFD = CFD. Докажите, что АВ=СВ.
Вариант 8
-
На сторонах угла О отложены равные отрезки ОА и ОВ. Отрезок ОС – биссектриса угла О. Докажите равенство треугольников ОАС и ОВС.
-
Отрезок СD проходит через середину О отрезка АВ так, что САО = DВО. Найдите АС, если ВД=8см.
Вариант 9
-
В треугольниках АВС и АВD САВ = DАВ, СВА = DВА, ВС=8см. Найдите ВD.
-
Две прямые пересекаются в точке О. На одной прямой от точки О отложены равные отрезки ОА и ОВ, а на второй прямой - равные отрезки ОС и ОD. Докажите равенство треугольников ОАС и ОВD.
Вариант 10
-
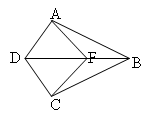
На рисунке АО = СО, ВО = DО, АВ = 5 см. Найдите СD.
-
На рисунке СО = DО, 1 =2. Доказать, что А = В.
Обучающая работа № 7: «Равнобедренный треугольник 1»
Вариант 1
-
Найдите периметр равнобедренного треугольника АВС с основанием АВ, если АВ = 7м, ВС = 8м.
-
Периметр равнобедренного треугольника равен 45м. Найдите боковые стороны, если основание равно 8м.
-
Треугольник АВС – равнобедренный с основанием АС. Докажите, что 3 = 4.
Вариант 2
-
Найдите периметр равнобедренного треугольника АВС с основанием АВ, если АВ = 8м, АС = 7м.
-
Периметр равнобедренного треугольника равен 45м. Найдите основание, если боковая сторона равна 18м.
-
Треугольник АВС – равнобедренный с основанием АС. Докажите, что 3 = 4.
Вариант 3
-
Составьте выражение для вычисления периметра равнобедренного треугольника, если его основание равно а и в 2 раза меньше боковой стороны.
-
Периметр равнобедренного треугольника равен 45м. Найдите все стороны, если боковая сторона на 3см больше основания.
-
Докажите равенство двух равнобедренных треугольников с общей боковой стороной, если равны их углы, противолежащие основаниям.
Вариант 4
-
Составьте выражение для вычисления периметра равнобедренного треугольника, если его боковая сторона равно b и на 3 меньше основания.
-
Периметр равнобедренного треугольника равен 45м. Найдите все стороны, если основание в 4 раза меньше боковой стороны.
-
По разные стороны от прямой АВ взяты точки К и N, такие, что АК = ВК, АN = ВN и ВАК = ВАN. Докажите, что треугольники ВАК и ВАN равны.
Вариант 5
-
Найдите периметр равнобедренного треугольника боковая сторона равна 14 см. а основание 16 см.
-
Периметр равнобедренного треугольника равен 90 см. Найдите основание, если боковая сторона равна 25 см.
-
Дано: АВ = ВС, ВАD = 105°. Найдите МСN.
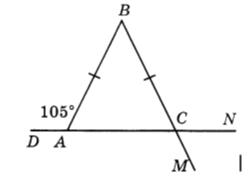
Вариант 6
-
Составьте выражение для вычисления периметра равнобедренного треугольника. Если его основание равно а, и боковая сторона в 3 раза больше основания.
-
Периметр равнобедренного треугольника равен 90 см. Найдите все стороны, если боковая сторона равна 15 см меньше основания.
-
Треугольник SPK - равнобедренный, SK – его основание. Чему равен 2, если 1 = 48°
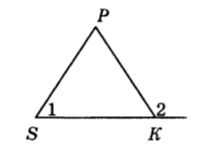
Вариант 7
-
Составьте выражение для вычисления периметра равнобедренного треугольника. Если его боковая сторона равна b, и основание на 4 больше боковой стороны.
-
Периметр равнобедренного треугольника равен 90 см. Найдите все стороны, если боковая сторона на 15 см больше основания.
-
Треугольник РОR – равнобедренный с основанием PR. Чему равен 1, если 2 = 42°.
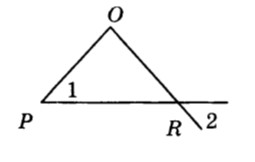
Вариант 8
-
Докажите, что медиана, проведенная к основанию, делит его на два равных треугольника.
-
Периметр равнобедренного треугольника равен 41 см, причем боковая сторона на 3,5 см меньше основания. Найти основание треугольника.
-
Докажите равенство двух равнобедренных треугольников с общим основанием, если у них равны углы при основаниях.
Вариант 9
-
Докажите, что высота, проведенная к основанию, делит его на два равных треугольника.
-
Периметр равнобедренного треугольника равен 45 см. Найдите его основание, если оно на 3 см больше боковой стороны.
-
По разные стороны от прямой МN взяты точки А и В так, что АМ=АN=МВ=ВN и АМN =ВМN Докажите, что ∆ АМN = ∆ ВМN.
Вариант 10
-
Докажите, что биссектриса, проведенная к основанию, делит его на два равных треугольника.
-
Периметр равнобедренного треугольника равен 45 см. Найдите его основание, если оно на 3 см меньше боковой стороны.
-
Докажите равенство двух равнобедренных треугольников с общей боковой стороной, если у них равны углы при основаниях.
Обучающая работа № 8: «Треугольник»
Вариант 1
-
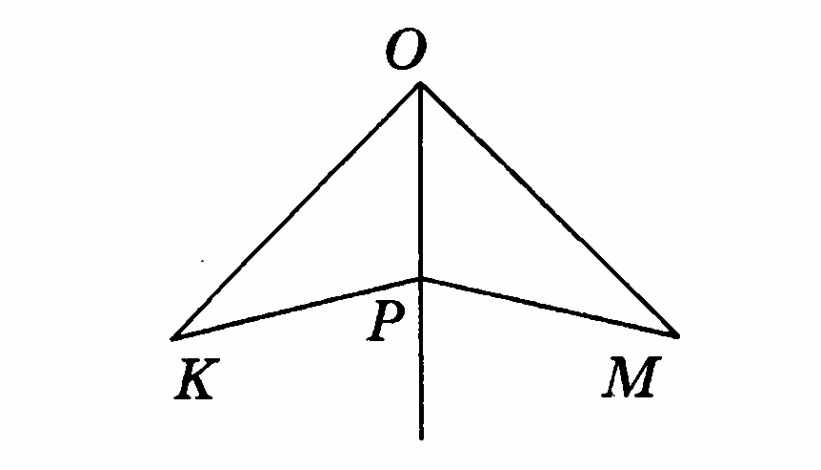
Найдите длину отрезка АМ и градусную меру угла АВК, если ВМ – медиана, а ВК – биссектриса треугольника АВС и АС = 16 м, АВС=84°.
Вариант 2
-
Найдите длину отрезка АМ и градусную меру угла АВК. Если ВМ – медиана, ВК – биссектриса треугольника АВС и АС = 22дм, СВА=70°
Вариант 3
-
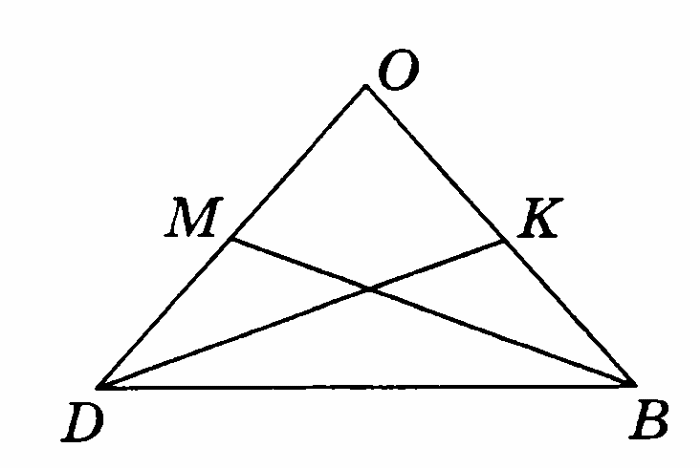 Треугольник DОВ – равнобедренный, ВD – его основание, DК и ВМ – медианы. Докажите, что:
Треугольник DОВ – равнобедренный, ВD – его основание, DК и ВМ – медианы. Докажите, что:
-
ВDМ = DВК;
-
DМ = ВК;
-
∆ ВDМ =∆ DВК.
Вариант 4
-
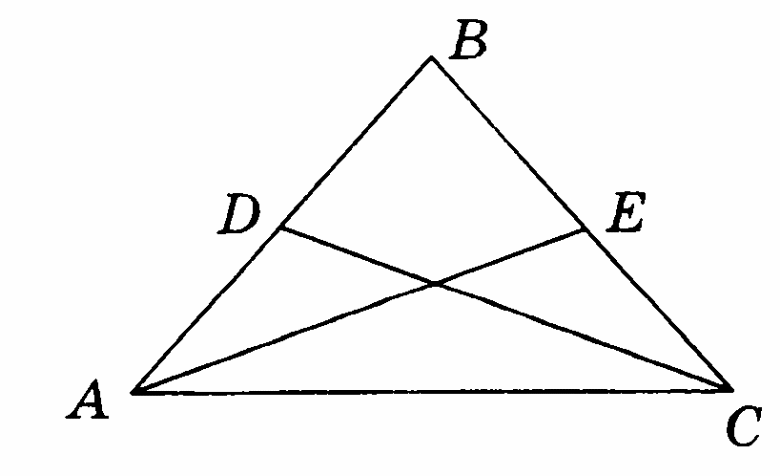 Треугольник АВС – равнобедренный, АС – его основание, СD и АЕ – биссектрисы. Докажите, что:
Треугольник АВС – равнобедренный, АС – его основание, СD и АЕ – биссектрисы. Докажите, что:
-
ВАС = ВСА;
-
ЕАС = DСА;
-
∆АСЕ =∆САД.
Вариант 5
-
Периметр равнобедренного треугольника равен 96 см, боковая сторона 30см. Чему равно основание этого треугольника?
Вариант 6
-
В треугольнике АВС высота ВК делит сторону АС пополам. Градусная мера угла А равна 75°. Чему равна величина угла С?
Вариант 7
-
Периметр равнобедренного треугольника равен 116 см. Основание больше боковой стороны на 14 см. Найдите боковую сторону.
Вариант 8
-
Периметр равнобедренного треугольника равен 68 см. Основание меньше боковой стороны на 10 см. Найдите боковую сторону.
Вариант 9
-
В равнобедренном треугольнике МКР с основанием КР проведена медиана МА. Периметр ∆МКР равен 76 см. а периметр ∆АРМ равен 34 см. Найдите длину медианы МА.
Вариант 10
-
В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Периметр ∆АВС равен 80 см. а периметр ∆АВМ равен 34 см. Найдите длину медианы АМ.
Обучающая работа № 9: «Равнобедренный треугольник 2»
Вариант 1
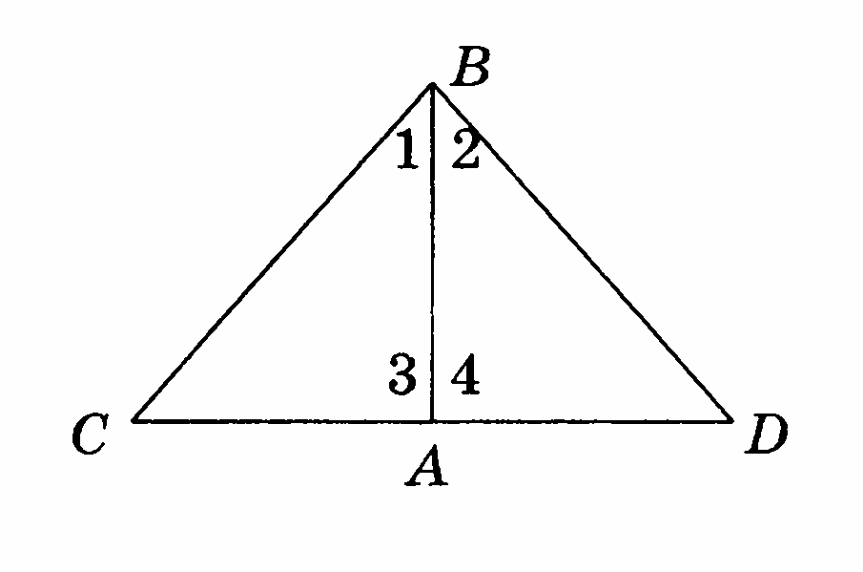
-
Треугольник СВD – равнобедренный с основанием DС, отрезок ВА – медиана. Найдите 1, 2, 3, 4, если СВD = 134°.
-
В равнобедренном треугольнике МОN c основанием МN на медиане ОР взята точка D. Докажите, что если на боковых сторонах отложены равные отрезки ОА и ОВ, то ∆ОАD = ∆ОВD.
Вариант 2
-
Треугольник СВД – равнобедренный с основанием ДС, отрезок ВА – медиана. Найдите 1, 2, 3, 4, если DВС = 121°.

-
В равнобедренном треугольнике МОN c основанием МN на медиане ОР взята точка D. Докажите, что если на основании отложены равные отрезки РА и РВ, то
∆РАD = ∆РВD.
Вариант 3
-
Найдите углы треугольника МКС, если МК – медиана равнобедренного треугольника СРМ с основанием СР, СМР = 104°, Р = 38°.
-
В равнобедренном треугольнике АВК основанием является сторона АВ. Точка О лежит на медиане КС. Докажите, что ∆ОАК = ∆ОВК.
Вариант 4
-
Найдите углы треугольника МКС, если КС – медиана равнобедренного треугольника ОКМ с основанием ОМ, ОКМ = 112°О = 34°.
-
В равнобедренном треугольнике АВК основанием является сторона АВ. Точка О лежит на медиане КС. Докажите, что ∆ОАС = ∆ОВС.
Вариант 5
-
Дано: АВ = ВС, АD =СD, МВА = 140°, ВАК = 110°. Найдите углы треугольника ВСD.
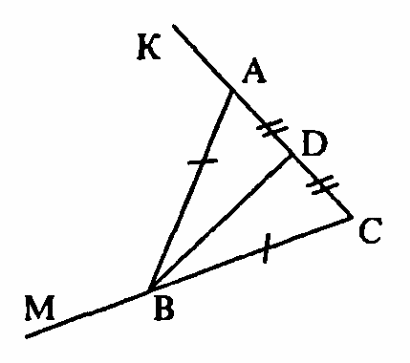
-
На основании АС равнобедренного треугольника АВС отметили точки М и К такие, что АМ = СК, точка М лежит между точками А и К. Докажите, что АВМ = СВК.
Вариант 6
-
Дано: Равнобедренный ∆DВС с основанием DС. D = 40°, ВА – медиана. Найдите СВА.
-
∆ МNK – равнобедренный, точки А и В – середины боковых сторон. Соедините их с точкой D, взятой на медиане NO и докажите, что ∆ АDN = ∆BDN.
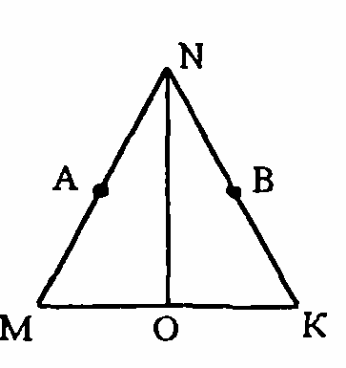
Вариант 7
-
В треугольнике АВС проведена медиана АМ, причём ВМ = АВ. ВМС = 108°. Найти
ВАМ.
-
Треугольник АВС – равнобедренный с основанием АВ. Найдите длину его высоты СМ, если периметр треугольника АВС равен 18 см, а периметр треугольника АСМ равен 12 см.
Вариант 8
-
Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
-
На боковых сторонах АВ и ВС равнобедренного треугольника АВС отметили соответственно точки Д и Е такие, что АСД = САЕ. Докажите, что АД =СЕ.
Вариант 9
-
Докажите, что в равнобедренном треугольнике биссектрисы углов при основании равны.
-
В равнобедренном треугольнике МNK c основанием МК длина его медианы NP равна 8 см. Периметр треугольника МNK равен 32 см. Найти периметр треугольника MNP.
Вариант 10
-
Найдите углы треугольника DКС, если КD - биссектриса равнобедренного треугольника МКС с основанием МС, МКС = 110°
-
На основании равнобедренного треугольника АВС отметили точки М и К такие, что АВМ = СВК, точка М лежит между точками А и К. Докажите, что АМ = СК.
Обучающая работа № 10: «Третий признак равенства треугольников»
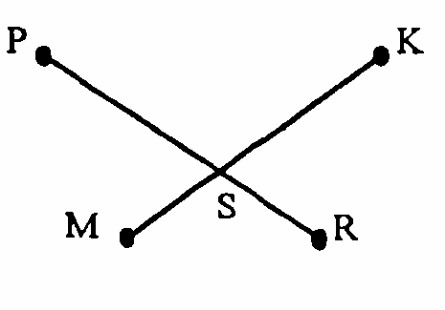
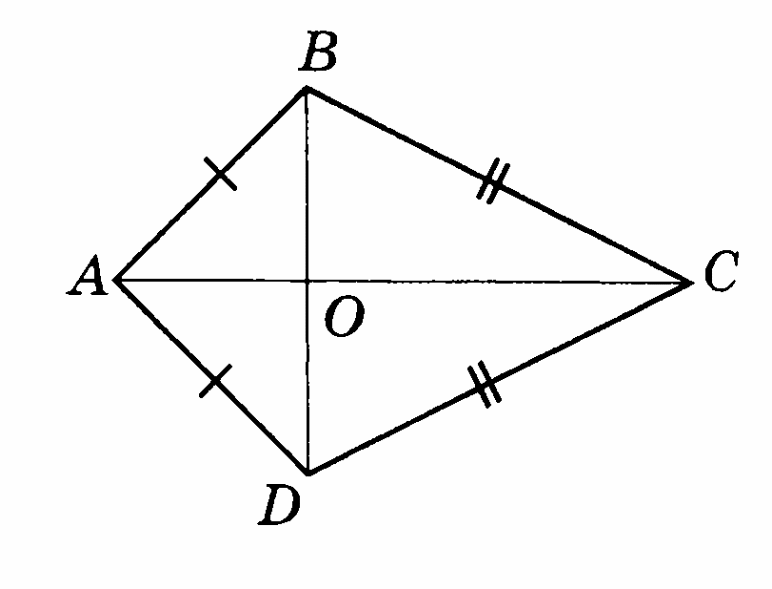
Вариант 1
-
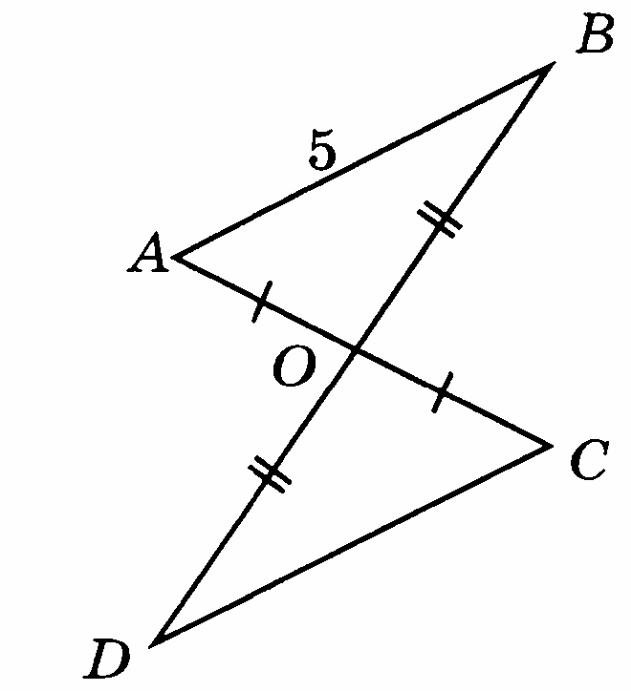
Точки В и D, лежащие по разные стороны от прямой МК, соединены с концами отрезка МК. Докажите, что ∆МВК = ∆КDМ, если МВ = КD и ВК = DМ.
-
Докажите равенство равнобедренных треугольников ВСD и ВСЕ с общим основанием ВС, если ВD = ВЕ.
Вариант 2
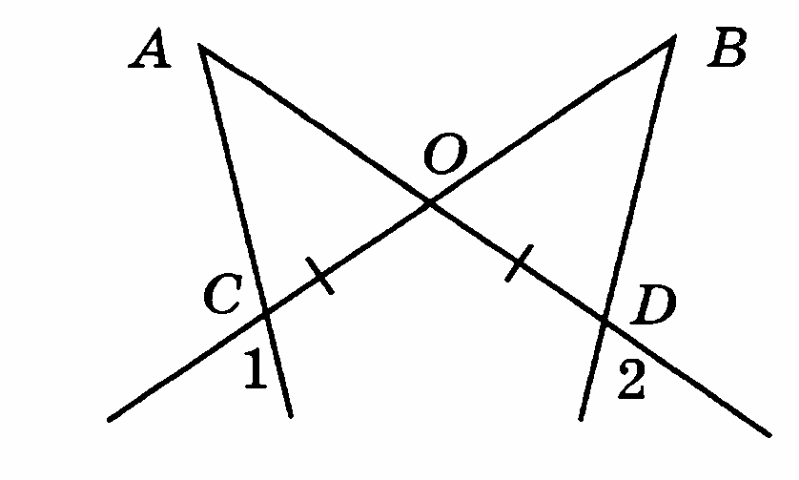
-
Точки А и В, лежащие по разные стороны от прямой МК, соединены с концами отрезка МК. Докажите, что ∆МАК = ∆МВК, если МА = ВК и АМК = ВКМ.
-
Докажите равенство равнобедренных треугольников АВС и АDС с общим основанием АС, если АВ = DС.
Вариант 3
-
На рисунке изображены равнобедренные треугольники, имеющие общую боковую сторону. Докажите, что ∆АВС =∆АВD, если равны их основания АС и АD.
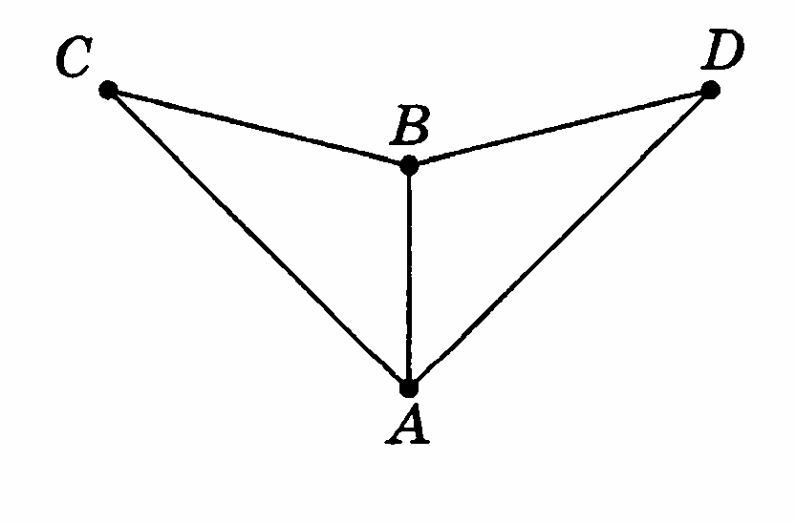
-
Треугольники АСD и АВD – равнобедренные с общим основанием АD. Докажите, что ∆АВС = ∆DВС, если точки В и С лежат по одну сторону от прямой АD.
Вариант 4
-
На рисунке изображены равнобедренные треугольники, имеющие общую боковую сторону. Докажите, что ∆ОМК =∆РМК, если равны их основания ОМ и МР.
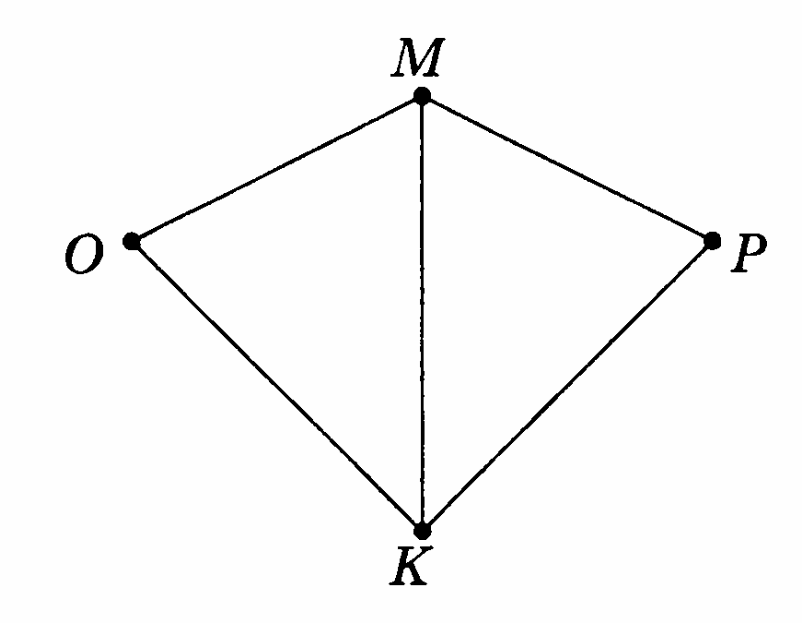
-
Треугольники АСD и АВD– равнобедренные с общим основанием АD. Докажите, что ∆АВС = ∆ DВС, если точки В и С лежат по разные стороны от прямой АD.
Вариант 5
-
На рисунке точка О – центр окружности, АО = АВ, ОС = СD. Докажите, что ∆АОВ = ∆СОD.
-
Отрезки МК и РК равны. Дополните рисунок и докажите равенство треугольников КРМ и РКR, если известно, что МР = RК.
Вариант 6
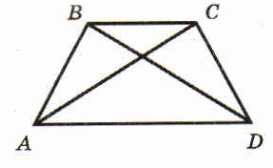
-
В равнобедренных треугольниках АОВ и СОВ равны основания АВ и ВС и АО=СО Докажите, что ∆АОВ = ∆СОВ.
-
На рисунке АВ = АД, СВ = СD. Докажите, что О – середина ВD.
Вариант 7
-
Дано: АВ = СD, АС = DВ. Докажите, что ВАD = СDА.
-
На рисунке АВ = СD, ВD = АС. Докажите, что АЕ = ЕD.
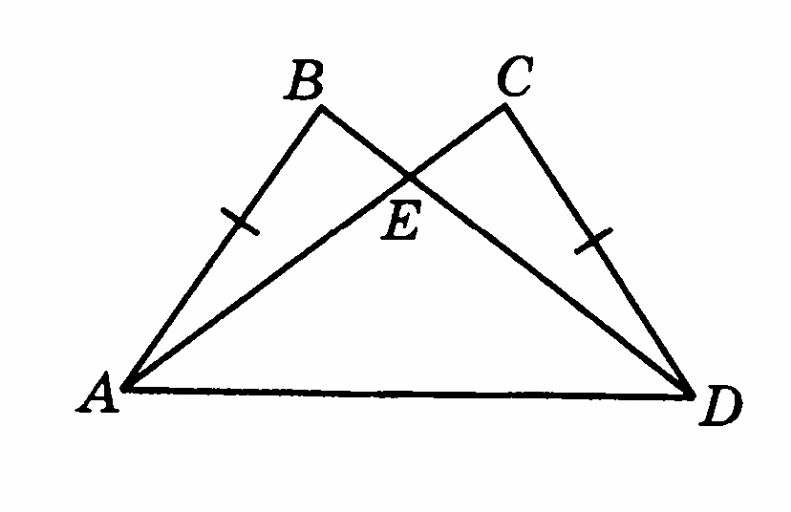
Вариант 8
-
На рисунке АВ = СD, АС = ВD. Докажите, что АСВ = DВС и АВD =DСА.
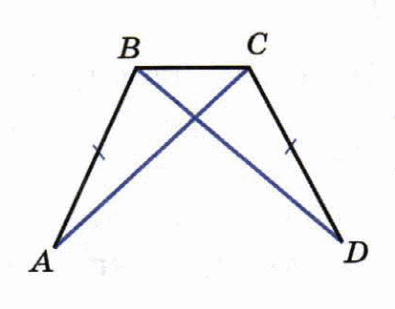
-
На рисунке АF = CF, AD = CD. Докажите, что АВ = СВ.
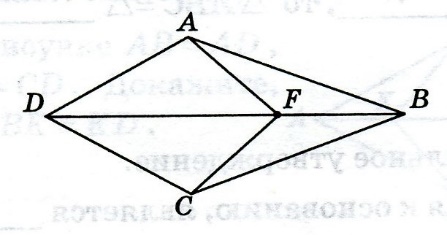
Вариант 9
-
На рисунке АВ = СD, АС = ВD. Докажите, что ВАС = СDВ и АСВ =DВС.
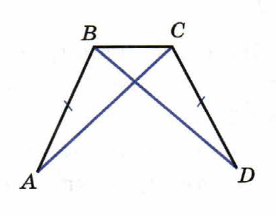
-
На рисунке АВ = CВ, AF = CF. Докажите, что АD = СD.
Вариант 10
-
В равнобедренных треугольниках МОВ и СОВ равны основания МВ и ВС и МО=СО Докажите, что ∆ МОВ = ∆ СОВ.
-
На рисунке АВ = АD, СВ = СD. Докажите, что ВО=ОD.
Параллельные прямые
Обучающая работа № 11: «Признаки параллельности прямых»
Вариант 1
-
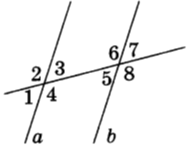
Объясните почему прямые а и в параллельны, если:
а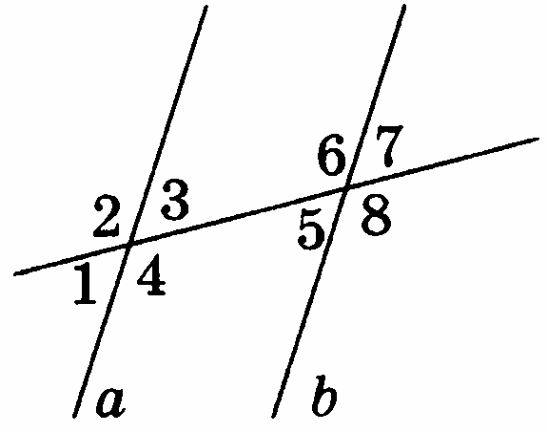 ) 3 = 5;
) 3 = 5;
б) 1 = 5
в) 3 + 6 = 180°.
-
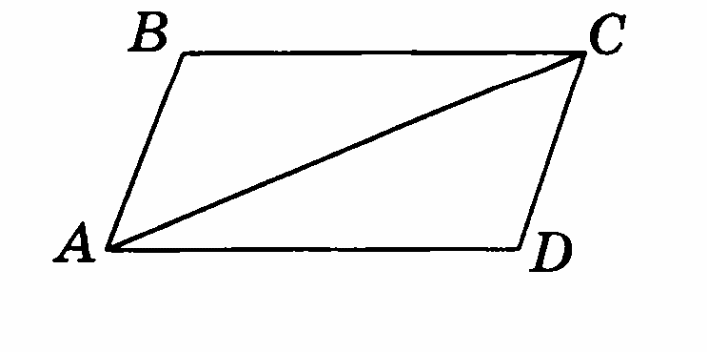
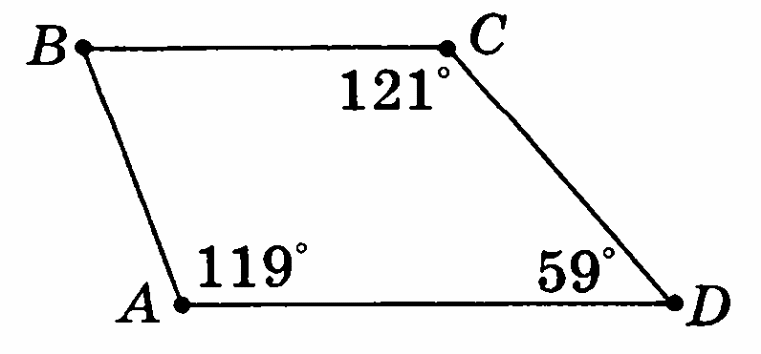
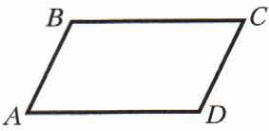
Определите, какие стороны параллельны у четырёхугольника АВСD.
Вариант 2
-
Объясните почему прямые а и в параллельны, если:
а ) 4= 6;
) 4= 6;
б) 3 = 7
в) 4 + 5= 180°.
2 Определите, какие стороны параллельны у четырёхугольника АВСD.
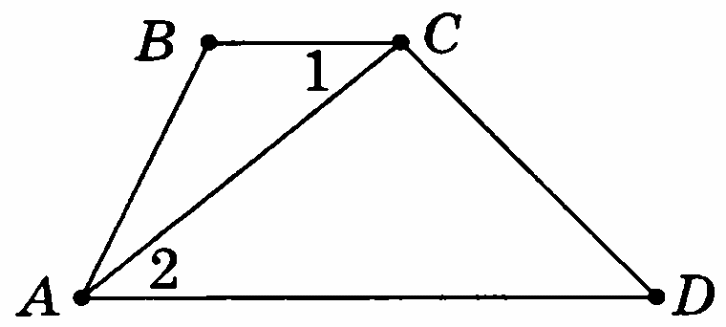
Вариант 3
-
Объясните почему прямые а и в параллельны, если:
а ) 3= 5;
) 3= 5;
б) 2 = 8
в) 1 + 6= 180°
-
Определите, какие стороны параллельны у четырёхугольника АВСD.
Вариант 4
-
Объясните почему прямые а и в параллельны, если:
а ) 4= 6;
) 4= 6;
б) 1 = 7
в) 2 + 5 = 180°.
-
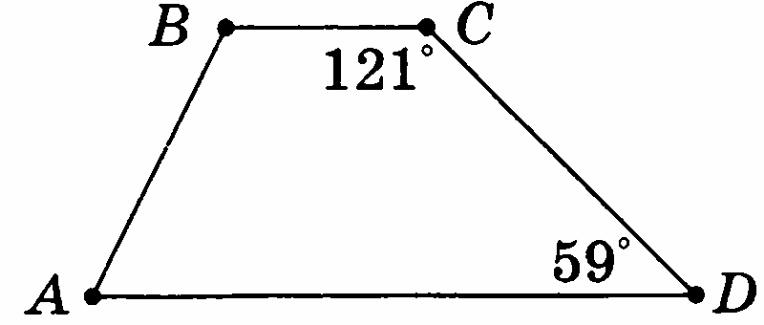
Определите, какие стороны параллельны у четырёхугольника АВСD.
Вариант 5
-
Укажите параллельные прямые, если 1=52°, 2 =128°, 3=128°.
-
Докажите, что АВ II ДК, если АВ=ВС, СD=DК.
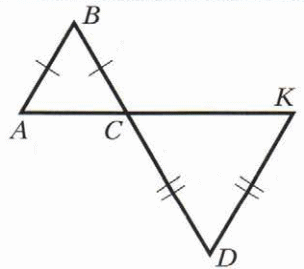
Вариант 6
-
На каких из рисунков а–г прямые а и b параллельны?
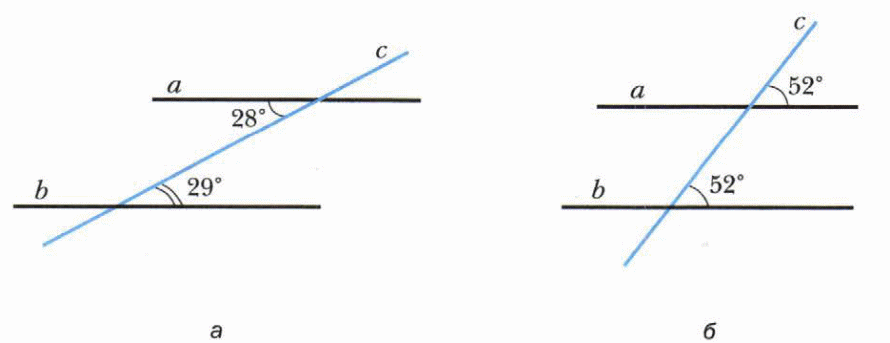
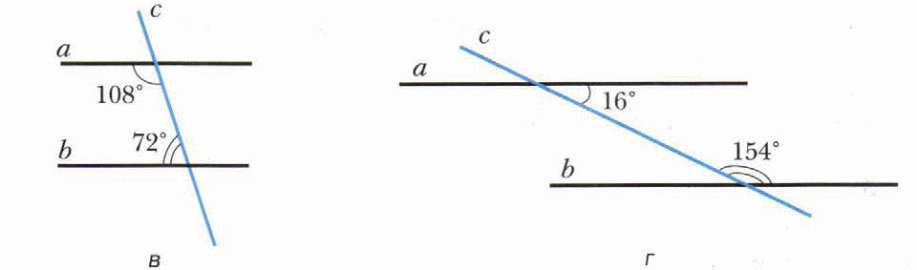
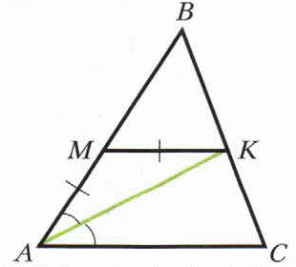
-
На рисунке АК – биссектриса угла ВАС, АМ = МК. Докажите, что МК II АС.
Вариант 7
-
. Параллельны ли прямые а и b, если
-
3=6;
-
2=6
-
4=125°; 6=55°
-
2=35°; 5=146°
-
1=98°; 6=82°
-
1=143°; 7=37°
-
На рисунке АСВ = АСD, АД = СD. Докажите, что ВС II АD.
Вариант 8
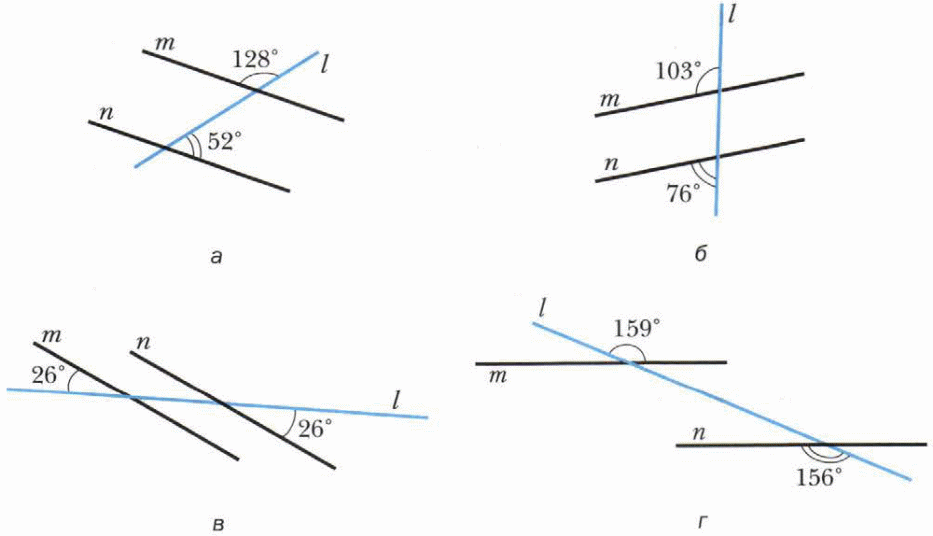
-
. На каких из рисунков а–г прямые m и n параллельны?
-
Отрезки АВ и СД пересекаются в точке О и делятся этой точкой пополам. Докажите, что АС II ВД.
Вариант 9
-
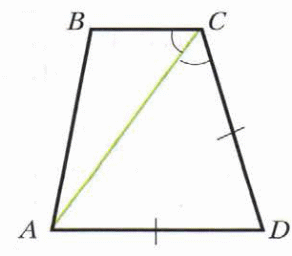
На рисунке укажите пары параллельных прямых.
-
В треугольнике АВС АВ = ВС, А = 60, ВСD – смежный с АСВ, СМ – биссектриса угла ВСD. Докажите, что АВ II СМ.
Вариант 10
-
. При пересечении двух прямых секущей образовались углы 1, 2 и 3. Известно, что углы 1 и 2 – вертикальные, а углы 2 и 3 – накрест лежащие. Как называются углы 1 и 3?
-
На рисунке АВ = СD, ВС = АД. Докажите, что АВ II СD.
Обучающая работа № 12: «Свойства параллельных прямых»
Вариант 1
-
. Определите 1 и 2, если прямые с и b параллельны и известно, что 3 = 103°.
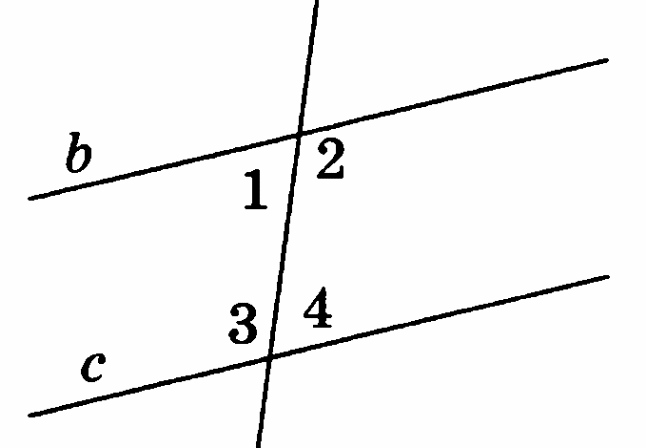
-
Прямые а и в параллельны. Найдите 5 и 6 если 1 = 43°.
Вариант 2
-
Определите 1 и 2, если прямые с и b параллельны и известно, что 3 = 113°.

-
Прямые а и в параллельны. Найдите 5 и 6 если 2 = 121° .

Вариант 3
-
Определите 1 и 2, если прямые с и b параллельны и известно, что 4 = 36°.

-
Прямые а и в параллельны. Найдите 7 и 8, если 4 = 133°.

Вариант 4
-
Определите 1 и 2, если прямые с и b параллельны и известно, что 4 = 46°.

-
Прямые а и в параллельны. Найдите 7 и 8 если 3 = 51°.

Вариант 5
-
На рисунке найдите угол 1.
-
На рисунке ВС = АD, ВС II АD. Докажите, что АВ II СD.
Вариант 6
-
На рисунке найдите угол 2.
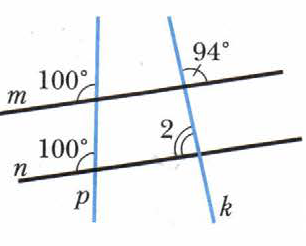
-
Через вершину В треугольника АВС провел прямую МК, параллельную прямой АС, МВА = 42°, СВК = 56°. Найдите углы треугольника АВС.
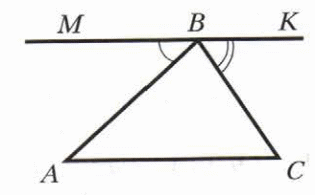
Вариант 7
-
Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.
-
На рисунке МАВ = 50°, АВК = 130°, АСВ = 40°, СЕ – биссектриса угла АСD. Найдите углы треугольника АСЕ.
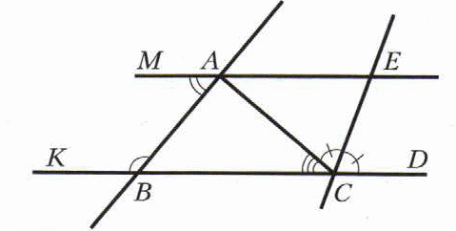
Вариант 8
-
Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы
-
На рисунке ВС II МК, ВК =КЕ, СК =КD. Доказать, что АD II МК.
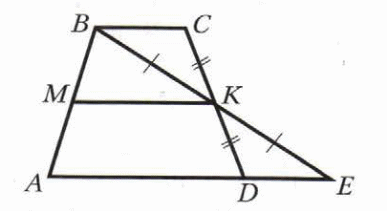
Вариант 9
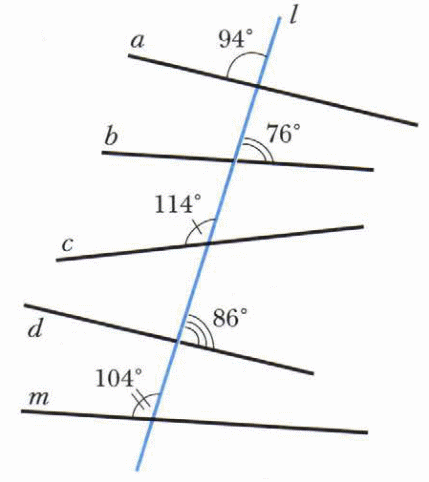
-
Найти все углы, образованные при пересечении двух параллельных прямых секущей, если один из углов равен 58°.
-
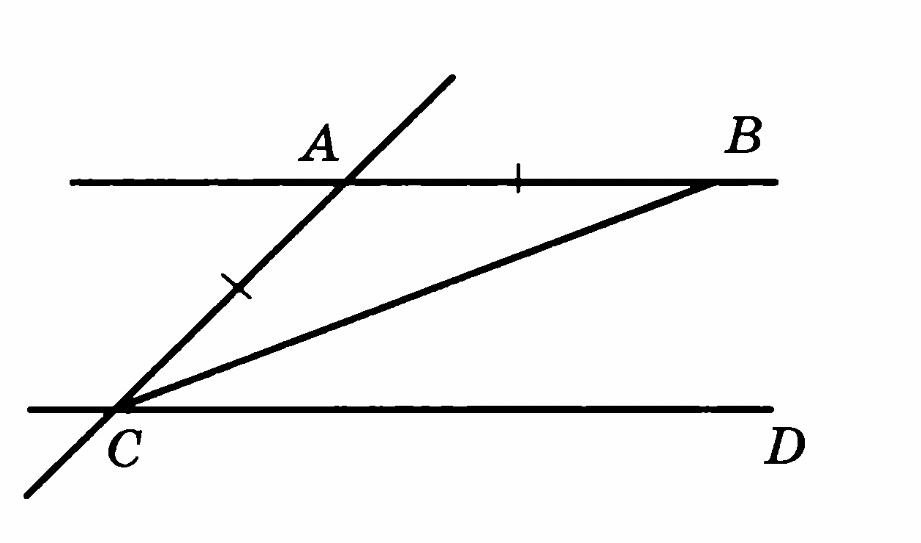
На рисунке ВС=АD и ВС II АD Докажите, что ∆ АВС = ∆ АDС.
Вариант 10
-
Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если отношение градусных мер двух из этих углов равно 2:7.
-
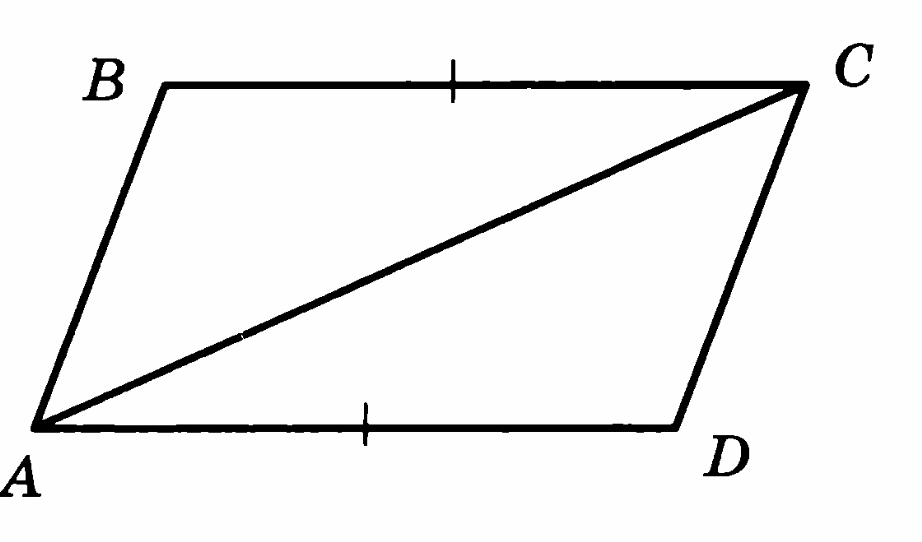
На рисунке АВ II CD и АС = АВ, ВСD = 20° Найти угол САВ.
Обучающая работа № 13: «Параллельные прямые»
Вариант 1
-
Найдите величину каждого из двух внутренних односторонних углов, если один из них больше другого в 4 раза.
-
Отрезки АС и ВD пересекаются в точке К, причём прямые ВС И АD параллельны. Докажите, что углы треугольника АDК соответственно равны углам треугольника СВК.
Вариант 2
-
Найдите величину каждого из двух внутренних накрест лежащих углов, если их сумма равна 72°.
-
Отрезки АВ и СD параллельны и равны. Докажите, что АВМ = СDМ, где М - точка пересечения отрезков АС и ВD.
Вариант 3
-
Найдите величину каждого из двух внутренних односторонних углов, если разность этих углов равна 72°.
-
Прямая, пересекающая боковые стороны равнобедренного треугольника, параллельна основанию. Докажите, что отсекаемый треугольник также является равнобедренным.
Вариант 4
-
Найдите величину каждого из двух внутренних накрест лежащих углов, если их сумма равна 142°.
-
Прямая, пересекающая основание равнобедренного треугольника, параллельна одной из боковых сторон. Докажите, что она отсекает равнобедренный треугольник.
Вариант 5
-
На рисунке а II в
Найдите 1 и 2.
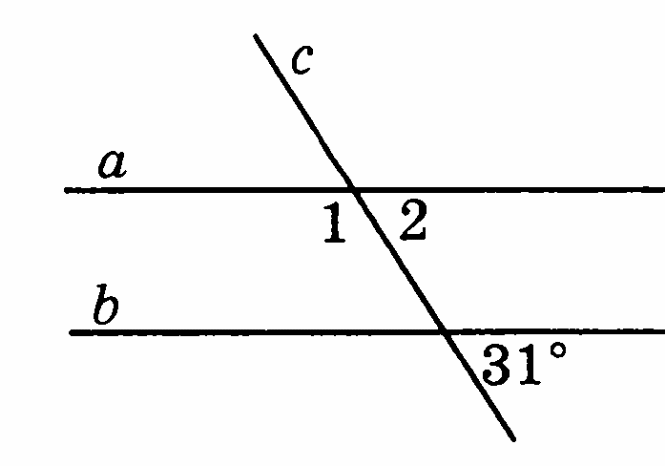
-
При пересечении двух данных прямых секущей образовались односторонне углы, один из которых равен 45°, а другой в 3 раза больше. Докажите, что данные прямые параллельны.
Вариант 6
-
На рисунке а II в
Найдите 1 и 2.
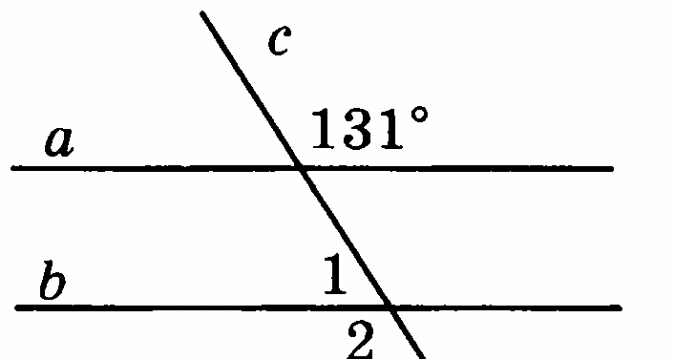
-
При пересечении двух данных прямых секущей образовались односторонне углы, один из которых равен 150°, а другой в 5 раза меньше. Докажите, что данные прямые параллельны.
Вариант 7
-
Найдите угол х
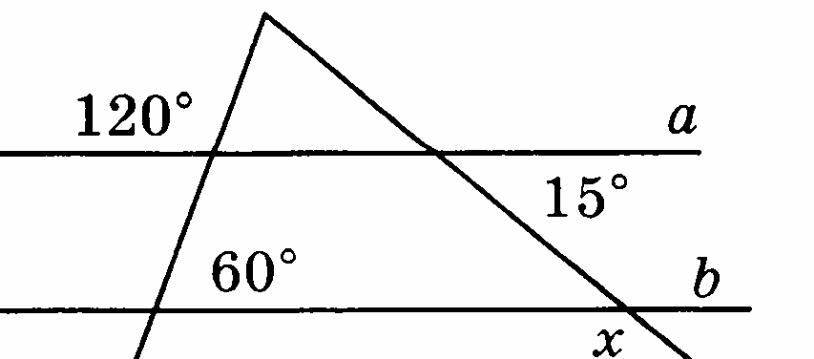
-
При пересечении двух данных прямых секущей образовались односторонне углы, разность которых равна 36°, а отношение – 3:2 . Докажите, что данные прямые параллельны.
Вариант 8
-
Найдите угол х .
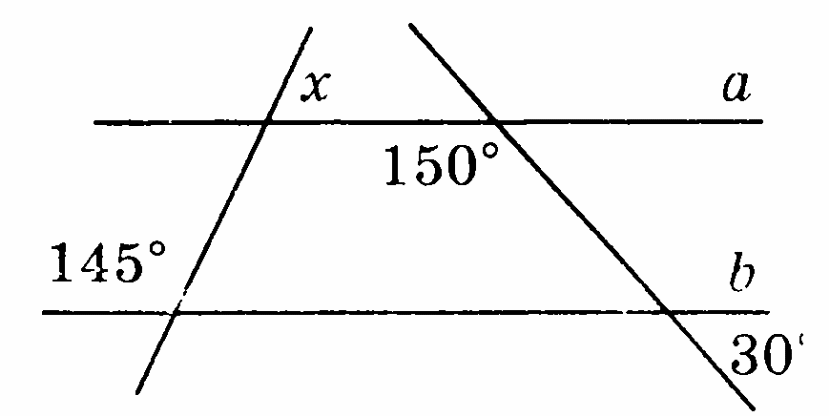
-
При пересечении двух данных прямых секущей образовались односторонне углы, разность которых равна 108°, а отношение – 4:1. Докажите, что данные прямые параллельны.
Вариант 9
-
Найдите угол х

-
Отрезки АВ и СD параллельны и равны, а отрезки АD и ВС пересекаются. Докажите, что ∆АВС =∆DСВ.
Вариант 10
-
Найдите угол х
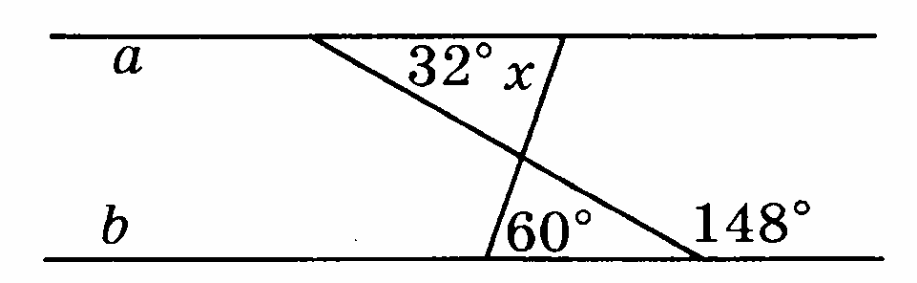
-
Отрезки АВ и СD параллельны и равны. Докажите, что ∆АОВ =∆DОС, где О – точка пересечения отрезков АD и ВС.
Соотношения между сторонами и углами треугольника
Обучающая работа № 14: «Сумма углов треугольника (1)»
Вариант 1
-
В треугольнике DВС проведена биссектриса DК. Определите углы треугольника DВС, если СDК = 37°, DКС = 105°.
-
В равнобедренном треугольнике АВС с основанием ВС биссектрисы ВМ и СN пересекаются в точке О. Найдите углы треугольников СВМ и ВОС, если А = 68°
Вариант 2
-
Найдите углы равнобедренного треугольника, если угол при основании больше угла между боковыми сторонами в 4 раза.
-
Прямая, параллельная стороне МК треугольника МNК, отсекает от него треугольник NОР, в котором N = 71°, NОР =34°. Определите углы треугольника МNК.
Вариант 3
-
В треугольнике DВС проведена биссектриса DК. Определите углы треугольника DВС, если ВDК = 35°, ВКD = 48°.
-
В равнобедренном треугольнике АВС с основанием ВС биссектрисы ВМ и СN пересекаются в точке О. Найдите углы треугольников СВМ и ВОС, если АВС = 56°.
Вариант 4
-
Найдите углы треугольника, если один из них в 2 раза больше другого и на 20° больше третьего.
-
В равнобедренном треугольнике один из углов равен 56°. Найдите остальные углы.
Вариант 5
-
Найдите углы равностороннего треугольника.
-
На рисунке В = 24°, АВ = ВС. Найдите А и С.
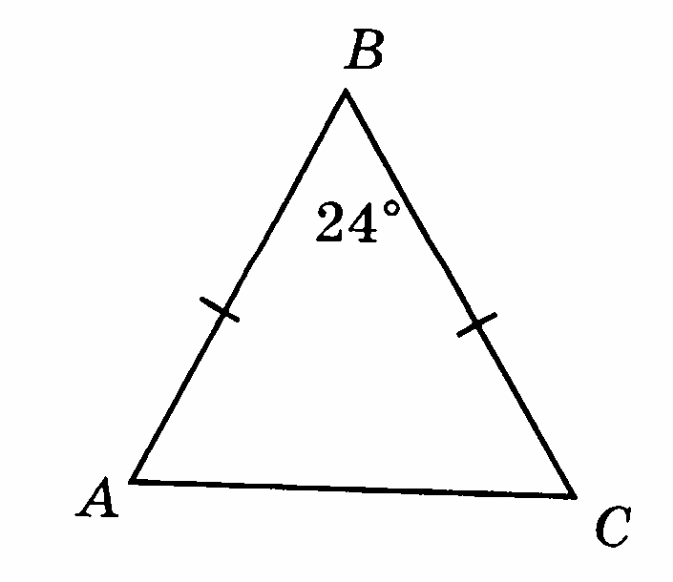
Вариант 6
-
В треугольнике АВС АВ =ВС, СК – биссектриса, А = 66°. Найдите АКС.
-
На рисунке В = 70°, С = 33°. Докажите, что ВС АВ.
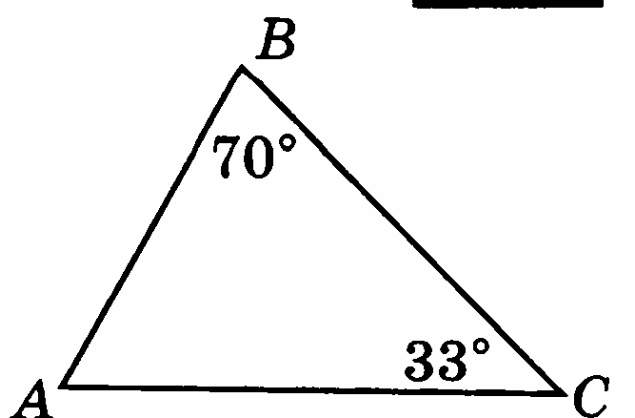
Вариант 7
-
Биссектрисы АК и СМ треугольника АВС пересекаются в точке О, ВАС =116°,
ВСА = 34°. Найдите АОС
-
На рисунке ВС II АD, А = 25°, В = 55°, Найдите угол СМD.
Вариант 8
-
В равнобедренном треугольнике АВС с углом при вершине В, равным 36°, провели биссектрису АД. Докажите, что треугольники АDВ и САD - равнобедренные.
-
На рисунке А = 42°, С = 53°. Докажите, что АС АВ.
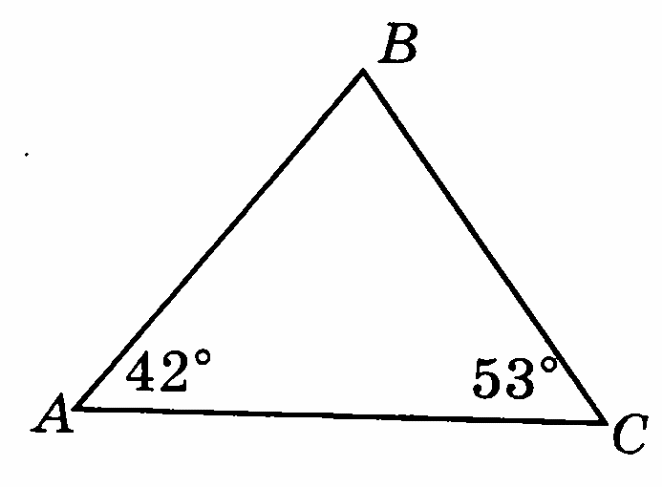
Вариант 9
-
Отрезок ВК - биссектриса равнобедренного треугольника АВС с основанием ВС, АКВ = 105°. Найдите углы треугольника АВС.
-
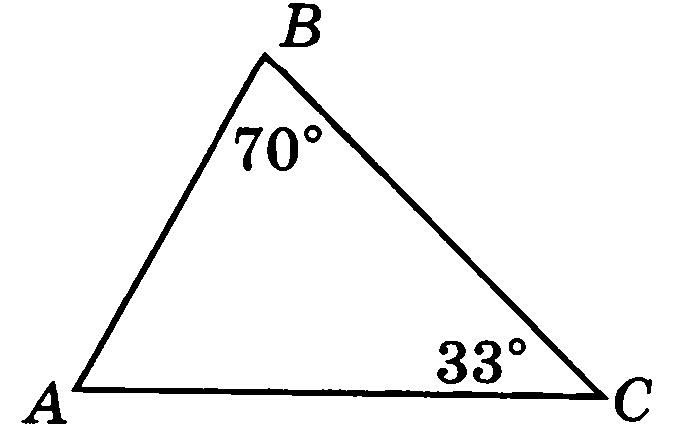
На рисунке В = 70°, С = 33°. Докажите, что ВС АВ.
Вариант 10
-
Найдите углы равнобедренного треугольника, если угол, противолежащий основанию, на 24° больше угла при основании.
-
На рисунке АВ = 4см, ВС = 6см, 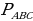 = 15см. Докажите, что А B
= 15см. Докажите, что А B
Обучающая работа № 15: «Сумма углов треугольника (2)»
Вариант 1
-
Найдите внешние углы треугольника, если известны два его внутренних угла 35° и 79°.
-
Найдите неизвестные углы треугольника, если один из них равен 31°, а один из внешних углов равен 132°.
-
Найдите углы равнобедренного треугольника, если внешний угол при вершине, противолежащий основанию, равен 54°.
Вариант 2
-
Найдите внешние углы треугольника, если известны два его внутренних угла 37° и 64°.
-
Найдите углы равнобедренного треугольника, если внешний угол при основании, равен 118°.
-
Найдите углы при основании МР равнобедренного треугольника МОР, если МК – его биссектриса и ОКМ = 93°.
Вариант 3
-
Найдите углы треугольника, если известны два его внешних угла 121° и 82°
-
Найдите неизвестные углы треугольника, если один из них равен 30°, а один из внешних углов равен 135°.
-
Найдите углы равнобедренного треугольника, если внешний угол при вершине, противолежащий основанию, равен 154°.
Вариант 4
-
Найдите углы треугольника, если известны два его внешних угла 135° и 153°
-
Найдите углы равнобедренного треугольника, если внешний угол при основании, равен 146°.
-
Найдите неизвестные углы треугольника АВС, если А = 84°, а угол В в 5 раз меньше внешнего угла при вершине С.
Вариант 5
-
Найти углы равнобедренного треугольника, если один из его внешних углов равен 54°
-
На рисунке АС II ВD, СВD = 43°, DВЕ = 37°. Найдите углы треугольника АВС.
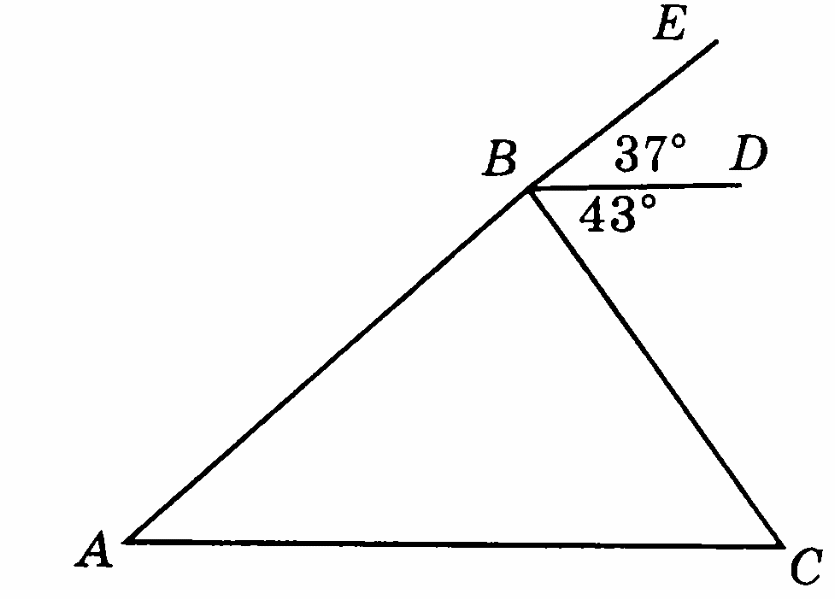
-
Внешний угол треугольника равен 134°, а внутренний угол, не смежный с ним, - 47°. Найдите неизвестные углы треугольника.
Вариант 6
-
Найти углы равнобедренного треугольника, если один из его внешних углов равен 112°.
-
На рисунке АВ = ВС, DВА = 120°. Докажите, что ∆АВС – равносторонний.
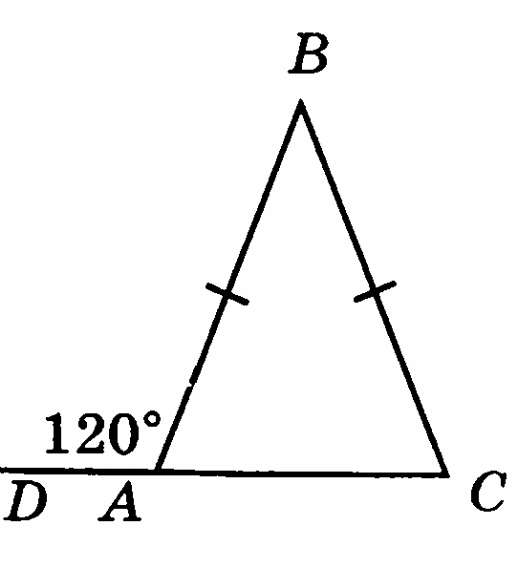
-
Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.
Вариант 7
-
Один из внешних углов треугольника равен 75°. Чему равны:
1) Угол треугольника при этой вершине;
2) Сума двух углов треугольника, не смежных с ним
-
На рисунке АД=ВС=СD, АDВ = 144°. Найти углы треугольника АВС.
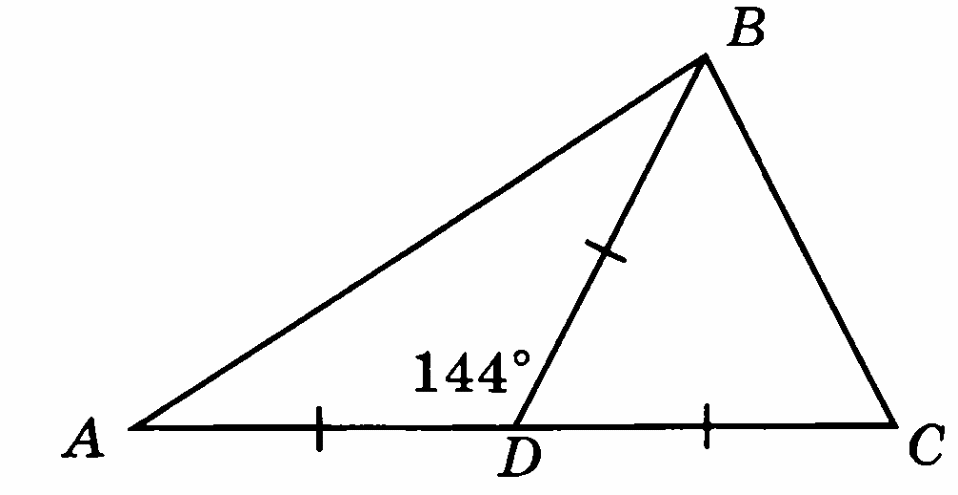
-
Докажите, что если биссектриса внешнего угла треугольника параллельна его стороне, то этот треугольник равнобедренный.
Вариант 8
-
Один из внешних углов треугольника равен 136°, один из углов треугольника, не смежный с ним, - 61°. Найдите второй угол треугольника, не смежный с данным внешним.
-
На рисунке АД = ВС = СD, DВС = 22°. Найти углы треугольника АВС.
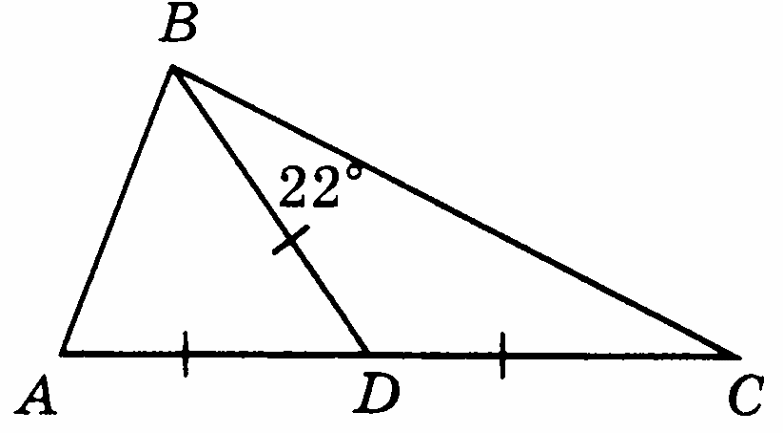
-
Два внешних угла треугольника равны 104° и 124°. Найдите углы треугольника.
Вариант 9
-
. Один из внешних углов треугольника равен 154°. Найдите углы треугольника, не смежные с ним, если один из этих углов на 28° больше другого.
-
На рисунке АВ II СD, ВСD = 58°, DСЕ = 62°. Найти углы треугольника АВС.
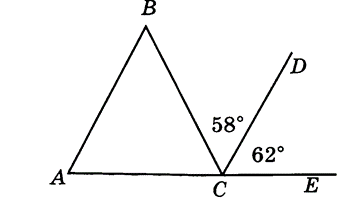
-
Сумма одной пары внешних углов треугольника равна 194°, а сумма другой пары внешних углов – 321°, Найдите углы треугольника.
Вариант 10
-
Определить вид треугольника, если один из его внешних углов равен углу треугольника, смежному с ним.
-
На рисунке АВ = ВС, DВС = 120°. Докажите, что ∆АВС – равносторонний.
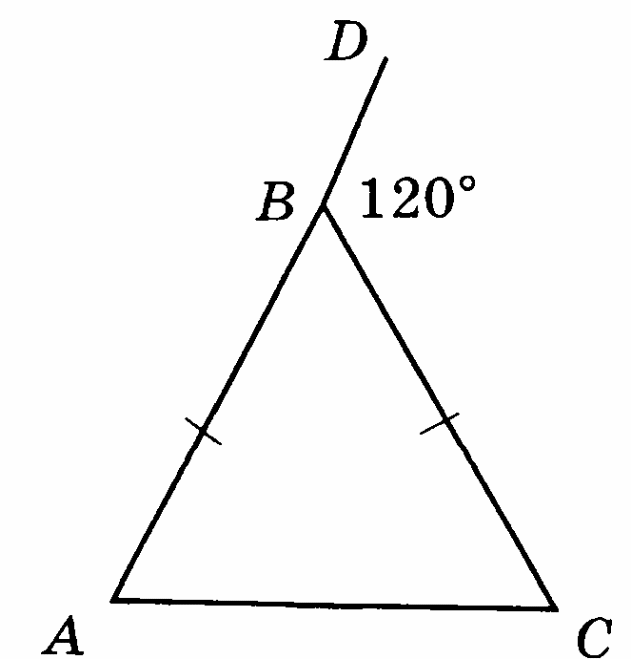
-
Внешние углы треугольника относятся как 10:9:5. Найдите углы треугольника.
Обучающая работа № 16: «Прямоугольный треугольник»
Вариант 1
-
Треугольник АВС – прямоугольный с прямым углом С, отрезок СD является его высотой. Найдите острые углы треугольника АВС, если АСD = 42°.
-
Точки А и В лежат по разные стороны от прямой МК, АМ и ВК –перпендикуляры к этой прямой. Докажите, ∆АМК = ∆ВКМ, если АК = ВМ.
Вариант 2
-
Треугольник АВС – прямоугольный с прямым углом С, отрезок СD является его высотой. Найдите острые углы треугольника АВС, если ВСD = 37°.
-
К прямой АВ проведены в разные полуплоскости перпендикуляры АМ и ВК. Отрезки МК и АВ пересекаются в точке О. Докажите, что ∆АОМ = ∆ВОК, если АМ = ВК.
Вариант 3
-
Треугольник АВС – прямоугольный с прямым углом С, отрезок СD является его высотой. Докажите, что у треугольников АВС и АСD углы соответственно равны
-
Точки А и В лежат по разные стороны от прямой, АМ и ВК –перпендикуляры к этой прямой. Докажите, ∆АМК = ∆ВКМ, если МАК = МВМ.
Вариант 4
-
Треугольник АВС – прямоугольный с прямым углом С, отрезок СD является его высотой. Докажите, что у треугольников АВС и ВСD углы соответственно равны.
-
К прямой АВ проведены в разные полуплоскости перпендикуляры АМ и ВК. Отрезки МК и АВ пересекаются в точке О. Докажите, что ∆АОМ = ∆ВОК, если известно, что О – середина отрезка МК.
Вариант 5
-
На рисунке СD = 9см. Найдите АВ.
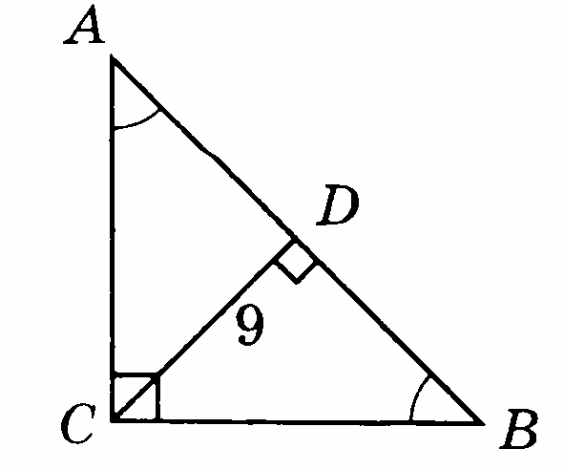
-
Биссектрисы прямого и острого углов прямоугольного треугольника при пересечении образуют углы, один из которых равен 132°. Найти острые углы треугольника.
Вариант 6
-
На рисунке АD = 12см. Найдите расстояние от точки С до прямой АВ.
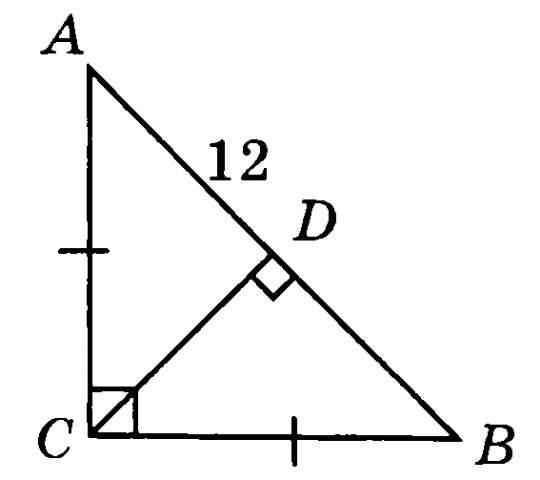
-
Биссектрисы прямого и острого углов прямоугольного треугольника при пересечении образуют углы, один из которых равен 54°. Найти острые углы треугольника.
Вариант 7
-
На рисунке СD = 7см. Найдите АВ и А
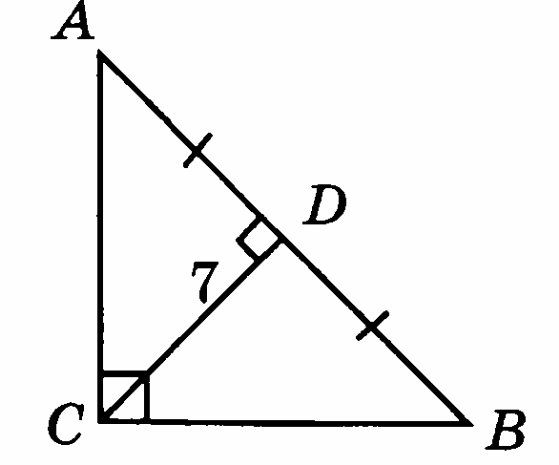
-
Острый угол прямоугольного треугольника равен 38°. Найдите угол между биссектрисой и высотой, проведенными из вершины прямого угла.
Вариант 8
-
На рисунке ВD = 5см. Найдите расстояние от точки С до прямой АВ и В.
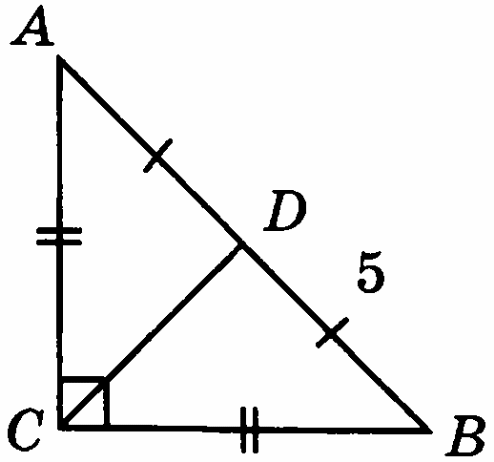
-
Угол между биссектрисой и высотой, проведёнными из вершины прямого угла прямоугольного треугольника, равен 12°. Найдите острые углы треугольника.
Вариант 9
-
На рисунке А = 30°, АВ = 22. Найдите расстояние от точки В до прямой АС.
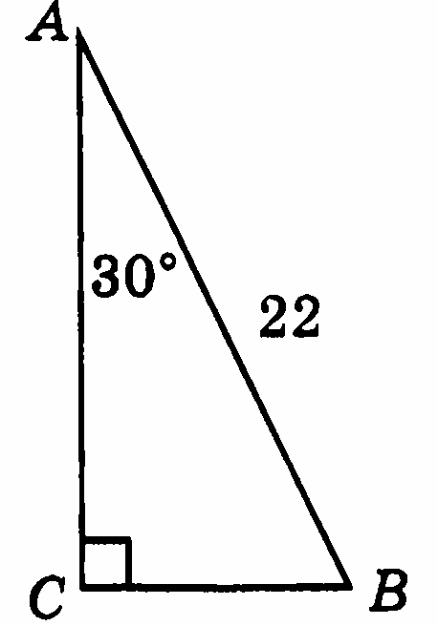
-
В прямоугольном треугольнике из вершины угла, равного 60°, проведена биссектриса, длина которой равна 18 см. Найдите длину катета, лежащего против данного угла.
Вариант 10
-
На рисунке АВ = 38см, ВС = 19см. Найдите ТВК.
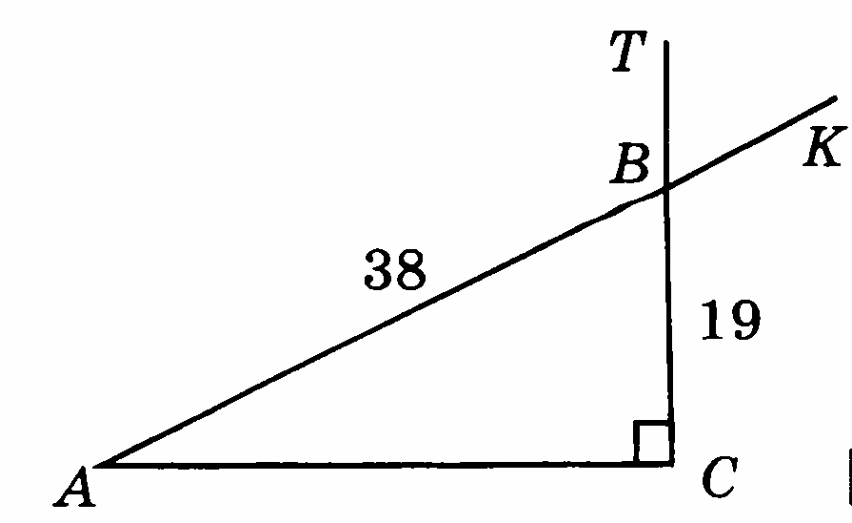
-
В прямоугольном треугольнике из вершины угла, равного 60°, проведена биссектриса. Расстояние от основания биссектрисы до вершины другого острого угла равно 14см. Найти расстояние от основания биссектрисы до вершины прямого угла.
Окружность
Обучающая работа № 17: «Окружность»
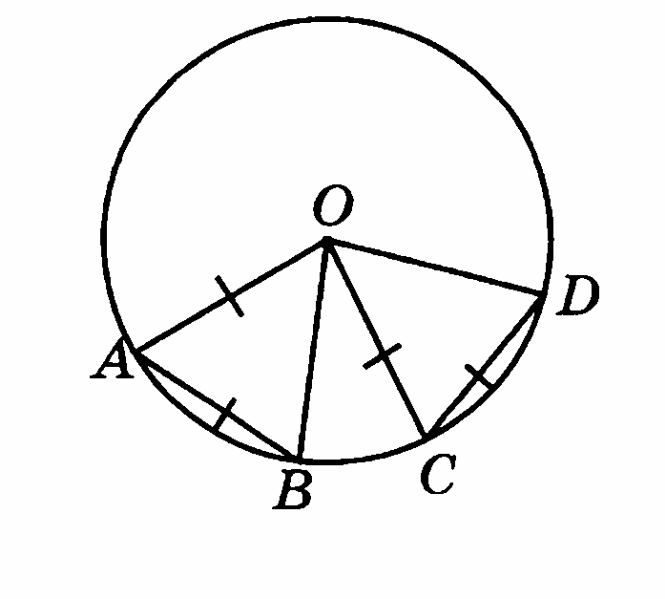
Вариант 1
-
В окружности с центром О проведена хорда КМ. Найдите неизвестные углы треугольника ОКМ, если ОМК = 47°.
-
Точка М – середина хорды ВС. Она соединена с центром О окружности. Найдите углы треугольника ВОМ, если ВОС = 148°.
-
В окружности с центром О проведены радиусы ОМ, ОК и ОN. Докажите, что ∆МОК =∆NОК, если известно, что хорды МК и NК равны.
Вариант 2
-
В окружности с центром О проведена хорда КМ. Найдите неизвестные углы треугольника ОКМ, если КОМ = 52°.
-
Точка М - середина хорды ВС. Она соединена с центром О окружности. Найдите углы треугольника ВОМ, если ВСО = 71°.
-
В окружности с центром О проведены радиусы ОМ, ОК и ОN. Докажите, что ∆МОК =∆NОК, если известно, что МОК = NОК.
Вариант 3
-
В окружности с центром О проведены диаметр АВ и хорда ВD. Определите углы треугольника ВОD, если АОD = 114°.
-
В окружности проведены диаметры МР и DF.Докажите, что хорды МD и РF равны.
-
Точка О – центр окружности. Докажите, что ∆АОВ = ∆DОС, если известно, что хорды АВ и СD равны.
Вариант 4
-
В окружности с центром О проведены диаметр АВ и хорда ВD. Определите АОD, если АВD = 44°.
-
В окружности проведены диаметры МР и DF.Докажите, что МFD = РDF
-
Через точки М и К, лежащие на окружности с центром О, проведены касательные МN и КN. Докажите, что ∆МОN = ∆КОN.
Вариант 5
-
Хорды АВ и СD окружности с центром О равны. Докажите, что АОВ = СОD.
-
Точка О – центр окружности, АВ и АС – касательные к окружности; А = 40°. Найти ВОС.
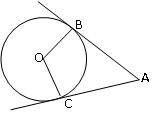
-
Найти расстояние между центрами двух окружностей, касающихся внешне, если радиусы равны 32 см и 5,3дм.
Вариант 6 СОД
-
На рисунке точка О – центр окружности, СОD = МОК Докажите, что хорды СD и МК равны.
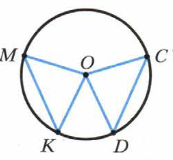
-
Точка О – центр окружности, АС и ВС – касательные к окружности АОВ =120°. Найти АСВ
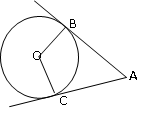
-
Найти расстояние между центрами двух окружностей, касающихся внешне, если радиусы равны 35см и 5,7дм
Вариант 7
-
Отрезки АВ и СD - диаметры окружности с центром О. Докажите, что ВАС =СDВ
-
Точка О – центр окружности. АВ и АС – касательные. ВОС = 100°. Найти А
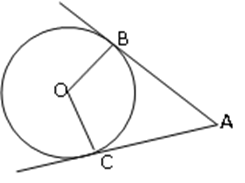
-
Расстояние между центрами двух окружностей, касающихся внутренне, равно 15 см. Найти радиусы этих окружностей, если один из них в 2 раза меньше второго.
Вариант 8
-
Отрезки МК и ЕF диаметры окружности с центром О, МК = 12см, МЕ = 10см. Найдите периметр треугольника FОК.
-
Дано: ВОС = 63°, О – центр окружности. Найдите АОС.
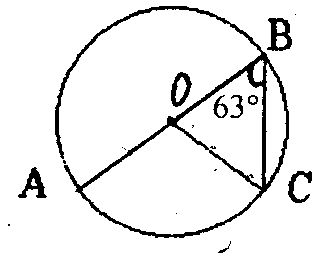
-
Расстояние между центрами двух окружностей, касающихся внутренне, равно 36 см. Найти радиусы этих окружностей, если один из них в 4 раза больше второго.
Вариант 9
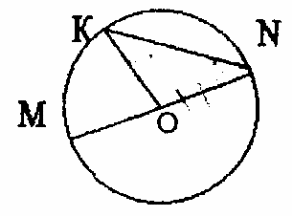
-
Отрезки АС и АВ – соответственно диаметр и хорда окружности с центром О. ВАС = 26°. Найти ВОС.
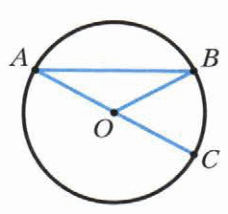
-
Дано: КОМ = 87°, О – центр окружности. Найти КNМ.
-
Точка касания вписанной в равнобедренный треугольник окружности разделяет боковую сторону этого треугольника на отрезки 5 см и 6 см, считая от основания. Найдите периметр этого треугольника.
Вариант 10
-
Отрезки МР и МК – соответственно диаметр и хорда окружности с центром О.
РОК = 84°. Найдите МРО.
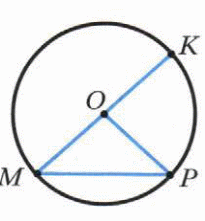
-
Отрезок СD – диаметр окружности с центом О. На окружности отметили точку Е так, что СОЕ =90. Докажите, что СЕ = DЕ.
-
Точка касания вписанной в равнобедренный треугольник окружности разделяет боковую сторону этого треугольника на отрезки 3 см и 4 см, считая от вершины, противоположной основанию. Найти периметр этого треугольника.
Построения
Обучающая работа № 18: «Построения»
Вариант 1
-
. Даны отрезки b и угол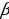 . Постройте равнобедренный треугольник с боковой стороной, равной b, и углом, противолежащим основанию, равным
. Постройте равнобедренный треугольник с боковой стороной, равной b, и углом, противолежащим основанию, равным 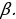
-
Постройте прямоугольный треугольник по катету и гипотенузе.
Вариант 2
-
Даны отрезки b и угол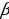 . Постройте равнобедренный треугольник с основанием, равным b, и углом, при основании, равным
. Постройте равнобедренный треугольник с основанием, равным b, и углом, при основании, равным  .
.
-
Начертите произвольный треугольник АВС. Постройте биссектрису угла АМ.
Вариант 3
-
Постройте прямоугольный треугольник по двум катетам.
-
Начертите треугольник МРК с тупым углом Р. Постройте высоту КА.
Вариант 4
-
Постройте прямоугольный треугольник по катету и прилежащему острому углу.
-
Дан отрезок АВ. Постройте окружность, для которой отрезок АВ является диаметром.
Вариант 5
-
Построить треугольник по трём его сторонам.
-
Построить треугольник по двум сторонам и медиане, проведённой к одной из них.
Вариант 6
-
Построить биссектрису и высоту треугольника, проведённые из одной вершины.
-
Построить равнобедренный прямоугольный треугольник по высоте, опущенной на гипотенузу.
Вариант 7
-
Построить треугольник АВС по сторонам АС = 3 см, ВС = 5 см, и С =50°.
-
На данной окружности найдите точки, равноудалённые от концов данной хорды.
Вариант 8
-
Построить угол, равный данному
-
На окружности с центром О выбрана точка А. Найдите точки окружности, равноудалённые от точек О и А.
Вариант 9
-
Построить углы 60° и 30°.
-
Найдите центр окружности, вписанной в ∆АВС.
Вариант 10
-
Разделить данный отрезок пополам.
-
Постройте окружность, вписанную в ∆АВС, если С=90°.
Литература
-
Атанасян Л.С. Бутузов В.Ф. Кадомцев С.Б. и др. Геометрия.7-9 класы: учеб. для общеобразоват. Учреждений. – М.: Просвещение, 2016. – 383 с.
-
Мельникова Н.Б Захарова Г.А. Дидактические материалы по геометрии к учебнику Л.С. Атанасян и др. «Геомертия 7-9 класссы». – М.: Издательство «Экзамен», 2013.- 143 с
-
Погорелов А.В Геометрия. 7-9 классы. – М.: Просвещение, 2010.- 224с.
-
Ершова А.П. Сборник заданий для тематического и итогового контроля знаний. Геометрия 7 класс. – М.: ИЛЕКСА, - 2013, - 112с
-
Мерзляк А.Г. В.Б. Полонский. Якир М.С. Геометрия 7 класс. Учеб. для учащихся общеобразовательных организаций – М.: Вентана-Граф, 2015. – 192с
52











 СО Найдите СОD.
СО Найдите СОD.





















 Треугольник DОВ – равнобедренный, ВD – его основание, DК и ВМ – медианы. Докажите, что:
Треугольник DОВ – равнобедренный, ВD – его основание, DК и ВМ – медианы. Докажите, что: Треугольник АВС – равнобедренный, АС – его основание, СD и АЕ – биссектрисы. Докажите, что:
Треугольник АВС – равнобедренный, АС – его основание, СD и АЕ – биссектрисы. Докажите, что: 















 ) 3 = 5;
) 3 = 5;





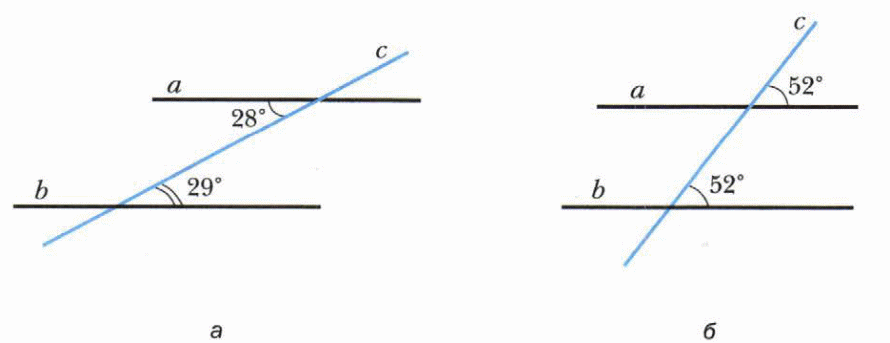



















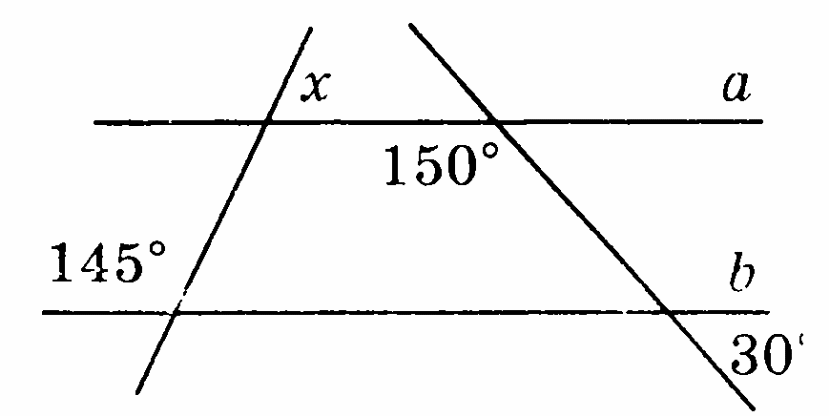







 = 15см. Докажите, что А B
= 15см. Докажите, что А B




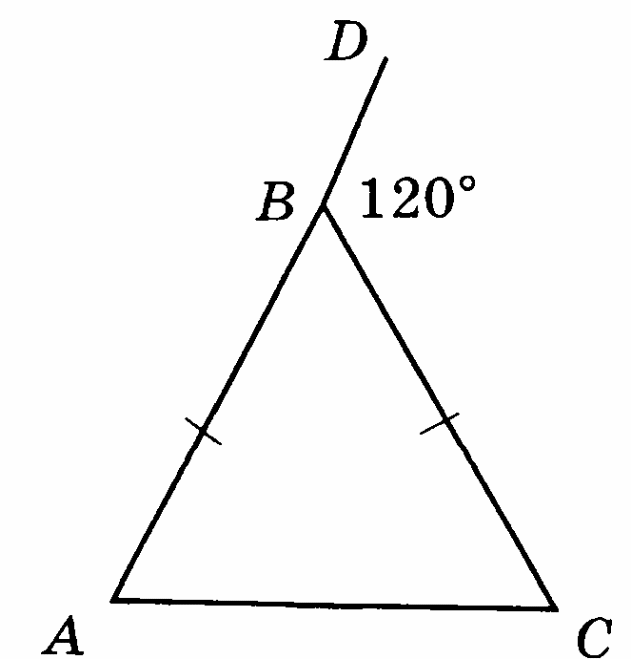










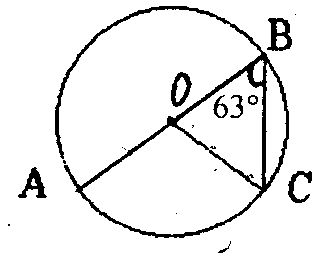



 . Постройте равнобедренный треугольник с боковой стороной, равной b, и углом, противолежащим основанию, равным
. Постройте равнобедренный треугольник с боковой стороной, равной b, и углом, противолежащим основанию, равным