Тема: Сандык удаалаштыктар, түрлөрү.
Сандык удаалаштыктын аныктамасы.
Сандык удаалаштыктын мүчөлөрү.
Сандык удаалаштыктын n - мүчөсүнүн формуласы.
Удаалаштыктардын түрлөрү. Рекурренттик формула.
Аныктама. Кандайдыр бир эреже же тартип менен жазылган сандардын катарын сан удаалаштыгы деп айтабыз.
Мисалы, 2; 4; 6; 8; …
1; 1; 1; 1; …
-7; -3; 0; 2; 9; …
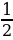 ;
; 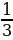 ;
; 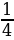 ;
; 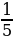 ; …
; …
Удаалаштыкты түзүүчү сандар удаалаштыктын мүчөлөрү деп аталат. Удаалаштыктын мүчөсү ал өзү турган катардагы номери менен айтылат. Мисалы, 2; 4; 6; 8; …удаалаштыгынын биринчи мүчөсү 2 ге барабар, экинчи мүчөсү 4 кө, үчүнчү мүчөсү 6 га барабар ж.б.у.с. Адатта удаалаштыктын мүчөлөрүн мүчөнүн катар номерин көрсөтүүчү индекс жазылган тамгалар менен белгилешет. Мисалы, 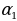 ,
, 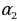 ,
, 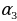 ,
, 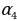 ж.б. Жалпысынан, удаалаштыктын n номерлүү мүчөсүн, же удаалаштыктын n- мүчөсүн
ж.б. Жалпысынан, удаалаштыктын n номерлүү мүчөсүн, же удаалаштыктын n- мүчөсүн 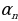 деп белгилешет. Удаалаштыктын өзүн
деп белгилешет. Удаалаштыктын өзүн 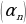 деп белгилейбиз.
деп белгилейбиз.
Удаалаштыктар өзүндө кармалган мүчөлөрүнүн санына жараша чектүү жана чексиз болуп экиге бөлүнөт. Мүчөлөрүнүн саны чектүү болгон удаа-лаштык чектүү удаалаштык деп аталат. Мисалы, 0,1; 0,4; 0,7; 1,2 удаалашты-гы чектүү удаалаштык болот, себеби бул удаалаштык төрт гана мүчөдөн турат. Ал эми мүчөлөрүнүн саны чексиз болгон удаалаштык чексиз удаалаш-тык деп аталат. Удаалаштыктарга мисал катары берилген удаалаштыктардын бардыгы чексиз удаалаштыктарга мисал болот.
Удаалаштыктар өзүндө кармалган мүчөлөрүнүн чоңдуктары боюнча жайгашуусуна жараша өсүүчү, кемүүчү жана турактуу болуп бөлүнүшөт. Мүчөлөрү чоңоюп баруучу удаалаштыктар өсүүчү удаалаштыктар деп ата-лат. Ал эми мүчөлөрү кичирейип баруучу удаалаштыктар кемүүчү удаалаш-тыктар деп аталат. Ал эми мүчөлөрү бир калыпта туруучу удаалаштыктар турактуу удаалаштыктар деп аталат. Мисалы, 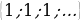 ж.б.
ж.б.
Көпчүлүк учурда удаалаштыкты, анын n–мүчөсүн n номеринен функ-ция катарында туюнтуучу формуланын жардамы менен беришет. Мындай формуланы удаалаштыктын n–мүчөсүнүн формуласы деп аташат. Мисалы, оң жуп сандардын удаалаштыгын 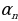 =2 n формуласы менен, алымы 1 ге барабар дурус бөлчөктөрдүн
=2 n формуласы менен, алымы 1 ге барабар дурус бөлчөктөрдүн 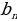 =
= 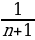 формуласы менен берүүгө болот.
формуласы менен берүүгө болот.
1-мисал. Удаалаштык 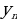 =
= 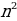 - 3n формуласы менен берилген. Анын алгачкы беш мүчөсүн тапкыла.
- 3n формуласы менен берилген. Анын алгачкы беш мүчөсүн тапкыла.
у1 =-2, у2 = -2, у3 = 0, у4 = 4, у5 = 10.
2-мисал. Удаалаштык хn = (-1)n 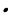 10 формуласы менен берилген. Удаа-лаштыктын мүчөлөрүн аныктагыла.
10 формуласы менен берилген. Удаа-лаштыктын мүчөлөрүн аныктагыла.
Бул удаалаштыктын бардык так номерлүү мүчөлөрү -10 го, ал эми жуп номерлүү мүчөлөрү 10 го барабар: х1 = -10, х2= 10, х3= -10, х4= 10, …
3-мисал. Удаалаштык сn= 5 формуласы менен берилген. Удаалаштык-тын мүчөлөрүн аныктагыла.
Бул удаалаштыктын бардык мүчөлөрү 5 ке барабар: с1=5, с2=5, с3=5, …
4-мисал. 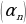 удаалаштыгынын биринчи мүчөсү 3 кө барабар, ал эми ар бир кийинки мүчө мурдагы мүчөнүн квадратына барабар, б.а.
удаалаштыгынын биринчи мүчөсү 3 кө барабар, ал эми ар бир кийинки мүчө мурдагы мүчөнүн квадратына барабар, б.а. 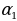 =3,
=3,
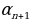 =
= 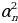 . Удаалаштыктын мүчөлөрүн аныктагыла.
. Удаалаштыктын мүчөлөрүн аныктагыла.
Натыйжада 3; 9; 81; 6561; … удаалаштыгын алабыз.
Удаалаштыктын кандайдыр мүчөсүнөн баштап каалагандай мүчөсүн андан мурда келүүчү мүчөлөр аркылуу туюнтулуучу формула рекурренттик формула деп аталат. Recurro деген латын сөзү, ал кыргызчага которгондо кайрылуу дегенди билдирет.
Өз алдынча иштөө үчүн тапшырмалар.
Ар бир мүчөсү анын үч эселенген номери менен бирдин айырмасына барабар болгон удаалаштыктын бешинчи, сегизинчи, элүүнчү мүчөлөрүн тапкыла. 20, 179, 1501 сандары ал удаалаштыктын мүчөлөрү болуп эсептелеби?
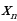 = 3n +2 формуласы менен берилген
= 3n +2 формуласы менен берилген 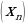 удаалаштыгы үчүн а)
удаалаштыгы үчүн а) 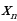
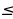 47; б)
47; б) 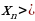 100; в) 80
100; в) 80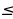
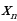
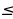 180 барабарсыздыгы туура болгондой мүчөлөрдүн номерлерин көрсөткүлө.
180 барабарсыздыгы туура болгондой мүчөлөрдүн номерлерин көрсөткүлө.
Эгер 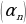 удаалаштыгы 5 ке бөлгөндө 1 калдык кала турган натуралдык сандардын удаалаштыгы болсо,
удаалаштыгы 5 ке бөлгөндө 1 калдык кала турган натуралдык сандардын удаалаштыгы болсо, 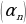 удаалаштыгынын алгачкы беш мүчөсүн жазгыла жана анын n–мүчөсүнүн формуласын түзгүлө.
удаалаштыгынын алгачкы беш мүчөсүн жазгыла жана анын n–мүчөсүнүн формуласын түзгүлө.
Эгер а) 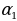 = 2,
= 2,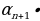
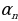 = 1; б)
= 1; б) 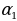 =5,
=5, 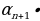
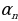 = -5; в)
= -5; в) 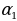 =1,
=1, 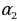 = 2,
= 2, 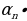
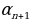
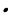
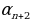 = 6 болсо,
= 6 болсо, 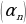 удаалаштыгыныналгачкы беш мүчөсүн жазгыла.
удаалаштыгыныналгачкы беш мүчөсүн жазгыла.
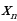 = 7 - 2n формуласы менен берилген
= 7 - 2n формуласы менен берилген 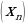 удаалаштыгынын - 61 ге барабар болгон мүчөсүнүн номерин тапкыла.
удаалаштыгынын - 61 ге барабар болгон мүчөсүнүн номерин тапкыла.
Төмөндөгү формула аркылуу берилген удаалаштыктын алгачкы алты мүчөсүн тапкыла: а) 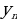 = 9 -
= 9 - 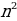 ; б)
; б) 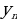 =
= 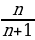 ; в)
; в) 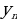 =
= 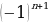 7.
7.







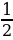 ;
; 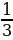 ;
; 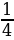 ;
; 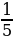 ; …
; …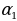 ,
, 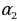 ,
, 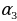 ,
, 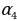 ж.б. Жалпысынан, удаалаштыктын n номерлүү мүчөсүн, же удаалаштыктын n- мүчөсүн
ж.б. Жалпысынан, удаалаштыктын n номерлүү мүчөсүн, же удаалаштыктын n- мүчөсүн 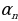 деп белгилешет. Удаалаштыктын өзүн
деп белгилешет. Удаалаштыктын өзүн 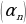 деп белгилейбиз.
деп белгилейбиз.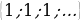 ж.б.
ж.б.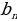 =
= 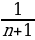 формуласы менен берүүгө болот.
формуласы менен берүүгө болот.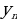 =
= 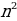 - 3n формуласы менен берилген. Анын алгачкы беш мүчөсүн тапкыла.
- 3n формуласы менен берилген. Анын алгачкы беш мүчөсүн тапкыла.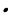 10 формуласы менен берилген. Удаа-лаштыктын мүчөлөрүн аныктагыла.
10 формуласы менен берилген. Удаа-лаштыктын мүчөлөрүн аныктагыла.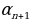 =
= 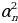 . Удаалаштыктын мүчөлөрүн аныктагыла.
. Удаалаштыктын мүчөлөрүн аныктагыла.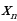 = 3n +2 формуласы менен берилген
= 3n +2 формуласы менен берилген 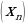 удаалаштыгы үчүн а)
удаалаштыгы үчүн а) 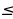 47; б)
47; б) 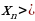 100; в) 80
100; в) 80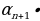
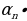
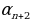 = 6 болсо,
= 6 болсо, 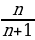 ; в)
; в) 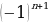 7.
7. 









