Для проведения и подготовки к итоговой контрольной работы за 6 класс, административной контрольной работы по итогам года, для проведения промежуточной аттестации можно использовать данные варианты заданий.
Их можно использовать для итогового повторения курса математики за 6 класс. А так же использовать для повторения в начале 7 класса.
Просмотр содержимого документа
«сборник вариантов контрольной (итоговой) работы в 6 классе»
Для проведения и подготовки к итоговой контрольной работы за 6 класс, административной контрольной работы по итогам года, для проведения промежуточной аттестации можно использовать данные варианты заданий.
Промежуточная итоговая аттестация по математике 6 класс
2015 – 2016 учебный год
Кодификатор элементов содержания по математике составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки учащихся 6 класса.
| Обозначение задания | Проверяемые элементы содержания и виды деятельности | Коды проверяемых элементов содержания и элементы содержания | Время выполнения |
| Часть 1 |
| 1 | Умение выполнять арифметические действия с десятичными дробями. | 1.1.14. Арифметические действия с десятичными дробями. | 3 |
| 2 | Владение понятием делимости натуральных чисел. | 1.1.4. Делимость натуральных чисел. Делители и кратные числа. Признаки делимости на 2, 3, 5, 9, 10. | 3 |
| 3 | Умение находить НОД и НОК. | 1.1.6. Простые числа. Разложение натурального числа на простые множители. | 3 |
| 4 | Умение применять основное свойство дроби. | 1.1.8. Основное свойство дроби. Сокращение дробей. | 2 |
| 5 | Умение выполнять действия с обыкновенными дробями. | 1.1.9. Арифметические действия с обыкновенными дробями. | 3 |
| 6 | Умение применять основное свойство пропорции. | 1.1.19. Основное свойство пропорции. | 3 |
| 7 | Умение находить модуль числа. | 1.1.25. Противоположные числа. Модуль числа, геометрический смысл модуля. | 2 |
| 8 | Умение распознавать пропорциональные и обратно пропорциональные величины. | 1.1.20. Пропорциональные и обратно пропорциональные величины. | 2 |
| 9 | Умение выполнять арифметические действия с положительными и отрицательными числами. | 1.1.27. Арифметические действия с положительными и отрицательными числами. Свойства арифметических действий. | 3 |
| 10 | Умение читать на координатной плоскости графики зависимости величин. | 4.4.1. Прямоугольная система координат на плоскости. 4.4.3. график функции. Чтение графиков. | 2 |
| Часть 2 |
| 1 | Умение преобразовывать буквенные выражения, выполнять числовые подстановки. | 2.2.1. Буквенные выражения. 2.2.2. Числовые подстановки в буквенные выражения. 2.2.7. Приведение подобных слагаемых. | 5 |
| 2 | Умение решать уравнения применяя общие приемы решения линейных уравнений с одним неизвестным | 3.3.1. Уравнение с одной переменной. Корни уравнения. | 5 |
| 3 | Умение решать текстовые задачи | 1.1.23. Решение текстовых задач арифметическими приемами. 3.3.10. Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом. | 20 |
Работа состоит из двух частей и содержит 13 заданий.
Часть 1 содержит 10 заданий обязательного уровня. К каждому заданию приведены 4 варианта ответа, из которых только один верный. При проверке базовой математической компетентности обучающиеся должны продемонстрировать: владение основными алгоритмами; знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.); умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Часть 2 содержит 3 более сложных задания, направленных на проверку владения материалом на повышенном уровне. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть учащихся, составляющую потенциальный контингент группы А классов при предметно поточном обучении. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности – от относительно простых до сложных, предполагающих свободное владение материалом курса и хороший уровень математической культуры.
Таблица количества баллов за выполненные задания
| Максимальное количество баллов за 1 задание | Количество баллов за работу в целом |
| Часть 1 | Часть 2 |
| Задания № 1 - 10 | Задания № 1 - 2 | Задание № 3 |
|
| 1 балл | 2 балла | 4 балла | 18 баллов |
Таблица перевода тестовых баллов в школьные оценки
| Тестовый балл | Школьная оценка |
| 0 – 4 | «2» |
| 5 – 9 | «3» |
| 10 – 13 | «4» |
| 14 – 18 | «5» |
Демо версия
Вариант 1
Часть 1
Выполните действия: 0,256 : 0,8 + 1,2 ∙ 0,01.
0,332 2) 0,44 3) 1,52 4) 4,52
Укажите числа, кратные 9, удовлетворяющие неравенству: 142 у ≤ 153.
149, 154 2) 144, 152 3) 145, 150 4) 144, 153
Найдите наибольший общий делитель чисел 324 и 432.
81 2) 108 3) 54 4) 162
Укажите при каких значениях п верно равенство
80 2) 12 3) 24 4) 3
Найдите значение выражения: (
3 2) 1 3) 4)
Найти неизвестный член пропорции 2,5 : 3,4 = х : 17
1,25 2) 23,12 3) 20 4) 12,5
Найдите значение выражения: + 3, если х = - 1
1 2) 4 3) 3 4) 3
Два одинаковых трактора вспахивают поле за 6 часов. За сколько часов вспашут это поле 4 таких же трактора?
24 2) 12 3) 3 4) 1,5
Вычислите: ( - 4 + 3 ) ∙ ( - 14).
– 0,5 2) – 30 3) 15 4) – 15
По графику определите координаты точки пересечения прямых АВ И СК.
(3;2) 2) (- 3; 0) 3) (2;3) 4) (0; - 2)
Часть 2
Упростите выражение 10а + в – 5а – 3в +7, найдите его значение, если а = 2, в = .
Решите уравнение: х – 0,2 = х + 0,85.
В первой пачке было в 2,2 раза больше тетрадей, чем во второй. После того, как из первой пачки взяли 27 тетрадей, а из второй 3 тетради, то в первой пачке стало в 2 раза меньше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке первоначально?
Варианты для подготовки к контрольной работе или их можно использовать для итогового повторения курса математики за 6 класс. А так же использовать для повторения в начале 7 класса.
Вариант 2
Часть 1
Выполните действия: 0,02976 : 0,024 + 0,296 ∙ 2,5.
3,96 2) 176,2 3) 1,98 4) 4,2
Укажите числа, кратные 3, удовлетворяющие неравенству: 123 ≤ у 132.
123,126,129 2) 123,126,132 3) 120,123,126 4) 123,125,129
Найдите, сколько простых множителей имеет наибольший общий делитель чисел 70 и 105.
1 2) 2 3) 3 4) 4
Запишите число в виде натурального числа
56 2) 169 3) 13 4) 26
Найдите значение выражения: (
4,3 2) 3,4 3) 4 4) 3
Решите уравнение: 12,3 : 6 = (7х) : (-4,2)
1,23 2) -12,3 3) 12,3 4) -1,23
Найдите значение выражения: , если k = 4
2) 7 3) -2,72 4) 4
Автомобиль на 113,6 км пути затратил 8,52 литра бензина. Сколько литров бензина потребуется ему, чтобы проехать 150 км?
11,2 2) 11,25 3) 112,5 4) 20
Вычислите: ( 5 - 7 ) :
2 2) –15 3) -2 4) 1,5
По графику определите точку, абсцисса которой равна 5.
A 2) B 3) C 4) D
Часть 2
Упростите выражение -5 , найдите его значение, если z = - .
Решите уравнение: -2
Масса зайца на 0,6 кг больше массы кролика, если масса зайца увеличится в 1,2 раза, а масса кролика – в 1,4 раза, то их массы станут равными. Какова масса зайца?
Вариант 3
Часть 1
Выполните действия: 48,168 : ( 0,56 + 1,6) ∙ 0,01.
4,816 2) 0,223 3) 48,16 4) 6,4
Укажите числа, кратные 2, удовлетворяющие неравенству: 200 ≤ у 204.
202,203 2) 200,204 3) 202,204 4) 201,207
Найдите наименьшее общее кратное чисел 212 и 318.
106 2) 636 3) 159 4) 424
Укажите, при каком значении с верно равенство:
14 2) 5 3) 28 4) 40
Найдите значение выражения: (
2) 3) 4)
Найдите неизвестный член пропорции: =
0.18 2) 0,5 3) 0,6 4) 1,8
Найдите y, если :
2) - 3) -4 4) 4
На пошив 9 рубашек ушло 18,9 метров ткани. Сколько таких рубашек можно сшить из 44,1 метра такой ткани?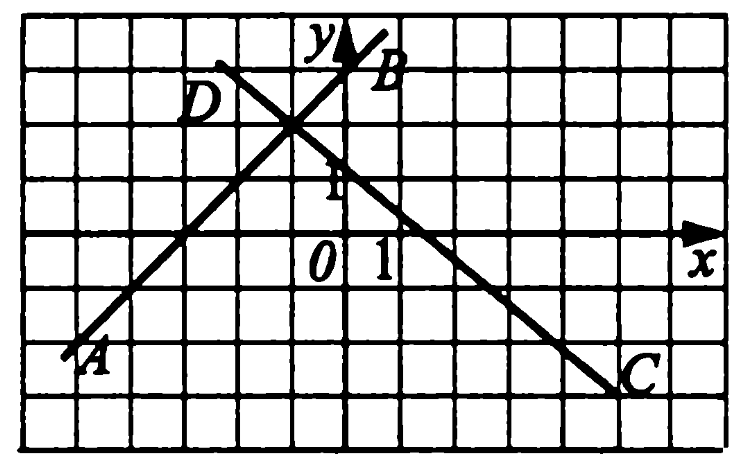
21 2) 92 3) 42 4) 18
Вычислите: ( -10)
21 2) –21 3) 19 4) -19
По графику определите координаты точки пересечения прямых АВ и CD.
(1; 3) 2) (-1; 2) 3) (2; -1) 4) (-1; -2)
Часть 2
Упростите выражение 7m + 3n – m - 8n - 11, найдите его значение, если m = 3, n = .
Решите уравнение: 1,2
В первом мешке было в 4 раза меньше муки, чем во втором. Если из первого мешка пересыпать во второй 20 кг, а затем из второго отсыпать в первый 50 кг, то в обоих мешках муки будет поровну. Сколько килограммов муки было в каждом мешке первоначально?
Вариант 4
Часть 1
Выполните действия: 72,4 ∙ 0,1- 27,36 : 7,6.
108,4 2) 68,76 3) 3,64 4) 10,84
Укажите числа, кратные 5, удовлетворяющие неравенству: 147 ≤ х 155.
140, 145 2) 145, 150 3) 150, 155 4) 145, 155
Найдите наибольший общий делитель чисел 231 и 273.
21 2) 31 3) 77 4) 39
Укажите, при каком значении b верно равенство:
12 2) 4 3) 63 4) 24
Найдите значение выражения: (
5 2) 3) 4) 18
Найдите неизвестный член пропорции: =
2 2) 0,5 3) 1 4) 0,2
Найдите х, если :
2) -3 3) 3 4)
6 труб заполняют бассейн водой за 24 минуты. Сколько таких труб достаточно, чтобы наполнить бассейн за 36 минут?
8 2) 5 3) 9 4) 4
Вычислите: ( -6)
-7 2) 14 3) -14 4) 7
По графику определите координаты точки пересечения прямых MN и KE.
(0; -2) 2) (2; 0) 3) (-2; 0) 4) (0; 2)
Часть 2
Упростите выражение 12c – 8d – 5c + 3d + 3, найдите его значение, если d = 3, c = .
Решите уравнение:
В двух контейнерах было одинаковое количество моркови. Когда из первого контейнера переложили 25 кг во второй, а затем во второй добавили еще 10 кг, то в нем оказалось в 4 раза больше моркови, чем в первом. Сколько килограммов моркови стало в каждом контейнере?
Вариант 5
Часть 1
Выполните действия: 4,7 : 125 – 1,26 ∙0,01.
0,025 2) 0,25 3) 2,5 4) 25
Между какими ближайшими натуральными числами, кратными 3, заключено число 32?
33; 36 2) 27; 30 3) 30; 33 4) 30; 36
Найдите наибольший общий делитель чисел 680 и 612.
17 2) 68 3) 34 4) 612
Укажите, при каком значении m верно равенство:
12 2) 80 3) 3 4) 40
Найдите значение выражения:
2) 4 3) 4 4) -4
Найдите неизвестный член пропорции: =
5,5 2) 5 500 3) 550 4) 0,55
Найдите значение выражения если a =
2) - 3) 4)
Для изготовления 15 деталей потребовалось 4,5 кг металла. Сколько таких деталей можно сделать из 6 кг этого металла?
20 2) 10 3) 15 4) 30
Вычислите:
2) 3) -2,4 4) 12,4
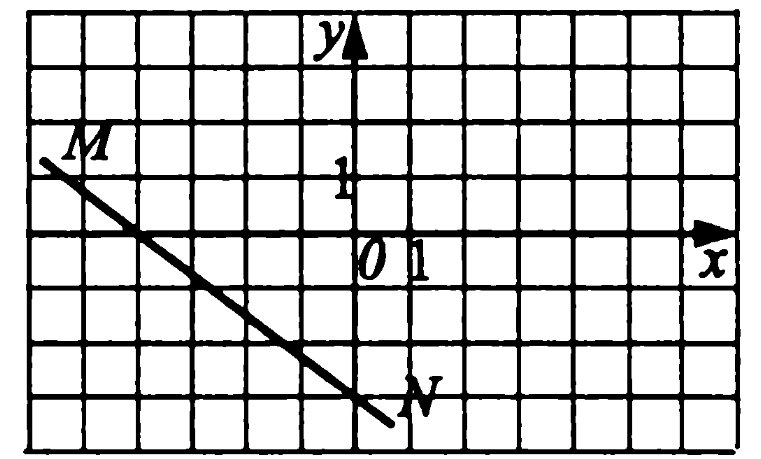
По графику определите координаты точки пересечения прямой MN c осью ординат.
(0; -3) 2) (-3; 0) 3) (-4; 0) 4) (0; -4)
Часть 2
Упростите выражение -3x + 7y + 13x – 7y - 3, найдите его значение, при x = 3,1, y= -15,01.
Решите уравнение: ( -
Школьники совершили трехдневный поход. В первый день было пройдено 80% того расстояния, которое прошли во второй день, а в третий – в 1,5 раза больше, чем во второй. Сколько км пути было пройдено в первый день? если за 3 дня школьники прошли 33 км?
Вариант 6
Часть 1
Выполните действия: (8,7∙20,4 – 17,64): 4,5.
35,52 2) 355,2 3) 3,552 4) 177,48
Укажите все нечетные числа, кратные 3, заключенные между числами 481 и 490.
1) 483; 484 2) 482; 484; 485; 3) 483; 489 4) 483; 485; 489
Найдите наибольший общий делитель чисел 150 и 175.
1) 25 2) 5 3) 125 4) 150
Приведите дробь к знаменателю 51.
2) 3) 4)
Найдите значение выражения:
2) 1 3) 5 4) 2
Найдите неизвестный член пропорции: а : 1,8 = 4,9 : 3,6
2,45 2) 3,5 3) 0,7 4) 5,4
Найдите значение выражения если a = - 2 .
1) 2) – 4 3) - 4)
На участке водопровода старые трубы длиной 5 м заменили на новые трубы длиной 8 м. Сколько нужно новых труб для замены 160 старых?
80 2) 60 3) 100 4) 120
Вычислите: 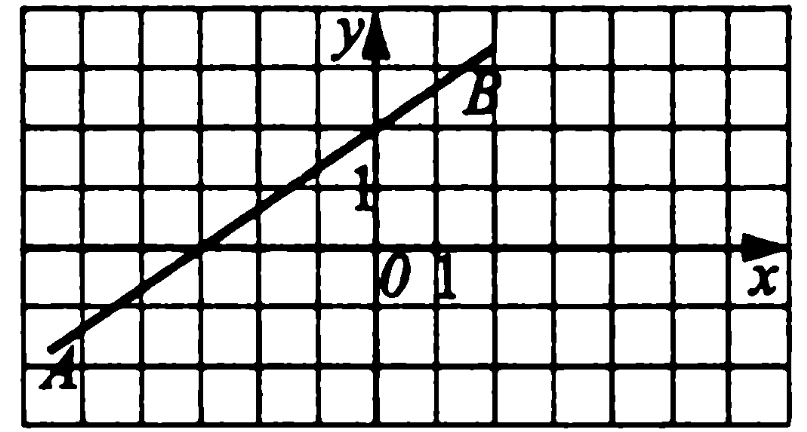
2) 2 3) - 2 4) - 3
По графику определите координаты точки пересечения прямой АВ c осью абсцисс.
(0; -3) 2) (0; 2) 3) (3; 0) 4) (- 3; 0)
Часть 2
Упростите выражение -5а – 8в + 13а + 8в – 7 , найдите его значение, при а = - 1, в = 1,01.
Решите уравнение: ( - 0,01х – 4,9) 758,1 = 0
Два велосипедиста выехали одновременно из одного города в другой. Первый ехал со скоростью 12 км/ч и приехал на место на два часа раньше второго, скорость которого 9 км/ч. Найдите расстояние между городами.
Вариант 7
Часть 1
Выполните действия: 10,1∙ (30,7 – 0,6447: 0,21).
0 2) 279,063 3)27,9063 4) 2790,63
Какие из данных чисел:9; 108; 1257; 333; 33333; 5533 – делятся на 3, но не делятся на 9?
1) 108; 1257 2) 9; 5533 3) 1257; 33333 4) 9; 108
Найдите наибольший общий делитель чисел 380 и 378.
1) 19 2) 2 3) 38 4) 63
Укажите, при каком значении р верно равенство:
1 2) 2 3) 7 4) 6
Найдите значение выражения:
2) 3) 6 4) 3
Найдите неизвестный член пропорции: х : 3,6 = 175 : 7
1) 90 2) 9 3) 150 4) 0,9
Найдите значение выражения 2х + если х = - 2 .
1) 2) – 2 3) 7 4) – 7
Из 39 кг свежих слив выходит 10,5 кг сушеных. Сколько свежих слив нужно взять, чтобы получить 31,5 кг сушеных?
130 2) 345 3) 117 4) 94,5
Вычислите: 
2) - 1 3) - 15 4) 15
По графику определите координаты точки пересечения прямых PQ и EF.
1)(-6; 3) 2) (- 3; 3) 3) (- 3; 0) 4) (- 6; 0)
Часть 2
Упростите выражение -1,1а + 8,3в + 1,1а – 9,3в + 1, найдите его значение, при а = 15,7, в = - 7 .
Решите уравнение: - 9,2∙ ( -
В одном зоопарке было в 4 раза меньше обезьян, чем в другом. Когда из второго зоопарка в первый перевезли 12 обезьян, то обезьян в зоопарк стало поровну. Сколько обезьян было в каждом зоопарке первоначально?























