Задачи на второй закон Ньютона.
(МФТИ. Заключительный этап 2018 год. 9 класс. В1.)
 На гладкой горизонтальной поверхности расположена доска массой 2m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 2m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
1) Какую минимальную горизонтальную силу Fмин надо приложить к бруску, чтобы он начал двигаться относительно доски?
2) За какое время брусок переместится относительно доски на расстояние L, если к нему приложить силу FFмин?
(МФТИ. Заключительный этап 2018 год. 9 класс. В2.)
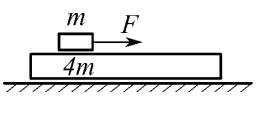 На гладкой горизонтальной поверхности расположена доска массой 4m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 4m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
1) Какую минимальную горизонтальную силу Fмин надо приложить к бруску, чтобы он начал двигаться относительно доски?
2) За какое время брусок переместится относительно доски на расстояние L, если к нему приложить силу FFмин?
(МФТИ. Заключительный этап 2018 год. 9 класс. В4.)
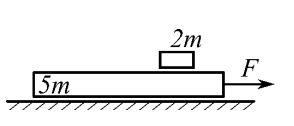 На гладкой горизонтальной поверхности расположена доска массой 5m, на которой лежит брусок массой 2m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 5m, на которой лежит брусок массой 2m. Коэффициент трения между бруском и доской µ.
1) Какую минимальную горизонтальную силу Fмин надо приложить к доске, чтобы относительно неё начал двигаться брусок?
2) За какое время брусок переместится относительно доски на расстояние L, если к доске приложить силу FFмин.
(МФТИ. Заключительный этап 2019 год. 9 класс. В1.)
Цилиндрический сосуд с водой стоит на весах. Показание весов P1 =10 Н. В воду опустили льдинку с вмороженным в нее металлическим шариком. Уровень воды в сосуде повысился на h 4 см, а льдинка стала плавать, полностью погрузившись в воду, не касаясь дна и стенок.
Плотность воды 1000 кг/м3, плотность льда 1 0,9 , плотность металла 2 2,7, площадь поперечного сечения сосуда S 100см2. Ускорение свободного падения g 10 м/с2.
1) Найдите показание P2 весов после погружения в сосуд льдинки.
2) Найдите массу m1 льда.
3) Изменится ли показание весов после таяния льда? Ответ обоснуйте.
(МФТИ. Заключительный этап 2019 год. 9 класс. В2.)
Цилиндрический сосуд с водой стоит на весах. В воду опустили льдинку с вмороженным в нее металлическим кубиком. Льдинка стала плавать, полностью погрузившись в воду, не касаясь дна и стенок. Уровень воды в сосуде повысился на h 8 см, показание весов стало равным P 20 Н.
Плотность воды 1000 кг/м3, плотность льда 1 0,9 , плотность металла 2 2,3 , площадь поперечного сечения сосуда S 75 см2. Ускорение свободного падения g 10 м/с2.
1) Найдите массу M сосуда с водой до погружения льдинки.
2) Найдите массу m2 металлического кубика.
3) Изменится ли показание весов после таяния льда? Ответ обоснуйте.
(МФТИ. Заключительный этап 2019 год. 9 класс. В3.)
На заснеженном склоне с углом наклона α к горизонту коэффициент трения скольжения лыжника на высотах меньших h равен µ1 (µ1 tgα), на больших высотах коэффициент трения скольжения лыжника равен µ2 (µ2
1) С какой высоты H следует стартовать лыжнику с нулевой начальной скоростью, чтобы доехать до основания склона с нулевой конечной скоростью?
2) Найдите максимальную скорость VMAX лыжника.
3) Найдите продолжительность T движения на участке торможения.
(МФТИ. Заключительный этап 2019 год. 9 класс. В3.)
На наклонной плоскости с углом наклона α к горизонту коэффициент трения скольжения шайбы по плоскости на высотах меньших некоторой неизвестной высоты h равен µ1 (µ1 tgα), на больших высотах коэффициент трения скольжения шайбы равен µ2 (µ2
1) Найдите высоту h.
2) Найдите максимальную скорость VMAX шайбы в процессе движения.
3) Найдите продолжительность T движения на участке разгона.
(МФТИ. Заключительный этап 2020 год. 9 класс. В3.)
Чтобы спускать брусок равномерно по наклонной плоскости с углом наклона 300 к горизонту, следует приложить силу F1, направленную вверх вдоль наклонной плоскости, а чтобы равномерно втаскивать брусок вверх, следует приложить такую же по направлению силу F2.
1) Найдите коэффициент трения скольжения бруска по плоскости, если F2=2F.
2) Какую по величине V0 скорость, направленную вверх вдоль наклонной плоскости, следует сообщить бруску, чтобы он остановился на расстоянии S 1,35 м от точки старта? Ускорение свободного падения g 10 м/c2
(МФТИ. Заключительный этап 2020 год. 9 класс. В4.)
Чтобы спускать брусок равномерно по наклонной плоскости, следует приложить силу F1, направленную вверх вдоль наклонной плоскости, а чтобы равномерно втаскивать брусок вверх, следует приложить такую же по направлению силу 𝐹2 = 1,5𝐹1. Коэффициент трения скольжения бруска по плоскости 0,2. Наклонная плоскость образует с горизонтальной плоскостью угол .
1) Найдите tg .
2) Какую по величине V0 начальную скорость, направленную вверх вдоль наклонной плоскости, следует сообщить бруску, чтобы через T 0,5 с брусок остановился?
Ускорение свободного падения g 10 м/c2.
(МФТИ. Заключительный этап 2021 год. 9 класс. В3.)
На железнодорожной платформе, движущейся по горизонтальному рельсовому пути с постоянной по величине и направлению скоростью V0 10 м/с, стоит коробка. Внезапно начинается торможение, платформа движется по прямой до полной остановки с постоянным по величине ускорением a 2 м/с2. Коробка, в свою очередь, перемещается относительно платформы на S 12 м и останавливается. Ускорение свободного падения g 10 м/с2. Коробка движется по горизонтальной прямой.
1) Найдите тормозной путь L платформы.
2) Найдите коэффициент трения скольжения коробки.
3) В течение какого времени T скорость коробки в системе отсчета, связанной с платформой, увеличивалась?
4) Найдите наибольшую скорость UMAX коробки относительно платформы.
(МФТИ. Заключительный этап 2021 год. 9 класс. В4.)
В кузове автомобиля, движущегося по горизонтальной дороге с постоянной по величине и направлению скоростью V0 5 м/с, стоит коробка. Внезапно начинается торможение, автомобиль движется до полной остановки в течение времени T 4 с по прямой с постоянным ускорением. Коробка, в свою очередь, приходит в движение, перемещается на S 2,5 м относительно кузова и останавливается. Коробка движется по горизонтальной прямой.
1) Найдите тормозной путь L автомобиля.
2) Найдите ускорение a коробки в лабораторной системе отсчета.
3) В течение какого времени скорость коробки в системе отсчета, связанной с автомобилем, уменьшалась?
4) Найдите наибольшую скорость UMAX коробки в системе отсчета, связанной с автомобилем. Ускорение свободного падения g 10 м/с2.
(МФТИ. Заключительный этап 2016 год. 10 класс. В5.)
Маленький шарик массой m подвешен на нити и колеблется в вертикальной плоскости с угловой амплитудой 0 arccos0,8.
1) Найти минимальную силу натяжения нити при колебаниях
2) Найти максимальную силу натяжения нити при колебаниях.
3) Найти касательное ускорение шарика в момент, когда сила натяжения нити в 1,5 раза больше ее минимального значения.
(МФТИ. Заключительный этап 2016 год. 10 класс. В6.)
Маленький шарик массой m подвешен на нити и колеблется в вертикальной плоскости с угловой амплитудой 0 arccos0,75.
1) Найти минимальную силу натяжения нити при колебаниях
2) Найти максимальную силу натяжения нити при колебаниях.
3) Найти центростремительное ускорение шарика в момент, когда сила натяжения нити на 25% превышает ее минимальное значение.
(МФТИ. Заключительный этап 2018 год. 10 класс. В1.)
Пустую стеклянную бутылку опускают в цилиндрический сосуд с водой с вертикальными стенками. Бутылка стала плавать, а уровень воды в сосуде поднялся на H1=3 см. Затем в бутылку медленно наливают воду. Когда масса налитой воды достигает некоторой величины, бутылка начинает тонуть. Уровень воды в сосуде за время наливания поднялся ещё на H2=1 см. Плотность стекла 0 3 г/см3, плотность воды 1 г/см3. Площадь внутреннего сечения сосуда S=250 см2.
1) Найти массу пустой бутылки.
2) Найти массу воды, налитой в бутылку.
3) Найти вместимость пустой бутылки.
(МФТИ. Заключительный этап 2018 год. 10 класс. В2.)
Пустую стеклянную бутылку вместимостью V=0,8 л опускают в цилиндрический сосуд с водой с вертикальными стенками. Бутылка стала плавать, а уровень воды в сосуде поднялся на H1=2 см. Затем в бутылку медленно наливают воду. Когда масса налитой воды достигает некоторой величины, бутылка начинает тонуть. Уровень воды в сосуде за время наливания поднялся ещё на H2. Плотность стекла 0 2,5 г/см3, плотность воды 1 г/см3. Площадь внутреннего сечения сосуда S=250 см2.
1) Найти массу пустой бутылки.
2) Найти массу воды, налитой в бутылку.
3) Найти H2.
(МФТИ. Заключительный этап 2018 год. 10 класс. В4.)
Пустую стеклянную колбу массой m0 = 500 г опускают в цилиндрический сосуд с водой. Стенки сосуда вертикальны. Колба стала плавать, а уровень воды в сосуде поднялся на некоторую высоту H1. Затем в колбу медленно наливают воду. Когда масса налитой воды достигает m = 500 г, колба начинает тонуть. Уровень воды в сосуде за время наливания поднялся ещё на H2. Плотность воды 1 г/см3, плотность стекла 0 2,5 г/см3. Площадь внутреннего сечения сосуда S = 250 см2.
1) Найти H1.
2) Найти H2.
3) Найти вместимость пустой колбы.
(МФТИ. Заключительный этап 2019 год. 10 класс. В3.)
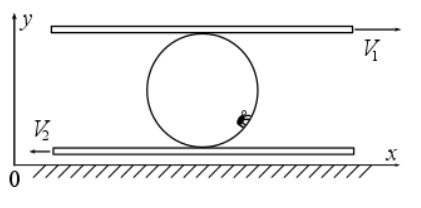 Тонкостенный полый шар радиуса R 0,1 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,6 м/с, а вторая - влево со скоростью V2 0,4 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 1 г. Ускорение свободного падения g 10 м/с2.
Тонкостенный полый шар радиуса R 0,1 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,6 м/с, а вторая - влево со скоростью V2 0,4 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 1 г. Ускорение свободного падения g 10 м/с2.
1) Найдите скорость V центра шара.
2) Найдите максимальную силу PMAX, с которой жук действует на шар.
(МФТИ. Заключительный этап 2019 год. 10 класс. В4.)
 Тонкостенный полый шар радиуса R 0,05 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,8 м/с, а другая - влево со скоростью V2 0, 2 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 2 г.
Тонкостенный полый шар радиуса R 0,05 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,8 м/с, а другая - влево со скоростью V2 0, 2 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 2 г.
1) За какое время T шар совершает один оборот вокруг горизонтальной оси, проходящей через его центр?
2) Найдите силу P, с которой жук действует на шар, в тот момент, когда жук находится в высшей точке траектории.
(МФТИ. Заключительный этап 2021 год. 10 класс. В3.)
Маленькая коробка съезжает по наклонной плоскости, образующей угол 300 с горизонтом. Коэффициент трения скольжения коробки по поверхности на высотах меньших h 2 м равен 1 0,81, на больших высотах коэффициент трения скольжения равен 2 0,11. Начальная скорость коробки нулевая. У основания наклонной плоскости коробка останавливается.
1) Найдите продолжительность T движения коробки на участке торможения.
2) С какой высоты H съехала коробка?
Ускорение свободного падения g 10 м/с2.
(МФТИ. Заключительный этап 2021 год. 10 класс. В4.)
Маленькая коробка съезжает по наклонной плоскости, образующей угол с горизонтом, такой, что cos 24/25. Коэффициент трения скольжения коробки по поверхности на высотах меньших h 1, 4 м равен 1 0,5 , на больших высотах коэффициент трения скольжения равен 2 0,06. Начальная скорость коробки нулевая. У основания наклонной плоскости коробка останавливается.
1) Найдите наибольшую скорость VMAX коробки в процессе движения.
2) Найдите путь S, пройденный коробкой от старта до остановки. Ускорение свободного падения g 10 м/с2.
(МФТИ. Заключительный этап 2022 год. 10 класс. В1.)
По внутренней поверхности проволочной металлической сферы радиуса R = 1,2 м равномерно со скоростью V0 = 3,7 м/с движется модель автомобиля. Движение происходит в горизонтальной плоскости большого круга. Масса модели m = 0,4 кг. Модель приводится в движение двигателем. Силу сопротивления считайте пренебрежимо малой.
1) С какой по величине силой P модель действует на сферу?
2) Рассмотрим модель автомобиля равномерно движущуюся по окружности в плоскости большого круга, составляющей с горизонтом угол = /6. Вычислите минимальную допустимую скорость VMIN такого равномерного движения. Коэффициент трения скольжения шин по поверхности сферы = 0,9.
Ускорение свободного падения g=10 м/с2.
(МФТИ. Заключительный этап 2022 год. 10 класс. В2.)
По внутренней поверхности проволочной сферы равномерно движется модель автомобиля. Движение происходит в горизонтальной плоскости большого круга. Сила, с которой модель действует на сферу, в два раза больше силы тяжести, действующей на модель. Модель приводится в движение двигателем. Силу сопротивления считайте пренебрежимо малой.
1) Найдите ускорение a модели.
2) Вычислите минимальную допустимую скорость VMIN равномерного движения модели по окружности в плоскости большого круга, составляющей с горизонтом угол = 450. Коэффициент трения скольжения шин по поверхности сферы = 0,8, радиус сферы R =1 м. Ускорение свободного падения g=10 м/с2.
(МФТИ. Заключительный этап 2022 год. 10 класс. В3.)
Модель автомобиля равномерно движется по окружности радиуса R =1,2 м, лежащей в горизонтальной плоскости. Модель приводится в движение двигателем. Коэффициент трения скольжения шин модели по поверхности = 0,8.
Ускорение свободного падения g =10 м/с2. Силу сопротивления считайте пренебрежимо малой.
1) За какое минимальное время T автомобиль может проехать четверть окружности? Модель помещают на наклонную поверхность, составляющую угол = 300 с горизонтом.
2) Найдите максимальную скорость VMAX, равномерного движения модели по окружности радиуса R =1,2 м на наклонной поверхности. Коэффициент трения скольжения шин модели по поверхности = 0,8.
(МФТИ. Заключительный этап 2022 год. 10 класс. В4.)
Максимальная скорость движения модели автомобиля по окружности радиуса R = 2 м, лежащей в горизонтальной плоскости, равна VMAX = 4 м/с. Модель приводится в движение двигателем. Ускорение свободного падения g =10 м/с2. Силу сопротивления считайте пренебрежимо малой.
1) Найдите коэффициент трения скольжения шин модели по поверхности. Модель помещают на наклонную поверхность, составляющую угол с горизонтом такой, что sin = 0,6.
2) Найдите наименьшее время T, за которое модель равномерно проедет по окружности радиуса R = 2 м на наклонной поверхности. Коэффициент трения скольжения шин модели по поверхности = 0,8.
(МФТИ. Заключительный этап 2023 год. 10 класс. В1.)
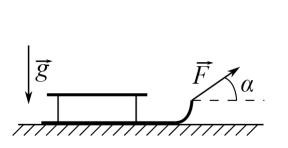 Санки дважды разгоняют из состояния покоя до одной и той же скорости V0 за одинаковое время. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения скорости 𝑉0 действие внешней силы прекращается.
Санки дважды разгоняют из состояния покоя до одной и той же скорости V0 за одинаковое время. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения скорости 𝑉0 действие внешней силы прекращается.
1) Найдите коэффициент 𝜇 трения скольжения санок по горизонтальной поверхности.
2) Через какое время 𝑇 после прекращения действия силы санки остановятся?
Ускорение свободного падения g. Санки находятся на горизонтальной поверхности. Движение санок прямолинейное.
(МФТИ. Заключительный этап 2023 год. 10 класс. В2.)
 Санки дважды разгоняют из состояния покоя до одной и той же кинетической энергии 𝐾 на одинаковых участках пути. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения кинетической энергии K действие внешней силы прекращается.
Санки дважды разгоняют из состояния покоя до одной и той же кинетической энергии 𝐾 на одинаковых участках пути. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения кинетической энергии K действие внешней силы прекращается.
1) Найдите коэффициент 𝜇 трения скольжения санок по горизонтальной поверхности.
2) Найдите перемещение 𝑆 санок в процессе торможения до остановки. Масса санок m.
Ускорение свободного падения g. Санки находятся на горизонтальной поверхности. Движение санок прямолинейное.
(МФТИ. Заключительный этап 2023 год. 10 класс. В3.)
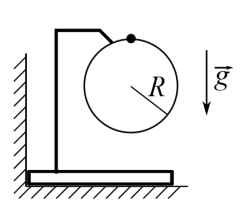 Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 1 м, на которое надет шарик. Массы бруска и шарика одинаковы. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.
Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 1 м, на которое надет шарик. Массы бруска и шарика одинаковы. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.
1) Найдите ускорение 𝑎 шарика в тот момент, когда сила, с которой брусок действует на вертикальную стенку, обращается в ноль. В ответе укажите модуль и направление вектора 𝑎.
2) Найдите вертикальное перемещение h шарика к этому моменту времени.
3) Найдите наибольшую скорость V бруска.
Все перемещения происходят в одной вертикальной плоскости. Ускорение свободного падения g = 10 м/с2. В процессе движения брусок не отрывается от гладкой горизонтальной плоскости.
(МФТИ. Заключительный этап 2023 год. 10 класс. В3.)
 Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 0,6 м, на которое надет шарик. Массы шарика и бруска одинаковы и равны 𝑚 = 0,2 кг. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.
Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 0,6 м, на которое надет шарик. Массы шарика и бруска одинаковы и равны 𝑚 = 0,2 кг. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.
1) Найдите равнодействующую 𝐹 сил, приложенных к шарику в тот момент, когда сила, с которой вертикальная стенка действует на брусок, обращается в ноль. В ответе укажите модуль 𝐹 и направление вектора 𝐹.
2) Найдите горизонтальное перемещение S шарика к этому моменту времени.
3) Найдите скорость V шарика в тот момент, когда скорость бруска наибольшая. Брусок безотрывно движется по гладкой горизонтальной плоскости.
Все перемещения происходят в одной вертикальной плоскости. Ускорение свободного падения g = 10 м/с2. В процессе движения брусок не отрывается от гладкой горизонтальной плоскости.
(МФТИ. Заключительный этап 2024 год. 10 класс. В1.)
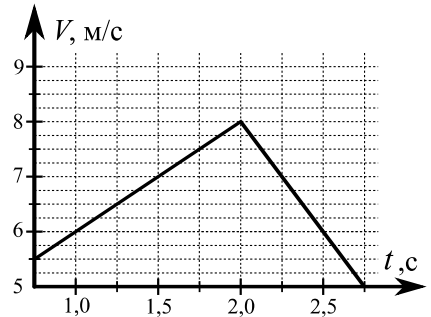 В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Шайба движется по плоскости, сталкивается с упором, отскакивает от него и продолжает движение по плоскости. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Шайба движется по плоскости, сталкивается с упором, отскакивает от него и продолжает движение по плоскости. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
1. Найдите sin 𝛼, здесь 𝛼 ‒ угол, который наклонная плоскость образует с горизонтом.
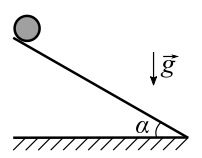 Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды равна массе бочки. Упор удален с наклонной плоскости. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды равна массе бочки. Упор удален с наклонной плоскости. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
2. С какой по величине скоростью 𝑉 движется бочка после перемещения по вертикали на h = 0,3 м?
3. Найдите ускорение 𝑎, с которым движется бочка.
4. При каких величинах коэффициента 𝜇 трения скольжения бочка катится без проскальзывания?
(МФТИ. Заключительный этап 2024 год. 10 класс. В2.)
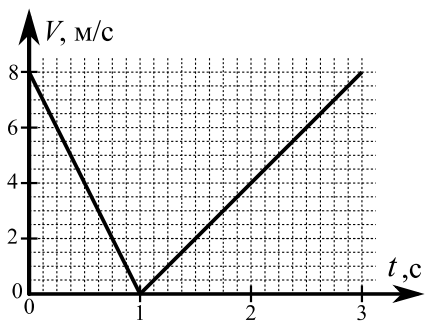 В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
1. Найдите sin 𝛼, здесь 𝛼 ‒ угол, который наклонная плоскость образует с горизонтом.
 Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды в n=2 раза больше массы бочки. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды в n=2 раза больше массы бочки. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
2. С какой по величине скоростью 𝑉 движется бочка после перемещения относительно наклонной плоскости на L=0,6 м?
3. Найдите ускорение 𝑎, с которым движется бочка.
4. При каких величинах коэффициента 𝜇 трения скольжения бочка катится без проскальзывания?
(МФТИ. Заключительный этап 2024 год. 10 класс. В5.)
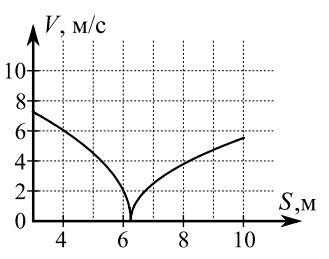 В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
Найдите ускорение 𝑎, c которым шайба движется до остановки.
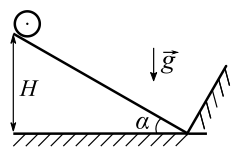 Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. После вертикального перемещения на H=1,6 м обруч сталкивается с гладкой стенкой.
Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. После вертикального перемещения на H=1,6 м обруч сталкивается с гладкой стенкой.
2. С какой по величине скоростью 𝑉 движется центр обруча сразу после абсолютно упругого соударения с гладкой стенкой?
3. Найдите перемещение L обруча при дальнейшем движении к тому моменту, когда скорость центра обруча станет равной нулю. В системе центра масс угловое ускорение обруча при скольжении |𝛥𝜔/𝛥𝑡| = 𝜇𝑔𝑐𝑜𝑠𝛼/𝑅. Коэффициенты трения скольжения шайбы и обруча по наклонной плоскости одинаковы. Радиус обруча 𝑅 ≪ 𝐻. Ускорение свободного падения g =10 м/c2.
(МФТИ. Заключительный этап 2024 год. 10 класс. В6.)
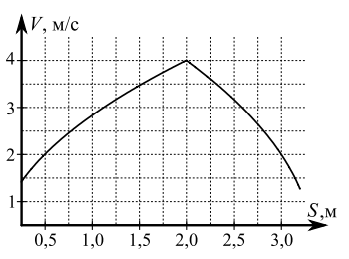 В первом опыте на шероховатую наклонную плоскость кладут шайбу, которая приходит в движение с нулевой начальной скоростью. Движение шайбы до и после соударения с гладкой стенкой, находящейся у основания наклонной плоскости, происходит вдоль одной и той же прямой. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче.
В первом опыте на шероховатую наклонную плоскость кладут шайбу, которая приходит в движение с нулевой начальной скоростью. Движение шайбы до и после соударения с гладкой стенкой, находящейся у основания наклонной плоскости, происходит вдоль одной и той же прямой. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче.
Найдите ускорение 𝑎, c которым шайба движется в процессе разгона.
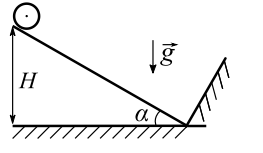 Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. Перед абсолютно упругим соударением с гладкой стенкой центр обруча движется со скоростью 𝑉 = 4 м/с.
Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. Перед абсолютно упругим соударением с гладкой стенкой центр обруча движется со скоростью 𝑉 = 4 м/с.
2. Найдите вертикальное перемещение H центра обруча за время движения от старта до столкновения с гладкой стенкой.
3. Через какое время T после столкновения с гладкой стенкой центр обруча будет находиться на максимальной высоте? В системе центра масс угловое ускорение обруча при скольжении | 𝛥𝜔/𝛥𝑡 | = 𝜇𝑔𝑐𝑜𝑠𝛼/𝑅. Коэффициенты трения скольжения шайбы и обруча по наклонной плоскости равны. Радиус обруча 𝑅 ≪ 𝐻. Ускорение свободного падения g =10 м/c2.







 На гладкой горизонтальной поверхности расположена доска массой 2m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 2m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.  На гладкой горизонтальной поверхности расположена доска массой 4m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 4m, на которой лежит брусок массой m. Коэффициент трения между бруском и доской µ.  На гладкой горизонтальной поверхности расположена доска массой 5m, на которой лежит брусок массой 2m. Коэффициент трения между бруском и доской µ.
На гладкой горизонтальной поверхности расположена доска массой 5m, на которой лежит брусок массой 2m. Коэффициент трения между бруском и доской µ.  Тонкостенный полый шар радиуса R 0,1 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,6 м/с, а вторая - влево со скоростью V2 0,4 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 1 г. Ускорение свободного падения g 10 м/с2.
Тонкостенный полый шар радиуса R 0,1 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,6 м/с, а вторая - влево со скоростью V2 0,4 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 1 г. Ускорение свободного падения g 10 м/с2.  Тонкостенный полый шар радиуса R 0,05 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,8 м/с, а другая - влево со скоростью V2 0, 2 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 2 г.
Тонкостенный полый шар радиуса R 0,05 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V1 0,8 м/с, а другая - влево со скоростью V2 0, 2 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m 2 г.  Санки дважды разгоняют из состояния покоя до одной и той же скорости V0 за одинаковое время. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения скорости 𝑉0 действие внешней силы прекращается.
Санки дважды разгоняют из состояния покоя до одной и той же скорости V0 за одинаковое время. В первом случае санки тянут, действуя постоянной по модулю силой, направленной под углом 𝛼 к горизонту (см. рис.). Во втором случае такая же по модулю сила, приложенная к санкам, направлена горизонтально. После достижения скорости 𝑉0 действие внешней силы прекращается.  Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 1 м, на которое надет шарик. Массы бруска и шарика одинаковы. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.
Брусок установлен вплотную к вертикальной стенке (см. рис.). На бруске закреплено в вертикальной плоскости кольцо радиуса 𝑅 = 1 м, на которое надет шарик. Массы бруска и шарика одинаковы. Кольцо и держатель легкие. Трения нет. Из верхней точки кольца шарик скользит с пренебрежимо малой начальной скоростью.  В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Шайба движется по плоскости, сталкивается с упором, отскакивает от него и продолжает движение по плоскости. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Шайба движется по плоскости, сталкивается с упором, отскакивает от него и продолжает движение по плоскости. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.  Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды равна массе бочки. Упор удален с наклонной плоскости. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды равна массе бочки. Упор удален с наклонной плоскости. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.  В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от времени представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.  Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды в n=2 раза больше массы бочки. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.
Во втором опыте с той же наклонной плоскости скатывается без проскальзывания тонкостенная однородная цилиндрическая бочка, полностью заполненная водой. Начальная скорость нулевая. Масса воды в n=2 раза больше массы бочки. Воду считайте идеальной жидкостью. Масса торцов бочки пренебрежимо мала.  В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.
В первом опыте на шероховатую наклонную плоскость кладут шайбу и сообщают шайбе начальную скорость. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче. Движение шайбы до и после остановки происходит вдоль одной и той же прямой. Ускорение свободного падения g =10 м/c2.  Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. После вертикального перемещения на H=1,6 м обруч сталкивается с гладкой стенкой.
Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. После вертикального перемещения на H=1,6 м обруч сталкивается с гладкой стенкой.  В первом опыте на шероховатую наклонную плоскость кладут шайбу, которая приходит в движение с нулевой начальной скоростью. Движение шайбы до и после соударения с гладкой стенкой, находящейся у основания наклонной плоскости, происходит вдоль одной и той же прямой. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче.
В первом опыте на шероховатую наклонную плоскость кладут шайбу, которая приходит в движение с нулевой начальной скоростью. Движение шайбы до и после соударения с гладкой стенкой, находящейся у основания наклонной плоскости, происходит вдоль одной и той же прямой. Часть зависимости модуля скорости шайбы от пройденного пути представлена на графике к задаче.  Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. Перед абсолютно упругим соударением с гладкой стенкой центр обруча движется со скоростью 𝑉 = 4 м/с.
Во втором опыте однородный обруч скатывается с той же наклонной плоскости без проскальзывания (см. рис.). Начальная скорость нулевая. Перед абсолютно упругим соударением с гладкой стенкой центр обруча движется со скоростью 𝑉 = 4 м/с. 









