Сборник задач со спичками

МБОУ «Юнкюрская СОШ имени В.И.Сергеева» Олекминского района РС(Я)

Сборник задач и головоломок со спичками

Составитель:

Солдатова Т.П., учитель математики

с. Юнкюр 2016 год

Глава 1. Числа и цифры.

Исправить ошибку в уравнении, передвинув только одну спичку:

1. XI - V = IV
   

2. VI = IV - III

1. XIV - V = XX

1. IX - IX = V

1. X = VIII – II

1. VII = I

1. L + L = L

1. Передвиньте 1 спичку так, чтобы получилось правильное уравнение.
   
   
   

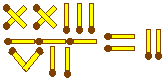
1. VI - IV = IX

2. VI - IV =XI

3. VI + IV = XII

4. X + X = I

5. X - IX = VI

6. VIII + IV = XVII

7. IX + VI = X

8. VII = X - III

9. IX - VI = XI

10. V = II + VIII

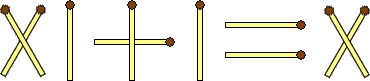
11. Переставьте одну спичку, чтобы пример имел решение I + I = XII

12. IIII = II

13. XI + I = X

14. III=I

15. II - I = II

16. III= II - I

17. I = II = III

18. VII = V - I

19. II - IIII = II

20. III + I = I – I

21. XI + V = V

22. VII + III = V

23. IVI - III = IX

24. XIII = VII - VI

25. VIII + IV = XVII

1. 

1. Используя одну дополнительную спичку, добейтесь верного равенства

5 + 5 +5 = 550

1. Переложите две спички так, чтобы равенство стало верным VI + X = III

1. В каждом из трех горизонтальных рядов переложите по одной спичке так, чтобы шесть равенств (вертикальных и горизонтальных) оказались верными

XIII : II = IV

: : :

V : III = III

= = =

III : I = I

1. В каждом из трех горизонтальных рядов переложите по одной спичке так, чтобы шесть равенств (вертикальных и горизонтальных) оказались верными

VI ∙ III = VII

∙ ∙ ∙

II ∙ IV = V

= = =

V ∙ VIII = XXXIII

1. Из пяти спичек сделайте шесть.

1. Из 5 спичек сделайте 8.

1. Как доказать на спичках, что если от 8 отнять 5, то ничего не останется?

1. Отнимите от 7 спичек 5 спичек так, чтобы и осталось тоже 5.

1. Положите 6 спичек так, как показано ниже:

_I_

VII

а) передвиньте одну спичку , не касаясь других, не трогая спичку, изображающую черту дроби, так, чтобы получилась дробь, равная 1.

б) превратите эту дробь в число 1/3, не изменяя количество данных спичек.

1. К разложенным на столе четырём спичкам прибавьте ещё пять спичек так, чтобы получилось сто.

I I I I

1. На рисунке из спичек образовано число 57 в римской нумерации.

LVII

Переместив две из них, не сдвигая остальных, получите 0. Предложите 2 способа.

1. Докажите, что половина 12 равна 7.

1. Увеличьте число, составленное из 10 спичек, в полтора раза, переложив как можно меньше спичек.

3. 

1. Передвиньте 1 спичку так, чтобы получилось правильное уравнение.
   II – I = II
   
   
   

2. Переложите 2 спички так, чтобы равенство было верным

X - VIII = III

1. Загадка – шутка.

Сын заспорил с отцом, что, если к пяти прибавить восемь, то можно получить один. И он спор выиграл. Как это у него получилось?

Глава 1. Геометрия на спичках

1. Шесть спичек.

Из шести спичек постройте 4 правильных треугольника

2. Переложите две спички из шестнадцати так, чтобы получилось 6 квадратов.

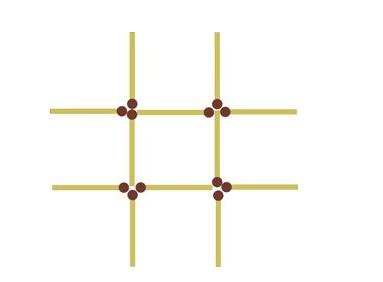
3. Переложите  в данной решетке 3 спички таким способом, чтобы образовалось три  квадрата.

4. Из спичек сложили  фигуру, похожую на   детскую игрушку  “неваляшку”.

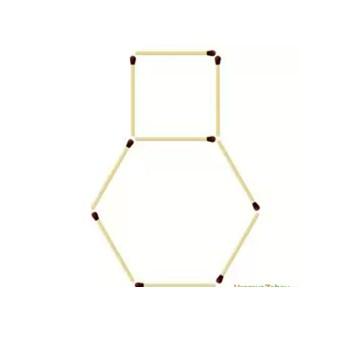
Вам необходимо  переложить три  спички, чтобы  эта неваляшка превратилась в куб.

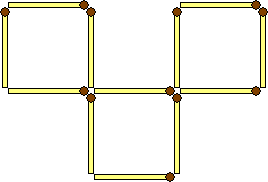
5. Переложите три спички из двенадцати так, чтобы получилось четыре одинаковых квадрата из трех.

6. Переложите три спички из двадцати четырех так, чтобы получилось 14 квадратов из

семи.

7. Переложите четыре спички из шестнадцати, чтобы получилось три квадрата

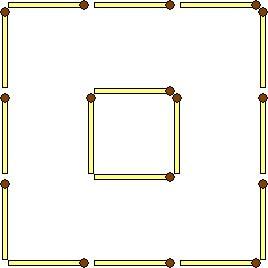
8. Переложить в фигуре, показанной на рисунке, пять спичек так, чтобы получилось три квадрата:

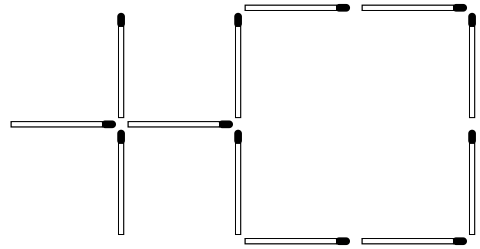
9. Из 9 спичек составить 6 квадратов.

10. Греческий храм. Этот храм построен из одиннадцати спичек. Требуется переложить четыре спички так, чтобы получилось пятнадцать квадратов

.

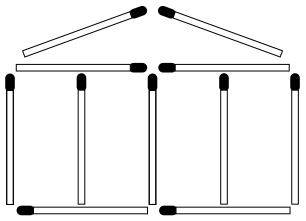
11. Фигура, изображённая на рисунке, составлена из восьми спичек, наложенных друг на друга. Снять 2 спички так, чтобы осталось 3 квадрата.

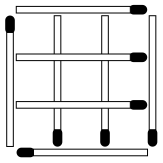
12. В изображённой на рисунке фигуре:

снять восемь спичек так, чтобы:

а) осталось только два квадрата;

б) осталось четыре равных квадрата;

в) переложите 12 спичек так, чтобы образовалось 2 равных квадрата;

г) уберите 3 спички так, чтобы осталось 7 равных квадратов;

д) уберите 4 спички так, чтобы оставшиеся образовали один большой и 4 маленьких квадрата;

е) уберите 4 спички так, чтобы оставшиеся образовали один большой и 3 маленьких квадрата;

ж) уберите 4 спички так, чтобы оставшиеся образовали 5 равных квадратов;

з) уберите 6 спичек так, чтобы оставшиеся образовали 5 равных квадратов;

и) уберите 8 спичек так, чтобы оставшиеся образовали 5 равных квадратов;

к) уберите 6 спичек так, чтобы получилось 2 квадрата и 2 равных неправильных шестиугольников;

л) уберите 6 спичек так, чтобы из оставшихся образовалось 3 квадрата;

м) уберите 8 спичек так, чтобы осталось 3 квадрата.

13. Спираль из спичек. Из 35 спичек выложена фигура, напоминающая «спираль». Переложите 4 спички так, чтобы образовалось 3 квадрата.

14. Данная равнобедренная трапеция составлена из десяти спичек.

Добавьте к ней еще пять таких  спичек, чтобы данная трапеция превратится в четыре равных трапеции.

 

15. Приложить к четырём спичкам пять спичек так, чтобы получилось сто:

Нужно найти два решения.

16. Из 12 спичек выложено 4 одинаковых квадрата. Переложите 2 спички, чтобы получилось 7 квадратов.

17. Из 12 спичек можно составить фигуру креста, площадь которого равна 5 «спичечным» квадратам:

Сложите из тех же 12 спичек одну связную фигуру так, чтобы её площадь равнялась 4 «спичечным» квадратам.

18. Из спичек сложена фигура, изображённая на рисунке. Переложите две спички так, чтобы получилось ровно четыре одинаковых квадрата с длиной стороны, равной длине спички?

19. Переложив четыре спички, превратите топор в три равных треугольника:

20. Переложите 6 спичек так, чтобы получилось 6 квадратов.

21. Уберите 17 спичек так, чтобы осталось 5 треугольников

22. Уберите 10 спичек так, чтобы образовалось 4 равных квадрата.

23. Восемнадцать спичек образовывают 6 одинаковых прилегающих друг к другу квадратов. Уберите 2 спички так, чтобы осталось 4 таких же квадрата.

24. Переложите 4 спички так, чтобы образовалось 10 квадратов.

25. Переложите 3 спички так, чтобы образовалось 3 равных квадрата.

26. В фигуре, представленной на рисунке, нужно так переложить 6 спичек с одного места на другое, чтобы образовалась фигура, составленная из 6 одинаковых четырехугольников.

27. В фигуре, составленной из 17 спичек, уберите 5 спичек, не перекладывая остальных, так, чтобы осталось всего 3 квадрата.

28. Из 12 спичек нужно составить фигуру, в которой было бы три одинаковых четырехугольника и два одинаковых треугольника. Как это сделать?

29. На этой головоломке передвиньте 1 спичку так, чтобы получилось 4 идентичных треугольника.

30. На рисунке изображен ключ.

а) Передвиньте 4 спички так, чтобы получилось три квадрата.
б) Передвиньте 3 спички, чтобы получить два прямоугольника.
в) Передвиньте 2 спички так, чтобы получилось два прямоугольника.

31. Из шести спичек, две из которых разломаны пополам, требуется составить 3 равных квадрата.

32. Есть 13 спичек по 5 см длиной каждая. Нужно ухитриться выложить из них метр.

Глава 1. Головоломки, разные задачи со спичками.

1. Спички разложены в три кучки по 11, 7 и 6 спичек.

Надо разложить их на 3 кучки, чтобы в каждой было по 8 спичек. Сделать это нужно за три хода, при этом добавлять можно только столько спичек, сколько уже есть в кучке.

1. Имеется две кучки спичек. В первой 7 спичек, во второй - 5. За один ход разрешается взять любое количество спичек, но из одной кучки. Проигрывает тот, кому нечего брать. Кто выигрывает при правильной игре - начинающий или его партнер? И как для этого ему надо играть?

1.  На столе лежат 37 спичек. Каждому из двух игроков разрешается по очереди брать не более 5 спичек. Выигрывает тот, кто возьмет последнюю. Кто выигрывает при правильной стратегии - начинающий игру или второй игрок? Какова выигрышная стратегия?

1. Из 18 спичек нужно сложить два четырехугольника так, чтобы площадь одного была больше площади другого. Спички, как и во всех предыдущих задачах, переламывать нельзя. Оба четырехугольника должны лежать обособленно, не примыкая друг к другу.

1. В «бокал», составленный из спичек, помещена вишня:

Необходимо, передвинув ровно две спички, переместить бокал так, чтобы вишня оказалась снаружи.

1. Из спичек построен дом. Переложить две спички так, чтобы дом повернулся другой стороной.

1. Весы составлены из девяти спичек и не находятся в состоянии равновесия. Переложите в них пять спичек так, чтобы весы оказались в равновесии.

1. На рисунке вы видите корову, у которой есть все, что полагается: голова, туловище, ноги, рога и хвост. Корова на рисунке смотрит влево. 
   Переложите ровно две спички так, чтобы она смотрела вправо.

1. Расположите 6 спичек так, чтобы каждая спичка соприкасалась с остальными пятью.
   

2. На рисунке показана крепость и каменная стена вокруг нее. Между крепостью и стеной находится ров, наполненный водой, с голодными крокодилами в ней. Показать, как с помощью двух спичек можно проложить мост между крепостью и стеной.

1. На рисунке с помощью 15,5 спичек выложена грустная свинья.

а) Сделайте ее веселой, переложив 3,5 спички.

б) Сделайте свинью любопытной, убрав одну спичку и, переложив   2,5 спички.

1. Спичечный рак ползёт вверх. Переложить три спички так, чтобы он пополз вниз.

1. Переложите 3 спички, чтобы стрела поменяла своё направление на противоположное.

1. На этой картинке 6 маленьких секций для кроликов. Можете ли вы построить 6 клеток для кроликов, используя только 12 спичек?

Ответы.

Глава 1. Числа и цифр

1. X - VI = IV или XI - V = VI или XI - VI = V 

1. VI = IX - III или VI = IV + II
   
   
   

2. XV + V = XX
   
   
   

3. IX - IV = V
   
   
   

4. X - VIII = II

1. Корень квадратный из 1

1. C - L = L или L + I = LI

1. V + IV = IX или VI + IV = X

2. VI + V =XI

3. VII + V = XII

4. X - IX = I

5. X - IV = VI

6. VIII + IX = XVII

7. IX - корень из единицы = X

8. VII = IX - II

9. X + корень из единицы XI

10. X = II + VIII

11. I + I = X- I

12. I+I = II

13. IX + I = X

14. II=II

15. I + I = II

16. III- II = I

17. II = II = II

18. VI = V + I

19. II = IIII - II

20. III - I = I + I

21. XI - V = VI

22. VIII - III = V или VII + III= X или VII – III= IV

23. VI + III = IX

24. XIII - VII = VI

25. VIII + IX = XVII

26. IX + I = X

27. 5 + 5 +5 = 550 (545 +5= 550)

28. VII = X-III

29. XII : III = IV

: : :

VI : III = II

= = =

II : I = II

1. В каждом из трех горизонтальных рядов переложите по одной спичке так, чтобы шесть равенств (вертикальных и горизонтальных) оказались верными

IV ∙ II = VIII

∙ ∙ ∙

I ∙ IV = IV

= = =

I V ∙ VIII = XXXII

39. а) квадратный корень из единицы

б) V

I

1. VI или

I

1. VIII

1. Изобразим число VIII. От VIII отнять 5 спичек и ничего не останется

1. Семью спичками изобразим число XXVI . Заберем 5 спичек и оставим V.

1. Положите 6 спичек так, как показано ниже:

а) _I_ б) II

V I VI

Или

1. I – V I или V I - I

1. XII

48.

49. I + I = II или II + = II

50. IX - VIII = II

51. С помощью пяти и восьми спичек он выложил слово «один».

Глава 2. Геометрия на спичках

1. Шесть спичек.

Надо построить правильную треугольную пирамиду.

2. Переложите две спички из шестнадцати так, чтобы получилось 6 квадратов.

3. Переложите  в данной решетке 3 спички таким способом, чтобы образовалось три  квадрата.

4. Ответ.

5. Переложите три спички из двенадцати так, чтобы получилось четыре одинаковых квадрата из трех.

Ответ

6. Переложите три спички из двадцати четырех так, чтобы получилось 14 квадратов из

семи. Ответ

7. Переложите четыре спички из шестнадцати, чтобы получилось три квадрата

Ответ

8. Переложить в фигуре, показанной на рисунке, пять спичек так, чтобы получилось три квадрата:

9. Из 9 спичек составить 6 квадратов.

10. Греческий храм. Этот храм построен из одиннадцати спичек. Требуется переложить четыре спички так, чтобы получилось пятнадцать квадратов

.

11. Фигура, изображённая на рисунке, составлена из восьми спичек, наложенных друг на друга. Снять 2 спички так, чтобы осталось 3 квадрата.

Ответ

12. В изображённой на рисунке фигуре:

уберите восемь спичек так, чтобы:

а) осталось только два квадрата;

б) осталось четыре равных квадрата;

Вариант 1

Вариант 2

в) переложите 12 спичек так, чтобы образовалось 2 равных квадрата;

г)

д) уберите 4 спички так, чтобы оставшиеся образовали один большой и 4 маленьких квадрата;

е) уберите 4 спички так, чтобы оставшиеся образовали один большой и 3 маленьких квадрата;

ж) уберите 4 спички так, чтобы оставшиеся образовали 5 равных квадратов;

з) уберите 6 спичек так, чтобы оставшиеся образовали 5 равных квадратов;

и) уберите 8 спичек так, чтобы оставшиеся образовали 5 равных квадратов;

к)

л) уберите 6 спичек так, чтобы из оставшихся образовалось 3 квадрата;

м) уберите 8 спичек так, чтобы осталось 3 квадрата.

13. Спираль из спичек. Из 35 спичек выложена фигура, напоминающая «спираль». Переложите 4 спички так, чтобы образовалось 3 квадрата.

14. Ответ

15.

Первое решение:

Второе решение:

16. Из 12 спичек выложено 4 одинаковых квадрата. Переложите 2 спички так, чтобы получилось 7 квадратов.

17. Чтобы убедиться, что площадь этой фигуры равна 4, дополним мысленно её до треугольника:

Согласно теореме Пифагора, этот треугольник является прямоугольным (квадрат длины его гипотенузы — 5² — равен сумме квадратов длин его катетов — 3² + 4²). Значит, его площадь равна половине произведения длин его катетов, то есть 6 «спичечным» квадратам. А так как площадь заштрихованной области равна 2 «спичечным» квадратам, то площадь построенной нами фигуры равна в точности 4 «спичечным» квадратам.

18.

19. Топор.

20. Переложите 6 спичек так, чтобы получилось 6 квадратов. Ответ:

21. Уберите 17 спичек так, чтобы осталось 5 треугольников

22. Уберите 10 спичек так, чтобы образовалось 4 равных квадрата.

1 вариант 2 вариант.

3 вариант. 4 вариант

23.

24. Переложите 4 спички так, чтобы образовалось 10 квадратов.

25. Переложите 3 спички так, чтобы образовалось 3 равных квадрата.

26. В фигуре, представленной на рисунке, нужно так переложить 6 спичек с одного места на другое, чтобы образовалась фигура, составленная из 6 одинаковых четырехугольников.

27. В фигуре, составленной из 17 спичек, уберите 5 спичек, не перекладывая остальных, так, чтобы осталось всего 3 квадрата.

28. Из 12 спичек нужно составить фигуру, в которой было бы три одинаковых четырехугольника и два одинаковых треугольника. Как это сделать?

29. На этой головоломке передвиньте 1 спичку так, чтобы получилось 4 идентичных треугольника.

Ответ.

30. На рисунке изображен ключ.

а) Передвиньте 4 спички так, чтобы получилось три квадрата.

б) Передвиньте 3 спички, чтобы получить два прямоугольника.

в) Передвиньте 2 спички так, чтобы получилось два прямоугольника.

31. Из шести спичек, две из которых разломаны пополам, требуется составить 3 равных квадрата.

32. Есть 13 спичек по 5 см длиной каждая. Нужно ухитриться выложить из них метр.

Глава 3. Головоломки, разные задачи со спичками.

1. 4  14   6

4   8   12

1.   8    8

2. При правильной игре выигрывает начинающий игрок. Его стратегия: первым ходом он должен сравнять количество спичек в кучках, т.е. взять из первой кучки 2 спички. Каждый следующий его ход должен быть "симметричен" ходу второго игрока, т.е. если "второй" берет n спичек из одной кучки, то "первый" должен взять также n спичек, но из другой кучки. Таким образом, если может сделать ход "второй" игрок, то может сделать ход и "первый". Так как после каждого хода количество спичек уменьшается, то наступит момент, когда "второй" не сможет сделать ход (ни в одной из кучек спичек не останется) и проиграет.

3.  Начинающий первым ходом берет одну спичку, а затем каждый раз дополняет число спичек, взятых соперником, до шести.

4. Площадь верхней фигуры образуют два квадрата, каждый со сторонами в одну спичку. Нижний четырехугольник представляет собой параллелограмм, высота которого AB = 1.5 спички. Площадь параллелограмма по правилам геометрии равна его основанию, умноженному на высоту: 4*1.5 = 6, т.е. втрое больше площади верхнего четырехугольника.

1. Вишня.

7.

8. Задача с коровой.

9.

10. Крепость.

11. Задача о свинье.

12. Спичечный рак

13.

14.

Использованная литература.

1. Кротов И.С. Гимнастика для ума.-Москва: ЗАО «БАО-ПРЕСС», ООО «ИД «РИПОЛ классик», 2005 г.

2. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 классов ср.шк.-5-е издание.-М.: Просвещение, 1988.-160 с.

3. Коваленко В.Г. Дидактические игры на уроках математики: Кн. Для учителя.-М.-Просвещение, 1990.

4. Никольская И.Л. Гимнастика для ума: книга для учащихся начальных классов,- М.: Издательство «Экзамен», 2013

5. Савин А.П. Занимательные математические задачи.- М.: АСТ, 1995.

6. Трошин В.В. Занимательные задачи, упражнения и игры со спичками в средней школе на уроках и на внеклассных занятиях.-Волгоград: Учитель, 2008.