Сборник заданий по математике для Городской Ломоносовской олимпиады
1.Решите в целых числах уравнение: y-x-xy2;
2.Вычислите: _____1____ ____1_____
7-24 + 1 7 + 24 – 1
3.Найти сумму целых отрицательных корней уравнения: |X+2|X+2
4. При каких значениях параметра «a» уравнение имеет ровно один корень : (x-a)x50
5. Простым или составным является число 49 + 610+320 ?(ответ пояснить)
6. Решите уравнение 2 Sin2 х = 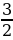 + Sin x ∙ Sin 3x
+ Sin x ∙ Sin 3x
7. Сумма первых десяти членов арифметической прогрессии равна 30. Четвертый, седьмой и пятый члены этой прогрессии, взятые в указанном порядке, представляют собой три последовательных члена геометрической прогрессии. Найти разность арифметической прогрессии.
8. Вычислите Cos 70 ( Cos2 20 – 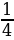 )
)
9. Решите уравнение
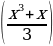 +
+ 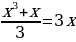
10.Решите уравнение
 (
(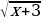 – х +3)
– х +3)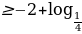
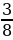
11. Диагональ BD вписанного четырехугольника ABCD является биссектрисой угла ABC. Найдите площадь этого четырехугольника, если BD = 6 см., угол ABC = 60 .
12.Решите неравенство (0,05) 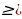
13. Найдите все положительные решения системы уравнений.
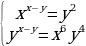
14. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке K. Найти длину отрезка KC, если BC=4, а AK=6.
15. Найдите все целочисленные пары (x; y), удовлетворяющие уравнению
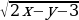 +
+ 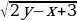 = 2
= 2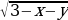
16. Дан треугольник АВС, в котором угол В равен 30 градусов, АВ= 4 и ВС= 6.Биссектриса угла В пересекает сторону АС в точке Д. Определите площадь треугольника АВД.
17. Решите уравнение 2cos2x = 8cosx + 3.
18. Треугольник АВС – равнобедренный, угол ВАС равен 120 градусов. На продолжении стороны АС за вершину А взята точка Д так, что АД= 2АВ. Докажите, что треугольник ВДС также равнобедренный.
19. Единица измерения скорости на море.
20. Кто автор первого российского учебника математики?
21. Чему равен один пуд?
22. Какой русский писатель окончил физико-математический факультет?
23. Другое название двучлена.
24. В каком треугольнике один и тот же отрезок выполняет тройную нагрузку?
25. Стороны треугольника равны 3, 4 и 5 единицам. Определите вид треугольника в зависимости от углов. Как называется такой треугольник?
26. Как называется функция, графиком которой является прямая?
27. Какой знак имеет sin 3 ?
28. Ученый, который известен как создатель школы математиков. Он открыл замечательное свойство прямоугольных треугольников.
29.Через середину М стороны ВС параллелограмма АВСД, площадь которого равна 1, и вершину А проведена прямая, пересекающая диагональ ВД в точке О. Найдите площадь четырехугольника ОМСД.
Найдите сумму корней уравнения (х-3)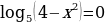 .
.
Решите уравнение 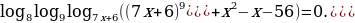
Без чего не могут обойтись охотники, барабанщики и математики?
Как называется знак корня?
Угол, соответствующий дуге, длина которой равна радиусу.
Математик, именем которого названа теорема, выражающая связь между координатами квадратного уравнения.
Другое название многочлена.
Утверждение, принимаемое без доказательства.
Как по-другому называется миллиард?
Раздел математики, изучающий числа и простейшие действия над ними.
Человек, который хотел быть и юристом, и философом, но стал математиком. Он первым ввел в математику прямоугольную систему координат.
Как называется третья координата точки в пространстве?
Решите систему уравнений
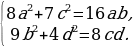
43.Найдите все значения a, при каждом из которых уравнение
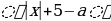 = 2 имеет ровно 3 корня.
= 2 имеет ровно 3 корня.
44.Правильный треугольник ABC со стороной, равный 3, вписан в окружность. Точка D лежит не в окружности, причем длина хорды AD равна 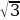 . Найти длины хорд BD и CD.
. Найти длины хорд BD и CD.
45. Получите 100, используя тринадцать троек и арифметические действия.
46.Найдите наименьшее значение а, при котором сумма квадратов корней уравнения 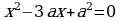 равна 0,28.
равна 0,28.
47. Какая из сумм больше и на сколько:
S(sin)=sin1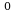 + sin2
+ sin2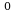 +sin3
+sin3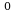 +…+sin90
+…+sin90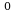 или S(cos)= cos 1
или S(cos)= cos 1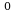 +cos2
+cos2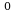 + cos3
+ cos3 +…+cos90
+…+cos90 ?
?
48.Решите уравнение 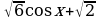 │sinx│=2.
│sinx│=2.
49.Найдите радиус окружности, описанной около равнобедренного треугольника с основанием 6, если синус одного его угла равен косинусу другого.
50. Трапеция АВСД с основанием АД=6 вписана в окружность. Касательная к окружности в точке А пересекает прямые ВД и СД в точках М и N соответственно. Найдите AN, если AB МД и АМ=3.
МД и АМ=3.
51.Чему равна разность произведений?
201120112011 201120112011 - 201120112010
201120112011 - 201120112010 201120112012
201120112012
52.На покраску дома желтой краски потребовалось больше, чем белой на 20%, а коричневой краски на 25% меньше, чем желтой. На сколько процентов коричневой и желтой краски суммарно потребовалось больше, чем белой?
53.При каких значениях a существует единственное решение системы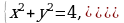
54.Две окружности касаются друг друга внутренним образом в точке К. Хорда АВ большей окружности касается меньшей окружности в точке L, причем AL =10. НайдитеBL,если AK:BK=2:5.
55.Можно лииз квадрата со стороной 3 вырезать многоугольник площади 6, которым можно полностью без наложений и пустот обернуть единичный куб?
56.Решите неравенство

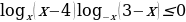
57. Образно представьте себе нашу планету, плотно стянутую кольцом по всему ее экватору. После увеличения длины окружности кольца на 10 метров, между кольцом и поверхностью земли образовался зазор определенной величины. Как Вы считаете, сможет ли человек пройти, или хотя бы протиснуться в этот зазор? Известно, что экватор имеет длину приблизительно равную 40 075 километров.
58. Назовите два числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел.
59. Решить уравнение 
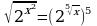 .
.
60. Решить уравнение
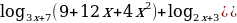
61. На основании AC равнобедренного треугольника ABC взята точка E, а на боковых сторонах AB и BC точки D и F соответственно так, что DE∥BC и EF∥AB. Какую часть площади треугольника ABC занимает площадь треугольника DEF, если BF:EF=2:3?
62. В наклонной треугольной призме длины боковых ребер равны 8 см. Стороны перпендикулярного сечения относятся как 9:10:17, а его площадь равна 144 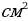 . Определите площадь боковой поверхности призмы.
. Определите площадь боковой поверхности призмы.
63.Трехзначное число состоит из возрастающих (слева направо) цифр. Если это число прочитать, то все слова будут начинаться на одну и ту же букву. Что это за число?
64.В прямоугольном треугольнике с катетом 2 и гипотенузой 4 найдите угол между высотой и биссектрисой, проведёнными из прямого угла. Ответ укажите в градусах.
65.Возвращаясь с рыбалки домой, рыболов встретил своего приятеля, который поинтересовался его уловом. Но, так как наш рыболов помимо рыбалки был также большим любителем всякого рода загадок, ответил приятелю следующим образом: “Если к количеству пойманной мною рыбы добавить половину улова и еще десяток рыбин, то мой улов составил бы ровно сотню рыб”. Сколько рыбы поймал рыболов?
66. Найдите сумму квадратов корней уравнения
2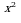

 = 4
= 4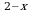
67. Две окружности касаются друг друга внутренним образом в точке K. Хорда AB большей окружности касается меньшей окружности в точке L, причем AL = 10.Найдите BL, если AK : BK = 2 : 5. 68. Найдите все корни уравнения sin(πcos2x)+cos(πcos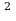 x)=0, принадлежащие интервалу (−7π/6;−π/3). В ответ запишите делённую на π сумму этих корней (в радианах), округлив её при необходимости до двух знаков после запятой.
x)=0, принадлежащие интервалу (−7π/6;−π/3). В ответ запишите делённую на π сумму этих корней (в радианах), округлив её при необходимости до двух знаков после запятой.
69. Четырехугольник АВСД вписан в окружность. Диагональ АС является биссектрисой угла ВАД и пересекается с диагональю ВД в точке К. Найдите КС, если ВС=4, а АК=6.
В шахматном турнире каждый шахматист сыграл с каждым по одному разу и каждый шахматист все партии, кроме одной, завершил вничью. Сколько шахматистов участвовало в турнире, если всего было зафиксировано 264 ничьи?
71. Вычислите arctg 1+arctg 2+arctg 3. 72. Квадрат АВСД вписан в окружность. Хорда СЕ пересекает диагональ ВД в точке К.
а) Докажите, что произведение СК*СЕ равно площади квадрата.
б) Найдите отношение СК: КЕ, если угол ЕСД равен 15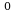 .
.
73.В треугольнике АВС проведена высота ВД (точка Д лежит на стороне АС). Оказалось, что АВ=2СД и СВ=2АД. Найдите углы треугольника АВС.
74.Решите неравенство
7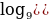 ≤8+
≤8+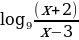
75. Какое число больше: 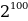 или
или 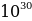 ?
?
76. Функция f(x) имеет вид f (х) = 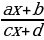 , где a,b,c,d- некоторые числа. Известно, что f(0)=1, f(1)=0, f(2)=3. Чему равно значение f(3) ?
, где a,b,c,d- некоторые числа. Известно, что f(0)=1, f(1)=0, f(2)=3. Чему равно значение f(3) ?
77. Найти углы прямоугольного треугольника, в котором гипотенуза вчетверо длиннее высоты, на нее опущенной.
78. Основание АВ трапеции АВСД вдвое больше основания СД , а ее диагонали пересекаются в точке О. Какую часть площади трапеции составляет площадь треугольника СОД?
79. Цена бриллианта пропорциональна квадрату его веса. Бриллиант весом 24 карата был разбит на две части, отчего его стоимость уменьшилась в 1,6 раза. Найти вес частей, на которые он был разбит.
80. Решите неравенство 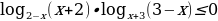 .
.
81. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?
82. Найдите значение выражения 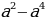 , если
, если 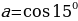 .
.
83. Известно tg α+tg β=2, ctg α +ctg β =3. Вычислите tg (α+β).
84. Решите уравнение 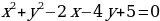 .
.
85. Каков радиус окружности, описанной около равнобедренного треугольника с основанием 6 и высотой 1?
86.Постройте график функции y=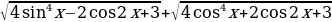 .
.
87. Общая касательная двух пересекающихся окружностей касается их в точках А и В. В каком отношении прямая, проходящая через точки пересечения окружностей, разделит отрезок АВ?
88. На плоскости дан отрезок АВ. Где может быть расположена точка С, чтобы треугольник АВС был остроугольным?







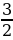 + Sin x ∙ Sin 3x
+ Sin x ∙ Sin 3x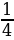 )
)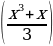 +
+ 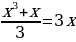
 (
(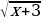 – х +3)
– х +3)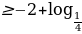
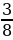
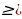
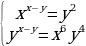
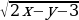 +
+ 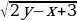 = 2
= 2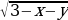
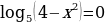 .
. 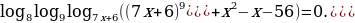
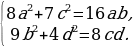
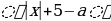 = 2 имеет ровно 3 корня.
= 2 имеет ровно 3 корня.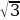 . Найти длины хорд BD и CD.
. Найти длины хорд BD и CD.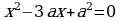 равна 0,28.
равна 0,28.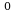 + sin2
+ sin2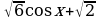 │sinx│=2.
│sinx│=2. МД и АМ=3.
МД и АМ=3.
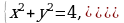
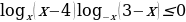
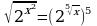 .
. 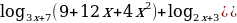
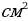 . Определите площадь боковой поверхности призмы.
. Определите площадь боковой поверхности призмы. 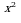
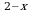
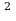 x)=0, принадлежащие интервалу (−7π/6;−π/3). В ответ запишите делённую на π сумму этих корней (в радианах), округлив её при необходимости до двух знаков после запятой.
x)=0, принадлежащие интервалу (−7π/6;−π/3). В ответ запишите делённую на π сумму этих корней (в радианах), округлив её при необходимости до двух знаков после запятой.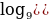 ≤8+
≤8+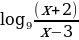
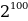 или
или 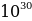 ?
?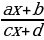 , где a,b,c,d- некоторые числа. Известно, что f(0)=1, f(1)=0, f(2)=3. Чему равно значение f(3) ?
, где a,b,c,d- некоторые числа. Известно, что f(0)=1, f(1)=0, f(2)=3. Чему равно значение f(3) ?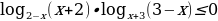 .
.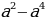 , если
, если 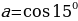 .
. 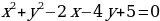 .
. 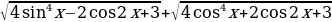 .
.









