2016-2017
ОЛИМПИАДА

УЧИТЕЛЬ Адильханова О.А.
 Учащийся_________________________________________________
Учащийся_________________________________________________
1. Каждое ребро куба покрашено в красный или чёрный цвет. При этом каждая грань куба имеет хотя бы одно чёрное ребро. Какое наименьшее количество рёбер могло быть покрашено в чёрный цвет?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
2. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
(A) 18 часов (B) 6 часов (C) 9 часов (D) 15 часов (E) 21 час
3. Пусть выражение a ¤ b обозначает сумму цифр в произведении a ? b. Тогда (15 ¤ 10) ¤ (15 ? 10) =
(A) 5 (В) 6 (С) 9 (D) 10 (Е) 150
4. На плоскости через данную точку провели 8 прямых линий. Какое наибольшее число прямых углов могло при этом образоваться?
(A) 4 (В) 8 (С) 12 (D) 16 (Е) 20
5. В одной комнате сидят 9 человек, и их средний возраст - 25 лет. В другой комнате сидят 11 человек, и их средний возраст - 45 лет. Каков средний возраст всех 20 человек?
(A) 40 (В) 36 (С) 35 (D) 32 (Е) 30
6. 12 мальчиков и 8 девочек являются членами математического клуба. Каждую неделю в клуб принимают двух новых девочек и одного мальчика. Сколько будет членов в клубе в тот день, когда мальчиков и девочек станет поровну?
(A) 20 (B) 24 (C) 28 (D) 32 (E) 36
7. Улитка взбирается на ветку длиной 10 дм. За день она поднимается на 4 дм, а за ночь сползает вниз на 3 дм. Через сколько дней улитка достигнет конца ветки?
(A) 7 (В) 8 (С) 9 (D) 10 (Е) 11
8. Белоснежка раздавала семи гномам грибы. Каждый следующий гном получал на один гриб больше предыдущего, а все вместе они получили 707 грибов. Сколько грибов получил последний гном?
(A) 98 (В) 100 (С) 101 (D) 104 (Е) 107
9. Человек говорит: . Сколько ему полных лет?
(A) 44 (В) 47 (С) 48 (D) 49 (Е) 50
10. Сколько прямоугольных пластин 20 ? 45 см можно вырезать из фанерного листа 120 ? 240 см?
(A) 29 (В) 30 (С) 31 (D) 32 (Е) 33
11. Чтобы пронумеровать страницы книги с первой по последнюю, потребовалась 4221 цифра. Сколько страниц в этой книге?
(A) 1108 (В) 1246 (С) 1332 (D) 1533 (Е) 1665
12. Ребро куба равно 1. Муха ползает по рёбрам этого куба, не проходя по одному ребру дважды (но, возможно, проходя несколько раз через одну вершину). Какой самый длинный путь она может проползти?
(A) 6 (B) 8 (C) 9 (D) 10 (E) 12
13. Четыре футбольные команды сыграли круговой турнир. За победу начисляется 3 очка, за ничью 1 очко. Команды набрали 5, 3, 3 и 2 очка. Сколько было ничьих?
(A) 5 (В) 4 (С) 3 (D) 2 (Е) 1
14. Джон может купить бутылку сока за 3 доллара. Пустую бутылку можно сдать за 2 доллара. Сколько бутылок сока может выпить Джон, имея 10 долларов?
(A) 3 (B) 5 (C) 6 (D) 8 (E) 9
Ответы:
1.B 2.C 3.C 4.D 5.B 6.D 7.A 8.D 9.C 10.C 11.C 12.C 13.A 14.D
 9 класс
9 класс
Задача 1. Найдите значение выражения (1+ )(1+
)(1+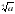 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )(1–
)(1– ) при а=2003.
) при а=2003.
Решение.
Применяя формулу ( х – у )( х + у ) = х² – у² последовательно для последних двух множителей, в результате получим: (1- )(1+
)(1+ ) = 1 - a.
) = 1 - a.
При а = 2003 получим 1– а = 1 – 2003 = – 2002.
Ответ: – 2002.
Задача 2.При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
Решение. Пусть  – общий корень данных трехчленов, тогда
– общий корень данных трехчленов, тогда
 +a
+a +1= 0 и
+1= 0 и  +
+ + а = 0, т.е.
+ а = 0, т.е.
 +a
+a +1=
+1= +
+ +а
+а  a
a +1=
+1= + а
+ а а(
а( –1)=
–1)=  –1
–1 (
( – 1)( а – 1)=0.
– 1)( а – 1)=0.
Тогда а = 1 или  =1.
=1.
Если а = 1, то трехчлены оба имеют вид х²+х+1 и не имеют действительных корней.
Если  =1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а = – 2.
=1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а = – 2.
Ответ: а = – 2.
Задача 3. Сколько цифр содержит число  ?
?
Решение.  =(
=( )
) =
= =1 250 000 000 000.
=1 250 000 000 000.
Задача 4. Делится ли число 102002 + 8 на 9?
Решение. Первая цифра этого числа – 1 , последняя цифра – 8, а между ними 2001 раз повторяется цифра 0. Сумма цифр равна 9. Значит, число делится на 9. Ответ: Да.
Задача 4. Построить график функции, заданной формулой  .
.
Решение. Упростим 

Тогда график будет состоять из линий:

 9 класс
9 класс
Задача 1. Найдите значение выражения (1+ )(1+
)(1+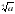 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )(1–
)(1– ) при а=2003.
) при а=2003.
Задача 2.При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
Задача 3. Сколько цифр содержит число  ?
?
Задача 4. Делится ли число 102002 + 8 на 9?
Задача 5. Построить график функции, заданной формулой  .
.
 9 класс
9 класс
Задача 1. Найдите значение выражения (1+ )(1+
)(1+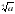 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )(1–
)(1– ) при а=2003.
) при а=2003.
Задача 2.При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
Задача 3. Сколько цифр содержит число  ?
?
Задача 4. Делится ли число 102002 + 8 на 9?
Задача 5. Построить график функции, заданной формулой  .
.
 9 класс
9 класс
Задача 1. Найдите значение выражения (1+ )(1+
)(1+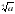 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )(1–
)(1– ) при а=2003.
) при а=2003.
Задача 2.При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
Задача 3. Сколько цифр содержит число  ?
?
Задача 4. Делится ли число 102002 + 8 на 9?
Задача 5. Построить график функции, заданной формулой 
11 класс
Задача 1.
Решить систему уравнений 
Решение. 
Замена: Пусть  , тогда
, тогда  . Решая уравнение относительно u, получим 6u2 – 13u + 6 = 0.
. Решая уравнение относительно u, получим 6u2 – 13u + 6 = 0.
Откуда 
Возвращаемся к замен
Но уравнение у 2 = – 1 не имеет решения
Ответ: ( 5; 1 ), ( - 5; - 1 ).
Задача 2.
Площадь треугольника ABC равна 2. Найдите площадь сечения пирамиды ABCD плоскостью, проходящей через середины ребер AD, BD, CD.
Решение.
В сечении получится ∆ KLM, стороны которого - средние линии
треугольников ADB, BDC и ADC. Значит ∆KLM ~∆ABC, где  .
.
Значит  = S∆ KLM = S∆ АВС ∙ k2
= S∆ KLM = S∆ АВС ∙ k2
S∆ KLM = 2 ∙  =
= 
Ответ: 
Задача 3.
Дан график функции у = х2 + ах + а. Найдите значение а.
Решение. Данный трехчлен имеет 1 корень, значит D = 0.
D = а2 – 4а

Если а = 0, то уравнение принимает вид у = х2 и графиком функции является парабола с вершиной в начале координат. Значит а = 0 не является решением задачи.
Ответ: а = 4.
Задача 4. Построить график функции: у = +
+
Решение.
y= +
+
y= +
+
y=  +
+
y= 2sin²x+1+2cos²x+1
y=4
Значит, графиком функции является прямая, заданная уравнением у=4.
Задача 5. В треугольнике ABC величина угла А вдвое больше величины угла В, а длины сторон, противолежащих этим углам, равны соответственно 12 см и 8 см. Найти длину третьей стороны треугольника.

Решение.
Пусть АК –биссектриса угла А.
 ~
~

 (см).
(см).
Ответ: 10 .
2.Учащийся___________________________
1. Каждое ребро куба покрашено в красный или чёрный цвет. При этом каждая грань куба имеет хотя бы одно чёрное ребро. Какое наименьшее количество рёбер могло быть покрашено в чёрный цвет?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
2. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
(A) 18 часов (B) 6 часов (C) 9 часов (D) 15 часов (E) 21 час
3. Пусть выражение a ¤ b обозначает сумму цифр в произведении a ? b. Тогда (15 ¤ 10) ¤ (15 ? 10) =
(A) 5 (В) 6 (С) 9 (D) 10 (Е) 150
4. На плоскости через данную точку провели 8 прямых линий. Какое наибольшее число прямых углов могло при этом образоваться?
(A) 4 (В) 8 (С) 12 (D) 16 (Е) 20
5. В одной комнате сидят 9 человек, и их средний возраст - 25 лет. В другой комнате сидят 11 человек, и их средний возраст - 45 лет. Каков средний возраст всех 20 человек?
(A) 40 (В) 36 (С) 35 (D) 32 (Е) 30
6. 12 мальчиков и 8 девочек являются членами математического клуба. Каждую неделю в клуб принимают двух новых девочек и одного мальчика. Сколько будет членов в клубе в тот день, когда мальчиков и девочек станет поровну?
(A) 20 (B) 24 (C) 28 (D) 32 (E) 36
7. Улитка взбирается на ветку длиной 10 дм. За день она поднимается на 4 дм, а за ночь сползает вниз на 3 дм. Через сколько дней улитка достигнет конца ветки?
(A) 7 (В) 8 (С) 9 (D) 10 (Е) 11
8. Белоснежка раздавала семи гномам грибы. Каждый следующий гном получал на один гриб больше предыдущего, а все вместе они получили 707 грибов. Сколько грибов получил последний гном?
(A) 98 (В) 100 (С) 101 (D) 104 (Е) 107
9. Человек говорит: . Сколько ему полных лет?
(A) 44 (В) 47 (С) 48 (D) 49 (Е) 50
10. Сколько прямоугольных пластин 20 ? 45 см можно вырезать из фанерного листа 120 ? 240 см?
(A) 29 (В) 30 (С) 31 (D) 32 (Е) 33
11. Чтобы пронумеровать страницы книги с первой по последнюю, потребовалась 4221 цифра. Сколько страниц в этой книге?
(A) 1108 (В) 1246 (С) 1332 (D) 1533 (Е) 1665
12. Ребро куба равно 1. Муха ползает по рёбрам этого куба, не проходя по одному ребру дважды (но, возможно, проходя несколько раз через одну вершину). Какой самый длинный путь она может проползти?
(A) 6 (B) 8 (C) 9 (D) 10 (E) 12
13. Четыре футбольные команды сыграли круговой турнир. За победу начисляется 3 очка, за ничью 1 очко. Команды набрали 5, 3, 3 и 2 очка. Сколько было ничьих?
(A) 5 (В) 4 (С) 3 (D) 2 (Е) 1
14. Джон может купить бутылку сока за 3 доллара. Пустую бутылку можно сдать за 2 доллара. Сколько бутылок сока может выпить Джон, имея 10 долларов?
(A) 3 (B) 5 (C) 6 (D) 8 (E) 9






 Учащийся_________________________________________________
Учащийся_________________________________________________  9 класс
9 класс )(1+
)(1+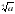 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )(1–
)(1– – общий корень данных трехчленов, тогда
– общий корень данных трехчленов, тогда +a
+a a
a









