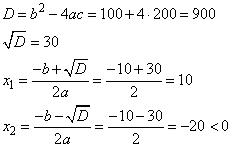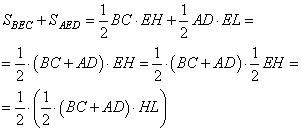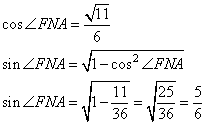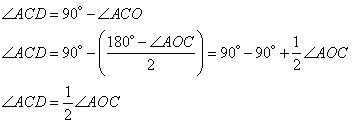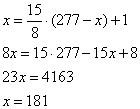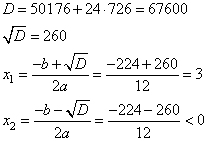| В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что прямые АВ и CF параллельны. Найдите CF, если FK = 4√3. Так как ABCD – равнобедренная трапеция, то 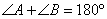 и и 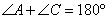 . Учитывая, что AK и CF1 – биссектрисы, то . Учитывая, что AK и CF1 – биссектрисы, то 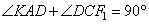 . По условию задания . По условию задания 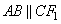 , следовательно, , следовательно, 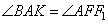 как накрест лежащие. Углы как накрест лежащие. Углы 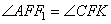 как вертикальные, следовательно, как вертикальные, следовательно,  . Получаем прямоугольный треугольник CFK с гипотенузой CF. . Получаем прямоугольный треугольник CFK с гипотенузой CF. 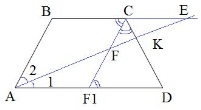
Точка E лежит на пересечении прямых AK и BC, углы 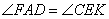 , следовательно, треугольник CFE – равнобедренный (CF=CE) с высотой CK. Значит, CK также и биссектриса, получаем: , следовательно, треугольник CFE – равнобедренный (CF=CE) с высотой CK. Значит, CK также и биссектриса, получаем: 
Рассмотрим прямоугольный треугольник FCK с углом C=60º и стороной FK=4√3. 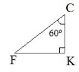
Для него справедливо отношение: 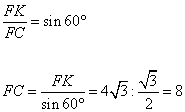
Ответ: 8 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18. 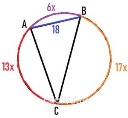 Длины дуг относятся как 6:13:17. Пусть ‿АВ = 6х, ‿АС = 13х, ‿ВС =17х. Вся окружность равна 360°. Найдём ‿АВ: ‿АВ + ‿АС + ‿ВС = 360º
6х + 13х + 17х = 360
36х = 360
х = 360/36 = 10
‿АВ = 6х = 6·10 = 60º Вписанный угол (∠С) всегда в два раза меньше дуги на которую опирается: ∠С = ‿АВ/2 = 60/2 = 30º По теореме синусов найдём радиус (R) окружности: 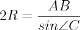
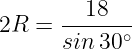
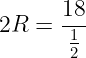
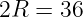
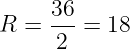
Ответ: 18. Прямая пересекает стороны АВ и ВС треугольника ABC в точках K и N соответственно. Известно, что АВ = 12, ВС = 15, АС = 24, AK = 7, CN = 11. Найдите длину отрезка KN. Решение. В треугольнике KBN: KB = 12-7 = 5, BN = 15-11 = 4. В треугольниках ABC и NBK угол В общий и 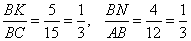
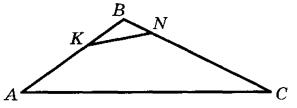
Следовательно, треугольники ABC и NBK подобны. Значит, 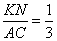
откуда 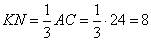
Ответ: 8. В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что угол AFC равен 150°. Найдите FK, если CF = 12√3. Основания трапеции ABCD параллельны друг другу (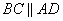 ), следовательно, ), следовательно, 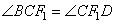 (как накрест лежащие). Также в трапеции (как накрест лежащие). Также в трапеции 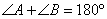 , значит, , значит, 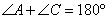 . Получаем, что . Получаем, что 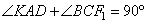 . Так как AK и CF1 – биссектрисы, то . Так как AK и CF1 – биссектрисы, то 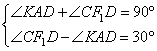
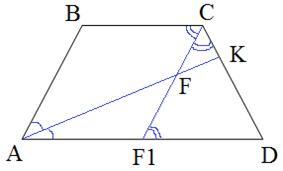
Решаем систему, имеем: 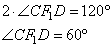
По условию угол AFC=150º, значит, угол CFK=30º, следовательно, 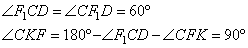
Получаем прямоугольный треугольник CFK с гипотенузой CF. Так как CF=12√3, то 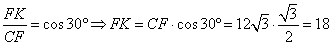
Ответ: 18
Точка K — середина боковой стороны CD трапеции ABCD. Докажите, что площадь треугольника KAB равна половине площади трапеции. Продолжим BK до пересечения с прямой AD в точке F. Заметим, что в треугольниках FDK и BCK стороны CK и DK равны по условию, углы при вершине K равны как вертикальные, а углы KDF и KCB равны как накрест лежащие. Значит, треугольники FDK и BCK равны. Следовательно, их площади равны, то есть площадь трапеции равна площади треугольника ABF. Но из равенства треугольников также вытекает, что FK = BK, то есть AK — медиана в треугольнике ABF. Тогда треугольник KAB по площади составит половину треугольника FAB, а значит, и данной трапеции. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны. Поскольку угол ACB тупой, основания высот A1 и B1 будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA1B1B пересекаются, поэтому он выпуклый. Поскольку ∠AA1B = ∠AB1B = 90°, каждый из прямоугольных треугольников AA1B и AB1B вписан в окружность с диаметром AB. Это означает, что все вершины четырёхугольника AA1B1B лежат на одной окружности. Тогда углы ∠AB1A1 и ∠ABA1 равны как вписанные углы, опирающиеся на дугу A1A. Аналогично, ∠BA1B1 = ∠BAB1. Значит, указанные треугольники подобны по двум углам. Укажем общую теорему. Основания двух высот треугольника (остроугольного или тупоугольного) и одна из его вершин образуют треугольник, подобный исходному; коэффициент подобия равен модулю косинуса их общего угла. В треугольнике ABC с тупым углом АСВ проведены высоты АА1 и ВВ1. Докажите, что треугольники A1CB1 и АСВ подобны. 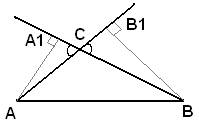
Рассмотрим сначала два прямоугольных треугольника AA1C и BB1C, которые подобны по двум углам (один угол у них прямой, а углы 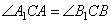 как вертикальные). У подобных треугольников AA1C и BB1C сторона A1C пропорциональна стороне B1C, а сторона AC пропорциональна стороне BC. как вертикальные). У подобных треугольников AA1C и BB1C сторона A1C пропорциональна стороне B1C, а сторона AC пропорциональна стороне BC. Рассмотрим теперь треугольники A1CB1 и ACB, у которых пропорциональны стороны AC, CB и A1C, B1C и равны углы 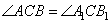 между этими сторонами как вертикальные. По второму признаку подобия два треугольника подобны, если стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника и углы, заключенные между этими сторонами, равны. То есть треугольники A1CB1 и ACB подобны друг другу. Утверждение доказано. между этими сторонами как вертикальные. По второму признаку подобия два треугольника подобны, если стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника и углы, заключенные между этими сторонами, равны. То есть треугольники A1CB1 и ACB подобны друг другу. Утверждение доказано. Сторона АВ параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны АВ. Докажите, что DK — биссектриса угла ADC. Проведём FK параллельно AD (см. рисунок). Тогда AD = AK = KB. Следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD делит угол ADC пополам. 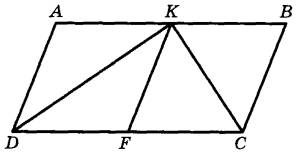
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники KAB и KCD подобны. 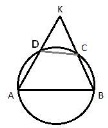
Если вокруг четырехугольника можно описать окружность, то суммы его противоположных углов равны по 180 градусов, то есть 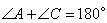 . Если положить угол . Если положить угол 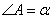 , тогда угол , тогда угол 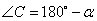 , и, учитывая, что углы , и, учитывая, что углы 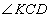 и и 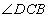 смежные, то угол смежные, то угол 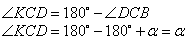
то есть он равен углу 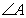 . Таким образом, треугольники KAB и KDC подобны по двум углам (угол K – общий). Утверждение доказано. . Таким образом, треугольники KAB и KDC подобны по двум углам (угол K – общий). Утверждение доказано. В остроугольном треугольнике ABC проведены высоты BB1 и CC1 Докажите, что углы BB1C1 и ВСC1 равны. 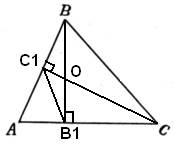
1. Из рисунка видно, что треугольники BOC1 и CB1O подобны по двум углам (углы 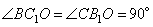 , так как CC1 и BB1 – высоты, а углы , так как CC1 и BB1 – высоты, а углы 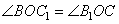 как вертикальные углы). В подобных треугольниках соответственные стороны пропорциональны, то есть можно написать соотношение как вертикальные углы). В подобных треугольниках соответственные стороны пропорциональны, то есть можно написать соотношение 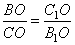 .2. Треугольники C1OB1 и BOC подобны по двум пропорциональным сторонам и углам между ними (углы .2. Треугольники C1OB1 и BOC подобны по двум пропорциональным сторонам и углам между ними (углы 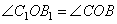 – вертикальные). 3. Из подобия треугольников следует равенство углов: – вертикальные). 3. Из подобия треугольников следует равенство углов:
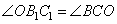 ,а, значит, равны и углы ,а, значит, равны и углы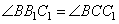
Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны. Треугольник CEF равен треугольнику DEF по трем сторонам, т.к. CE=DE (как радиусы одной окружности), EF – общая сторона (см. рисунок ниже). Тогда углы 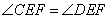 . . 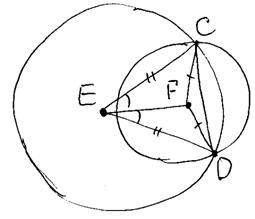 Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и 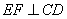
Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 6, а углы В и С четырёхугольника равны соответственно 124° и 116°. В четырехугольнике ABCD точка M – середина AD и равноудалена от вершин A, B, C и D. Следовательно, AM=MD=MB=MC. 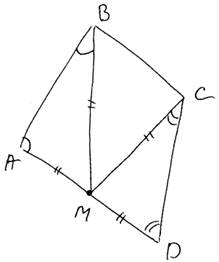
Пусть 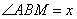 , тогда , тогда 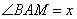 , так как треугольник AMB – равнобедренный с основанием AB. Также , так как треугольник AMB – равнобедренный с основанием AB. Также 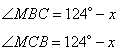
поэтому 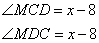
Учитывая, что сумма углов в любом треугольнике 180 градусов, имеем: 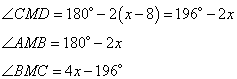
Рассмотрим треугольник BMC, в котором сумма углов равна 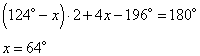
Следовательно, 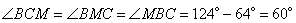
и треугольник BMC – равносторонний. Поэтому BM=BC=6 и AM=BM=6. Тогда сторона AD=2AM=2∙6=12. Ответ: 12. В трапеции ABCD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой CD, если, AD = 4, ВС = 2. Решение. Продлим стороны AB и CD так, чтобы они пересеклись в точке T. Пусть 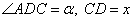 . По условию задания BC=2, AD=4, следовательно, . По условию задания BC=2, AD=4, следовательно, QD = AD-BC = 4-2 = 2 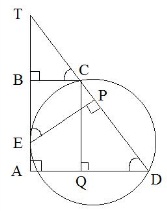
Из прямоугольного треугольника QCD, имеем: 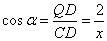
Тот же самый угол можно выразить и так: 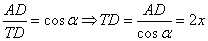
А, учитывая, что 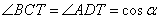 , можно записать отношение: , можно записать отношение: 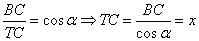
Далее, так как TE – касательная к окружности (по условию задания), а TD – секущая, то по теореме о касательной и секущей, имеем: 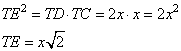
Треугольники TPE и TAD подобны по двум углам: 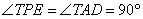 , угол T – общий. Значит, , угол T – общий. Значит,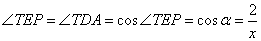 . Следовательно, . Следовательно, 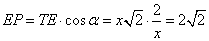
Ответ: 2√2. Окружности радиусов 12 и 20 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD. Решение. Так как AC и BD – касательные, то 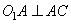 , , 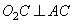 . Также . Также 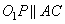 (так как ACPO1 – прямоугольник), следовательно, PO2=20-12=8, так как AO1=12, CO2=20. А расстояние между центрами окружностей O1O2=12+20=32. (так как ACPO1 – прямоугольник), следовательно, PO2=20-12=8, так как AO1=12, CO2=20. А расстояние между центрами окружностей O1O2=12+20=32. 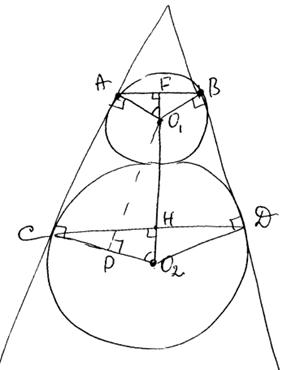
Рассмотрим прямоугольный треугольник O1PO2, из которого имеем: 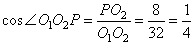
Углы 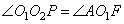 , так как они соответственные. Рассмотрим прямоугольный треугольник AFO1, в котором , так как они соответственные. Рассмотрим прямоугольный треугольник AFO1, в котором 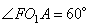 , следовательно, , следовательно, 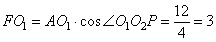 . Из прямоугольного треугольника CHO2 по аналогии, получаем: . Из прямоугольного треугольника CHO2 по аналогии, получаем: 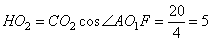 . Таким образом, расстояние между прямыми AB и CD, равно: . Таким образом, расстояние между прямыми AB и CD, равно: 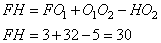
Ответ: 30.
Грузовик перевозит партию щебня массой 120 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 3 тонны щебня. Определите, сколько тонн щебня было перевезено за последний день, если вся работа была выполнена за 10 дней. Имеем арифметическую прогрессию с 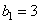 тонны щебня и суммой первых десяти ее членов, равной: тонны щебня и суммой первых десяти ее членов, равной: 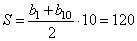 тонн тонн
Отсюда находим 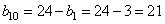 тонну тонну
Задание 11. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 80 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 24 секундам. Ответ дайте в метрах. Обозначим через 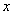 длину скорого поезда. Так как поезда движутся навстречу друг другу, то скорость прохождения поездов мимо друг друга составляет 80+40=120 км/ч. В задаче сказано, что поезда прошли мимо друг друга за 24 секунды (24/3600 часа). Это эквивалентно тому, что скорый поезд прошел за это время 350 метров (0,35 км) и еще свою длину. Получаем уравнение длину скорого поезда. Так как поезда движутся навстречу друг другу, то скорость прохождения поездов мимо друг друга составляет 80+40=120 км/ч. В задаче сказано, что поезда прошли мимо друг друга за 24 секунды (24/3600 часа). Это эквивалентно тому, что скорый поезд прошел за это время 350 метров (0,35 км) и еще свою длину. Получаем уравнение 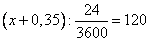
откуда имеем 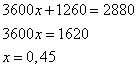
То есть длина скорого поезда 0,45 км или 450 метров. Задание 22. Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 3 км/ч навстречу поезду, за 30 секунд. Найдите длину поезда в метрах. Скорость обгона пешехода поездом, равна 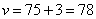 км/ч. км/ч.
С этой скоростью поезд обгонял пешехода в течение 30 секунд, то есть в течение 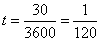 часа. Следовательно, длина поезда, равна часа. Следовательно, длина поезда, равна 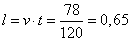 км км
что составляет 650 метров. Задание 22. Шесть одинаковых рубашек дешевле куртки на 8 %. На сколько процентов девять таких же рубашек дороже куртки? Шесть рубашек дешевле куртки на 8% означает, что 6 рубашек составляют 100-8=92% от стоимости куртки. Следовательно, одна рубашка – это  % от стоимости куртки. Таким образом, 9 рубашек будут составлять % от стоимости куртки. Таким образом, 9 рубашек будут составлять 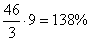 от стоимости куртки, т.е. будут на 38% дороже. от стоимости куртки, т.е. будут на 38% дороже. Задание 22. Баржа прошла по течению реки 72 км и, повернув обратно, прошла ещё 54 км, затратив на весь путь 9 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч. Обозначим через x км/ч – собственную скорость баржи. Тогда ее скорость по течению реки равна x+5 км/ч, а против течения – x-5 км/ч. Первые 72 км по течению она прошла за 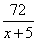 часов, а 54 км против течения за часов, а 54 км против течения за 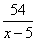 часов. Так как в пути она была 9 часов, то получаем следующее уравнение: часов. Так как в пути она была 9 часов, то получаем следующее уравнение: 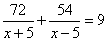 , ,
откуда 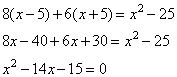
Решаем квадратное уравнение, имеем: 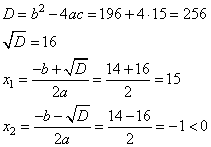
Так как скорость баржи величина положительная, то получаем значение 15 км/ч. В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора? Изначально в растворе содержится 24% вещества, то есть его объем в 10 литрах равен 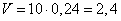 литров. После того как добавили 5 литров воды, концентрация раствора составила литров. После того как добавили 5 литров воды, концентрация раствора составила 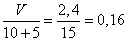 , ,
то есть 16%. Ответ: 16. Два автомобиля одновременно отправились в 420-километровый пробег. Первый едет со скоростью на 24 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. найдите скорость первого автомобиля 420/(x-24) - 420/x =2
(420*24)/(x²-24x) =2
10080/(x²-24x) =2
2*(x²-24x)-10080=0
2x²-48x-10080=0
x²-24x-5040=0
D=24²-4*(-5040)=576+20160=√20736=144
x=(24+144)/2=168/2=84км/ч скорость первого автомобиля
| Окружность пересекает стороны АВ и АС треугольника ABC в точках K и P соответственно и проходит через вершины В и С. Найдите длину отрезка KP, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ. Пусть сторона BC=x, тогда AB=2x, так как она в 2 раза больше стороны BC по условию задачи. Рассмотрим четырехугольник CPKB, который вписан в окружность. Как известно, у такого четырехугольника сумма противоположных углов равна 180 градусов, то есть 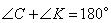 и и 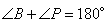 . Предположим, что угол . Предположим, что угол 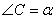 , тогда угол , тогда угол 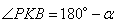 , теперь, учитывая, что углы , теперь, учитывая, что углы 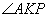 и и 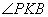 смежные, то угол смежные, то угол 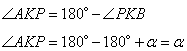
то есть он равен углу 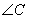 . Аналогично и для угла . Аналогично и для угла 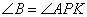 . Из равенства этих двух пар углов следует, что треугольники ACB и APK подобны друг другу по двум углам. . Из равенства этих двух пар углов следует, что треугольники ACB и APK подобны друг другу по двум углам. 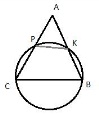
Для подобных треугольников можно записать следующее соотношение: 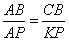 , ,
откуда 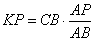
и подставляя числовые значения, имеем: 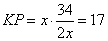 . .
Ответ: 17. Отрезки АВ и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если АВ = 20, CD = 48, а расстояние от центра окружности до хорды АВ равно 24. Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть, 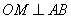 , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=20, то AM=10. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора: , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=20, то AM=10. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора: 
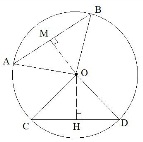
Также это означает, что OC=OD=AO=26. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=24. По теореме Пифагора находим длину OH: 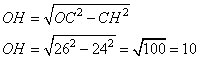
Ответ: 10 Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояния от центра окружности до хорд AB и CD равны соответственно 40 и 9. РЕШЕНИЕ:
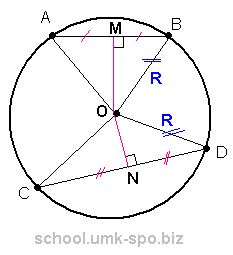
МВ = АВ/2 = 18/2 = 9
∆ВМО = ∆ OND ( OB=OD=R, MB = ON = 9) ⇒ ND = OM = 40
CD = 2 ND = 2 * 40 = 80
Ответ: 80 Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 15, АС = 25, NC = 22. 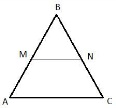
По условию задачи в треугольнике ABC прямая 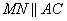 , следовательно, треугольники MBN и ABC подобны по двум углам: угол , следовательно, треугольники MBN и ABC подобны по двум углам: угол 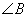 - общий, а углы - общий, а углы 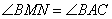 как соответственные при параллельных прямых MN, AC и секущей AB. Из подобия треугольников следует: как соответственные при параллельных прямых MN, AC и секущей AB. Из подобия треугольников следует: 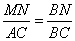 . .
Из рисунка видно, что 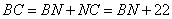 , подставляем числовые значения в отношение, имеем: , подставляем числовые значения в отношение, имеем: 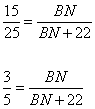
откуда 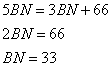
Ответ: 33.
В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны. 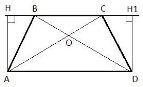
Запишем площадь треугольника ABO в виде: 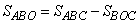 ,где ,где 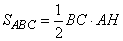 - площадь треугольника ABC; - площадь треугольника ABC; 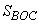 - площадь треугольника BOC. То есть площадь треугольника ABO можно представить как: - площадь треугольника BOC. То есть площадь треугольника ABO можно представить как:
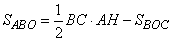 . (1) . (1)
Аналогично запишем площадь треугольника DCO, имеем: 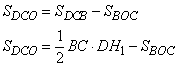
Так как 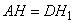 , то последнее выражение можно переписать в виде: , то последнее выражение можно переписать в виде: 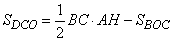 . (2) . (2)
Выражения (1) и (2) идентичны между собой и описывают площади треугольников ABO и DCO, то есть площади этих треугольников равны. Утверждение доказано. Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD. 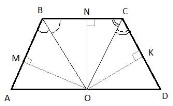
По условию задачи ABCD – трапеция с основаниями BC и AD и биссектрисами BO и CO, то есть углы 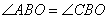 и и 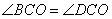 . Из точки O проведем три перпендикуляра . Из точки O проведем три перпендикуляра 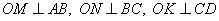 (по сути они будут являться расстояниями от точки O до прямых AB, BC и CD). (по сути они будут являться расстояниями от точки O до прямых AB, BC и CD). Теперь заметим, что треугольники BMO=BNO равны как прямоугольные по гипотенузе и острому углу: BO – общая гипотенуза; 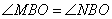 , так как BO – биссектриса. Из равенства треугольников следует, что OM=ON. , так как BO – биссектриса. Из равенства треугольников следует, что OM=ON. Аналогично для треугольников CNO=CKO, которые равны как прямоугольные по гипотенузе и острому углу: CO – общая гипотенуза; 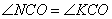 , так как CO – биссектриса. Следовательно, ON=OK. , так как CO – биссектриса. Следовательно, ON=OK. Таким образом, имеем, что MO=NO=KO, а значит, точка O равноудалена от прямых AB, BC и CD. Положение доказано. Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади параллелограмма. Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как 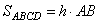 ,а площади треугольников как ,а площади треугольников как
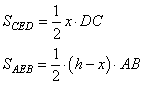 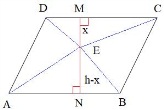
Так как в параллелограмме противоположные стороны равны, то AB=CD и сумма площадей треугольников равна 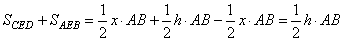 , ,
что в точности равно половине площади параллелограмма ABCD. Утверждение доказано. Окружности с центрами в точках I и J не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n. 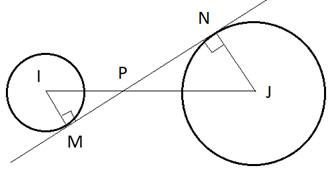
По условию задачи прямые IP:JP=m:n, а MN – касательная к окружностям в точках M и N, следовательно, 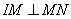 и и 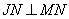 . Рассмотрим два прямоугольных треугольника IPM и JPN, которые подобны по двум углам: один угол у них прямой, а два других . Рассмотрим два прямоугольных треугольника IPM и JPN, которые подобны по двум углам: один угол у них прямой, а два других 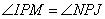 как вертикальные углы. Для подобных треугольников можно записать соотношение: как вертикальные углы. Для подобных треугольников можно записать соотношение: 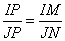 , ,
но по условию 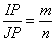 , следовательно, , следовательно, 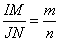
или, что эквивалентно, в виде  , ,
где 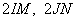 - диаметры соответствующих окружностей. Утверждение доказано. - диаметры соответствующих окружностей. Утверждение доказано. Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD. 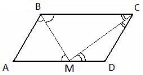
Так как ABCD – параллелограмм, то стороны 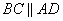 и и 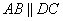 . Из этого положения следует равенство углов . Из этого положения следует равенство углов 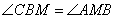 и и 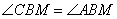 . Так как BM – биссектриса, то равны и углы . Так как BM – биссектриса, то равны и углы 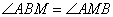 . Из равенства двух углов при основании BM следует, что треугольник ABM – равнобедренный, с равными сторонами AB=AM. Аналогично для треугольника CMD, у которого углы при основании MC равны, следовательно, он равнобедренный и CD=MD. Учитывая, что ABCD – параллелограмм, у которого стороны AB=CD, то автоматически следует, что и AM=MD, то есть точка M – середина отрезка AD. Положение доказано. . Из равенства двух углов при основании BM следует, что треугольник ABM – равнобедренный, с равными сторонами AB=AM. Аналогично для треугольника CMD, у которого углы при основании MC равны, следовательно, он равнобедренный и CD=MD. Учитывая, что ABCD – параллелограмм, у которого стороны AB=CD, то автоматически следует, что и AM=MD, то есть точка M – середина отрезка AD. Положение доказано.
В треугольнике ABC биссектриса угла А делит высоту, проведённую из вершины В, в отношении 5 : 4, считая от точки В. Найдите радиус окружности, описанной около треугольника ABC, если ВС = 12. 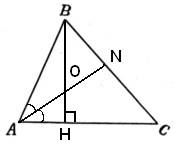 По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть 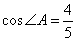 . Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим . Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим
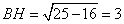 . .
Тогда синус угла A равен 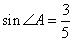 . По следствию теоремы синусов имеем: . По следствию теоремы синусов имеем: 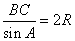 , ,
где R – радиус описанной окружности. Следовательно,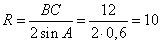 . . Ответ: 10. Четырёхугольник ABCD со сторонами АВ=11 и CD = 41 вписан в окружность. Диагонали АС и BD пересекаются в точке К, причём угол AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника. Углы 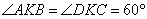 как вертикальные. Проведем отрезок DN параллельный отрезку AC. В этом случае как вертикальные. Проведем отрезок DN параллельный отрезку AC. В этом случае 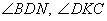 - накрест лежащие при параллельных прямых AC и DN и секущей BD. - накрест лежащие при параллельных прямых AC и DN и секущей BD. 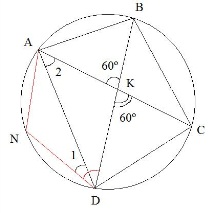
Четырехугольник DNAB вписан в окружность, следовательно, 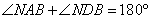
откуда 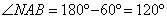
Далее, 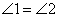 как накрест лежащие при параллельных прямых AC, DN и секущей AD, следовательно, дуга AN равна дуге DC, откуда AN=DC=30. как накрест лежащие при параллельных прямых AC, DN и секущей AD, следовательно, дуга AN равна дуге DC, откуда AN=DC=30. Рассмотрим треугольник NAB вписанный в окружность. По теореме косинусов, имеем: 
По теореме синусов можно записать: 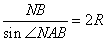 , ,
где R – радиус описанной окружности. Из последнего выражения: 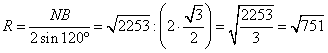
Боковые стороны АВ и CD трапеции ABCD равны соответственно 16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны АВ. Найдите площадь трапеции. Пусть М — середина АВ (см. рис.). Продолжим биссектрису DM угла ADC до пересечения с продолжением основания ВС в точке K. Поскольку 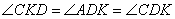 , треугольник KCD — равнобедренный, KC = CD = 34. Тогда KB = КС - ВС = 34 - 2 = 32. , треугольник KCD — равнобедренный, KC = CD = 34. Тогда KB = КС - ВС = 34 - 2 = 32. 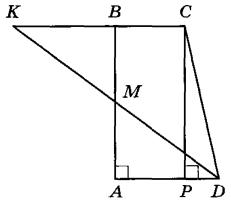
Из равенства треугольников AMD и ВМК следует, что AD = BK = 32. Проведём через вершину C прямую, параллельную стороне AB, до пересечения с основанием AD в точке P. Треугольник CPD — прямоугольный, так как 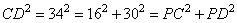
Поэтому CP — высота трапеции. Следовательно, 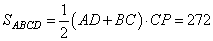 Медиана ВМ треугольника ABC является диаметром окружности, проходящей через середину отрезка ВС. Найдите длину стороны АС, если радиус окружности, описанной около треугольника ABC, равен 11. Окружность проходит через точку F с диаметром BM (где BM – медиана треугольника ABC). Следовательно, точка M – точка касания, а AC – касательная к малой окружности. Отсюда получаем, что 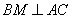 и треугольник BAM – равнобедренный с AB=BC, BM – биссектриса угла B. и треугольник BAM – равнобедренный с AB=BC, BM – биссектриса угла B. 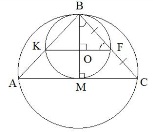
Точка O – центр окружности и середина отрезка BM. Точка F – середина отрезка BC, значит, OF – средняя линия треугольника BMC и 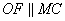 . Треугольник BOF – равнобедренный, следовательно, углы . Треугольник BOF – равнобедренный, следовательно, углы 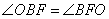 и с учетом и с учетом 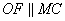 , имеем: , имеем: 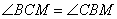 , значит, треугольник BMC – прямоугольный и равнобедренный с BM=MC. В таком треугольнике углы при основании равны по 45º: , значит, треугольник BMC – прямоугольный и равнобедренный с BM=MC. В таком треугольнике углы при основании равны по 45º: 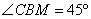 . И, так как BM – биссектриса угла B, получаем, что . И, так как BM – биссектриса угла B, получаем, что 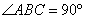 . Треугольник ABC может иметь угол B=90º только при условии, что AC – диаметр большой окружности, описанной вокруг треугольника ABC. . Треугольник ABC может иметь угол B=90º только при условии, что AC – диаметр большой окружности, описанной вокруг треугольника ABC. По условию задания радиус описанной окружности равен R=11, значит, 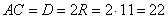
Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов? Пусть 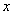 кг фруктов требуется для приготовления 21 кг высушенных фруктов. Так как в фруктах содержится 93% воды, то процент сухого вещества составляет 100-93=7%, и в x кг сухого вещества равно кг фруктов требуется для приготовления 21 кг высушенных фруктов. Так как в фруктах содержится 93% воды, то процент сухого вещества составляет 100-93=7%, и в x кг сухого вещества равно 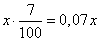 кг. кг.
Масса сухого вещества в высушенных 21 кг фруктах составляет 100-16=84% и равна 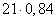 кг. По условию задачи величина кг. По условию задачи величина 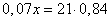 , откуда находим: , откуда находим: 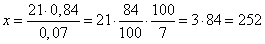 кг. кг.
Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Обозначим условно первую половину пути за 1, и вторую половину пути за 1. Соответственно, весь путь будет равен S=1+1=2. Время, затраченное автомобилем на прохождение первой половины пути, равно: 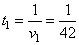 часов, часов,
а вторую половину пути за 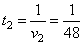 часов. часов.
Общее время в пути составило 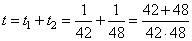 часов. часов.
Среднюю скорость можно найти как отношение пути ко времени, проведенном в этом пути, то есть: 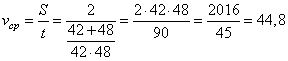
. Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 100 км — со скоростью 50 км/ч, а последние 165 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Весь путь составил S=500+100+165=765 км. Вычислим время, за которое автомобиль прошел этот путь: 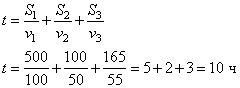
Таким образом, его средняя скорость, равна: 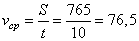 км/ч. км/ч.
Смешали 4 литра 35-процентного раствора вещества с 11 литрами 5-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? После смешивания объем получившегося раствора равен V=4+11=15 литров. Значит, доля 35-процентного раствора в этом объеме составляет 4/V, а доля 5-процентного раствора – 11/V. Получаем концентрацию получившегося раствора: 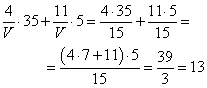
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Обозначим через x км/ч скорость велосипедиста на пути из A в B. Так как расстояние между пунктами A и B составляет 60 км, то время, которое затратил велосипедист, чтобы проехать это расстояние, равно 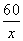 часов. На обратном пути его скорость увеличилась на 10 км/ч и составила x+10 км/ч, следовательно, он затратил на обратный путь часов. На обратном пути его скорость увеличилась на 10 км/ч и составила x+10 км/ч, следовательно, он затратил на обратный путь 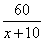 . В задаче сказано, что на обратном пути он сделал остановку на 3 часа, следовательно, в сумме (с учетом остановки) на обратный путь было потрачено . В задаче сказано, что на обратном пути он сделал остановку на 3 часа, следовательно, в сумме (с учетом остановки) на обратный путь было потрачено 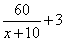 часа. Учитывая, что время, потраченное на путь из A в B и на обратный путь равны, получаем уравнение: часа. Учитывая, что время, потраченное на путь из A в B и на обратный путь равны, получаем уравнение: 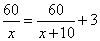 . .
Упростим выражение, перепишем его в виде: 
Решаем квадратное уравнение, получаем два корня: 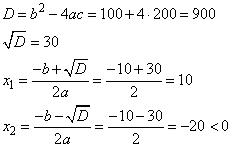
Так как скорость велосипедиста величина положительная, получаем его скорость 10 км/ч. Коля и Митя выполняют одинаковый тест. Коля отвечает за час на 12 вопросов теста, а Митя — на 21. Они одновременно начали отвечать на вопросы теста, и Коля закончил свой тест позже Мити на 105 минут. Сколько вопросов содержит тест? Пусть в тесте 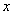 вопросов. Тогда общее время ответа Коли на все вопросы равно вопросов. Тогда общее время ответа Коли на все вопросы равно 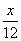 часов, а общее время ответа Мити часов, а общее время ответа Мити 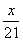 часов. Известно, что Коля отвечал на тест на 105 минут (7/4 часа) дольше Мити. Имеем уравнение часов. Известно, что Коля отвечал на тест на 105 минут (7/4 часа) дольше Мити. Имеем уравнение 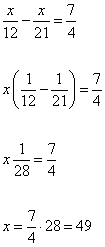
То есть в тесте 49 вопросов.
| Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке K. Найдите периметр параллелограмма, если ВК = 3, CK = 19. 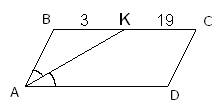
Так как ABCD – параллелограмм, то стороны 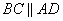 , следовательно, углы , следовательно, углы 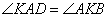 как накрест лежащие при параллельных прямых BC, AD и секущей AK. По условию задачи AK – биссектриса угла A, значит, углы как накрест лежащие при параллельных прямых BC, AD и секущей AK. По условию задачи AK – биссектриса угла A, значит, углы 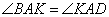 и отсюда получаем, что и отсюда получаем, что 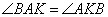 . Таким образом, треугольник ABK равнобедренный со сторонами AB=BK=3 и основанием AK. Учитывая, что в параллелограмме противоположные стороны равны, и BC=3+19=22, то периметр равен . Таким образом, треугольник ABK равнобедренный со сторонами AB=BK=3 и основанием AK. Учитывая, что в параллелограмме противоположные стороны равны, и BC=3+19=22, то периметр равен 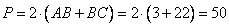 . .
Ответ: 50. Углы В и С треугольника ABC равны соответственно 66° и 84°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 15. 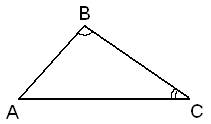
Так как сумма углов в любом треугольнике равна 180 градусов, то угол А равен 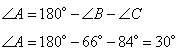
Найдем длину BC из теоремы синусов как 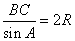 , ,
где 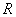 - радиус описанной окружности вокруг треугольника ABC. Отсюда получаем: - радиус описанной окружности вокруг треугольника ABC. Отсюда получаем: 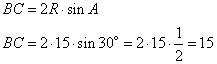
Ответ: 15. Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, a CD = 26. 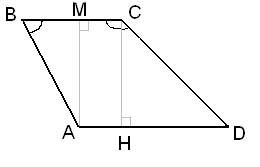
Рассмотрим прямоугольный треугольник CDH, в котором угол 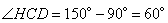 . Так как косинус угла – это отношение прилежащего катета к гипотенузе, то можно записать, что . Так как косинус угла – это отношение прилежащего катета к гипотенузе, то можно записать, что 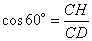 , ,
откуда 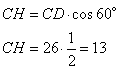
Рассмотрим прямоугольный треугольник ABM, в котором AM=CH. Известно, что синус угла – это отношение противолежащего катета к гипотенузе, то есть, имеем: 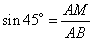 , ,
откуда 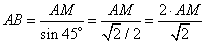 . .
Подставляя вместо AM найденное ранее числовое значение, получаем: 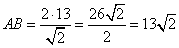 . .
Ответ: 13√2. Катет и гипотенуза прямоугольного треугольника равны 16 и 34 соответственно. Найдите высоту, проведённую к гипотенузе. 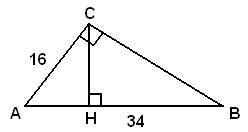
В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать: 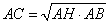
или в виде 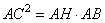 , ,
откуда 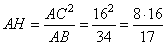 . .
Рассмотрим прямоугольный треугольник ACH, в котором известна гипотенуза AC и катет AH, следовательно, высоту CH можно найти по теореме Пифагора: 
Ответ: 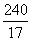 . . Окружность с центром на стороне АС треугольника ABC проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ = 2, АС = 8. Сделаем построение, проведен радиус BO, который будет перпендикулярен стороне AB, так как AB – касательная к окружности по условию задачи (см. рисунок). 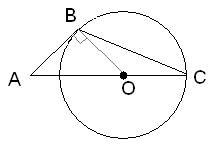
Введем обозначение OB=OC=r – радиусы окружности. Тогда отрезок 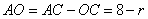 . Выразим квадрат радиуса BO=r из прямоугольного треугольника ABO по теореме Пифагора, получим следующее выражение: . Выразим квадрат радиуса BO=r из прямоугольного треугольника ABO по теореме Пифагора, получим следующее выражение: 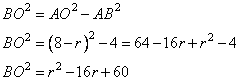
Так как BO=r, получаем уравнение: 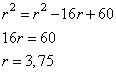
И диаметр окружности равен 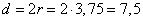 . . На средней линии трапеции ABCD с основаниями AD и ВС выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади трапеции. Доказательство проведем от обратного. Докажем сначала, что сумма площадей треугольников BEC и AED составляет половину площади трапеции. Это же автоматические будет означать, что оставшаяся площадь (сумма площадей треугольников AEB и CED) также будет равна половине площади трапеции. 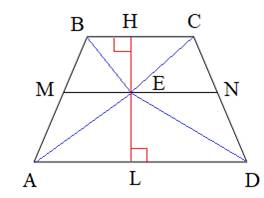
По условию задачи точка E лежит на отрезке MN – средней линии трапеции. Проведем через эту точку высоту HL трапеции. Тогда по определению средней линии, отрезки EH=EL=1/2∙HL. Используя данные обозначения, выразим площади треугольников BEC и AED следующим образом: 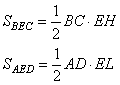
Соответственно, сумма этих площадей составит величину, равную 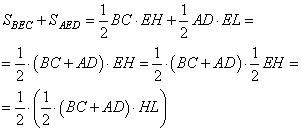
но так как 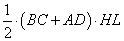 - это площадь всей трапеции, то получаем, что - это площадь всей трапеции, то получаем, что 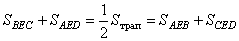 . .
Положение доказано. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны. 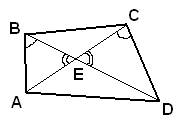
Проведем в четырехугольнике диагонали AC и BD и отметим точку E на их пересечении. Рассмотрим треугольники ABE и DEC, у которых равны углы 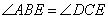 по условию задачи, а также равны углы по условию задачи, а также равны углы 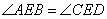 как вертикальные. Таким образом, треугольники ABE и DEC подобные по двум углам с пропорциональными сторонами BE и CE, а также AE и DE. Рассмотрим теперь треугольники AED и BEC, у которых сторона AE пропорциональна стороне DE, а сторона BE пропорциональна стороне CE, кроме того, равны углы как вертикальные. Таким образом, треугольники ABE и DEC подобные по двум углам с пропорциональными сторонами BE и CE, а также AE и DE. Рассмотрим теперь треугольники AED и BEC, у которых сторона AE пропорциональна стороне DE, а сторона BE пропорциональна стороне CE, кроме того, равны углы  как вертикальные. Отсюда следует, что треугольники AED и BEC подобны по двум соответствующим пропорциональным сторонам и углу между ними. Так как у подобных треугольников соответствующие углы равны, то угол как вертикальные. Отсюда следует, что треугольники AED и BEC подобны по двум соответствующим пропорциональным сторонам и углу между ними. Так как у подобных треугольников соответствующие углы равны, то угол 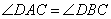 . Утверждение доказано. . Утверждение доказано. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны АВ и CD в точках Р и Т соответственно. Докажите, что BP = DT. 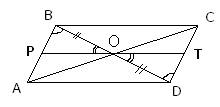
У параллелограмма диагонали BD и AC делятся в точке пересечения O пополам, то есть BO=OD. Кроме того, в параллелограмме противоположные стороны параллельны, то есть 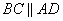 и, следовательно, и, следовательно, 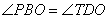 - как накрест лежащие при параллельных прямых и секущей BD. Углы - как накрест лежащие при параллельных прямых и секущей BD. Углы 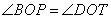 - как вертикальные углы. В результате имеем, что треугольники BOP и DOT равны по стороне и двум прилежащим к ней углам, а, следовательно, равны и стороны BP=DT. - как вертикальные углы. В результате имеем, что треугольники BOP и DOT равны по стороне и двум прилежащим к ней углам, а, следовательно, равны и стороны BP=DT. В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 6:7, Прямая AK пересекает сторону ВС в точке Р. Найдите отношение площади треугольника BKP к площади треугольника ABK. Медиана KM разбивает треугольник AKC на два равновеликих треугольника — пусть их площади равны по 7S. 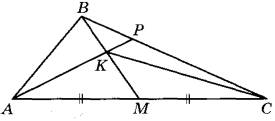
Поскольку 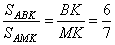 , получаем, что , получаем, что 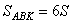 . Пусть . Пусть 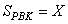 и и 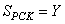 . Тогда . Тогда 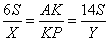 , отсюда , отсюда 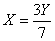 . Далее . Далее 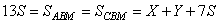
тогда  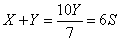 ,то есть ,то есть 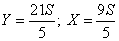 . Получаем, что . Получаем, что
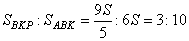
Ответ: 3:10 В трапеции ABCD основания AD и ВС равны соответственно 34 и 14, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ=12. Продлим боковые стороны трапеции до пересечения в точке Р (см. рис.). 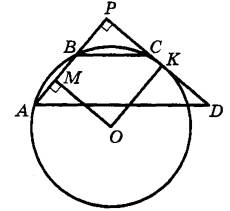
Из условия ясно, что 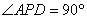 . Из подобия треугольников APD и ВРС получаем, что . Из подобия треугольников APD и ВРС получаем, что 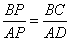 ,то есть ,то есть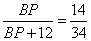
откуда BP = 8,4. Пусть окружность касается прямой CD в точке K, а O — её центр. Опустим из точки O перпендикуляр OM на хорду АВ. Точка М — середина АВ. Так как OMPK — прямоугольник, искомый радиус 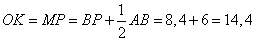
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 6, а расстояние от точки K до стороны АВ равно 6. 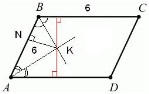
Так как ABCD параллелограмм, а AK и BK – биссектрисы углов A и B, то точка K равноудалена от сторон AB и BC (см. рисунок). По условию задачи точка K удалена от стороны AB на расстояние 6 единиц, следовательно, от стороны BC она также удалена на 6 единиц. Получаем, что высота параллелограмма (красная линия на рисунке) равна 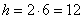 единиц. Тогда площадь параллелограмма можно найти как единиц. Тогда площадь параллелограмма можно найти как 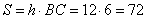 . .
Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если 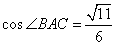 . . 1. Треугольник AFM подобен треугольнику ANF по двум углам (угол A – общий, а 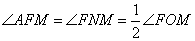 ). Отсюда следует, что ). Отсюда следует, что 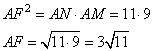
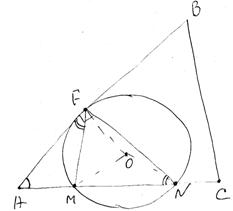
2. Рассмотрим треугольник AFM. По теореме косинусов находим FM: 
То есть, треугольник AFM – равнобедренный с основанием AF. Соответственно, углы при основании такого треугольника равны, получаем, 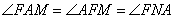 , откуда , откуда 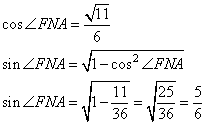
и 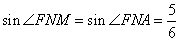 . . 3. Рассмотрим треугольник FMN. По теореме синусов, имеем: 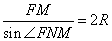 , ,
где R – радиус описанной окружности. Откуда: 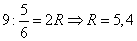
Два велосипедиста одновременно отправляются в пробег протяжённостью 208 км. Первый едет со скоростью на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Обозначим через x км/ч скорость первого велосипедиста. Тогда скорость второго будет равна x-3 км/ч. Путь в 208 км первый проходит за 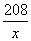 часов, а второй за часов, а второй за 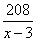 часов. Известно, что разница во времени прибытия на финиш составляет 3 часа. Получаем уравнение: часов. Известно, что разница во времени прибытия на финиш составляет 3 часа. Получаем уравнение: 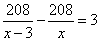 ,откуда ,откуда
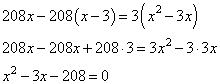
Решаем квадратное уравнение, получаем: 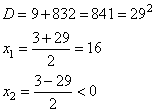
Имеем одно положительное значение x=16 км/ч. Это скорость первого велосипедиста. Скорость второго равна 16-3=13 км/ч. Задание 22. Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60 % кислоты. Сколько килограммов кислоты содержится во втором растворе? Пусть x% - концентрация первого раствора и y% - концентрация второго раствора. Тогда величину кислоты, содержащейся в первом растворе можно определить как 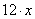 , а во втором растворе как , а во втором растворе как 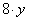 . В задаче сказано, что если объединить эти два раствора, то получится раствор 65% кислоты, то есть величина кислоты в объединенном растворе будет равна . В задаче сказано, что если объединить эти два раствора, то получится раствор 65% кислоты, то есть величина кислоты в объединенном растворе будет равна 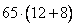 . Имеем уравнение . Имеем уравнение 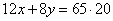 . .
Также в задаче сказано, что при равных объемах растворов получается раствор 60% кислоты, то есть можно записать, что 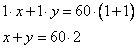 Получаем систему двух уравнений: Получаем систему двух уравнений:
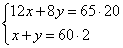 Умножим второе уравнение на 12 Умножим второе уравнение на 12
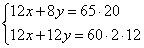 и вычтем из первого, получим: и вычтем из первого, получим:
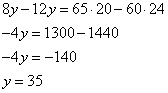 Таким образом, второй раствор имеем концентрацию 35% и кислоты во втором растворе равно Таким образом, второй раствор имеем концентрацию 35% и кислоты во втором растворе равно

Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун пробежал первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 5 км/ч меньше скорости второго. Пусть x км/ч скорость первого бегуна, тогда скорость второго x+5 км/ч. Известно, что спустя 45 минут (3/4 часа) второй бегун пробежал один круг, то есть длина круга 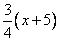 км. Первому бегуну через час бега оставалось пробежать еще 1 км до окончания круга, то есть за час он пробежал км. Первому бегуну через час бега оставалось пробежать еще 1 км до окончания круга, то есть за час он пробежал 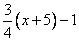 км. Эта величина также равна и скорости первого бегуна, так как она показывает расстояние, пройденное за 1 час. В то же время, скорость первого бегуна обозначена как x км/ч, следовательно, км. Эта величина также равна и скорости первого бегуна, так как она показывает расстояние, пройденное за 1 час. В то же время, скорость первого бегуна обозначена как x км/ч, следовательно, 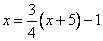 , ,
откуда имеем: 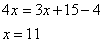
То есть скорость первого бегуна 11 км/ч. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий? Обозначим через x деталей в час – производительность второго рабочего, тогда первый рабочий выполняет x+9 деталей в час. Известно, что 112 деталей первый выполняет быстрее, чем второй, то есть 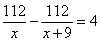 , ,
откуда 
Решаем квадратное уравнение, получаем: 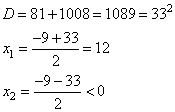
Так как выработка не может быть отрицательным числом, получаем производительность второго рабочего 12 деталей в час.
| Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника ABC к гипотенузе АС. Найдите АВ, если АН = 10, АС = 40. 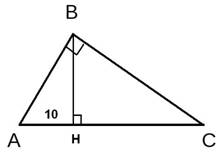
В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать: 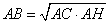 , ,
и, подставляя числовые значения, имеем: 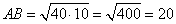 . .
Ответ: 20. Точка Н является основанием высоты ВН, проведённой из вершины прямого угла В прямоугольного треугольника ABC. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК = 12. 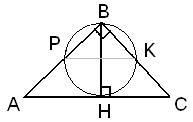
Для решения данной задачи нужно вспомнить, что в любой окружности хорды, проведенные от ее диаметра, всегда пересекаются под углом в 90 градусов. Следовательно, точки P и K находятся на разных концах диаметра окружности, и так как PK=12, то и диаметр окружности равен 12. В задаче сказано, что BH – это диаметр окружности, значит, BH=PK=12. Ответ: 12. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 24, BF = 18. 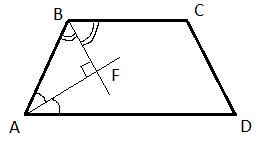 У трапеции ABCD основания У трапеции ABCD основания 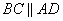 , следовательно, углы , следовательно, углы 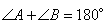 как внутренние односторонние при параллельных прямых. По условию задачи AF и BF – биссектрисы соответствующих углов, тогда сумма углов как внутренние односторонние при параллельных прямых. По условию задачи AF и BF – биссектрисы соответствующих углов, тогда сумма углов
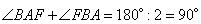
и, следовательно, угол 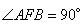 (так как сумма углов в треугольнике ABF равна 180 градусов). Таким образом, имеем прямоугольный треугольник AFB с гипотенузой AB, которую вычислим по теореме Пифагора: (так как сумма углов в треугольнике ABF равна 180 градусов). Таким образом, имеем прямоугольный треугольник AFB с гипотенузой AB, которую вычислим по теореме Пифагора: 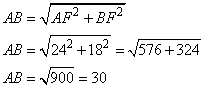
Ответ: 30. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, DC = 48, АС = 35. 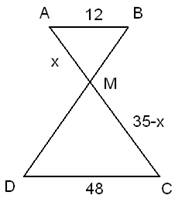
Так как 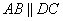 , то углы , то углы 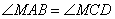 как накрест лежащие углы при параллельных прямых AB, DC и секущей AC. Углы как накрест лежащие углы при параллельных прямых AB, DC и секущей AC. Углы 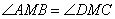 как вертикальные углы. Следовательно, треугольники AMB и CMD подобны по двум углам. Для подобных треугольников можно записать следующее отношение: как вертикальные углы. Следовательно, треугольники AMB и CMD подобны по двум углам. Для подобных треугольников можно записать следующее отношение: 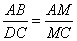 . .
Пусть AM=x, тогда MC=AC-AM=35-x, и отношение примет вид: 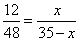 , ,
откуда 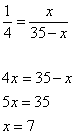
и MC=35-7=28. Ответ: 28. Высота АН ромба ABCD делит сторону CD на отрезки DH = 20 и СН = 5. Найдите высоту ромба. 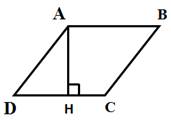
Решение. Длина стороны DC ромба ABCD, равна DC=DH+HC=20+5=25. Так как у ромба все стороны равны, то AD=DC=25. В результате, имеем прямоугольный треугольник, ADH, в котором известна гипотенуза AD и катет DH. Тогда второй катет AH (высота ромба) можно найти по теореме Пифагора: 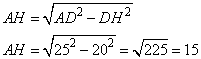
Ответ: 15. Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD = 6. Докажите, что треугольники CBD и BDA подобны. 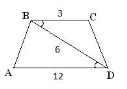 Так как ABCD трапеция, то ее основания 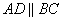 , следовательно, равны и углы , следовательно, равны и углы 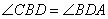 как накрест лежащие при параллельных BC, AD и секущей BD. Рассмотрим треугольники CBD и BDA, у которых имеем следующие пропорции: как накрест лежащие при параллельных BC, AD и секущей BD. Рассмотрим треугольники CBD и BDA, у которых имеем следующие пропорции: 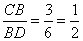 и и 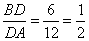 . . Следовательно, треугольники CBD и BDA подобны друг другу по двум пропорциональным сторонам и равным углам, заключенными между этими сторонами. Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 9 и MB = 12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD. 1. Так как CM – биссектриса, то по свойству биссектрисы: 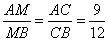 ,откуда ,откуда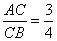 . .
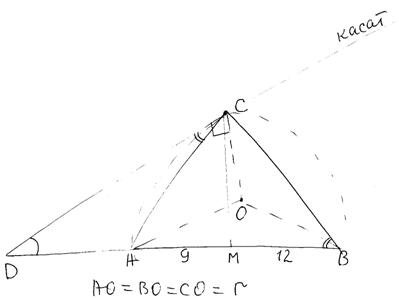
2. Угол ABC – вписанный и опирается на дугу AC, поэтому, угол ABC в 2 раза меньше градусной меры дуги AC: 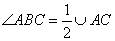 и и 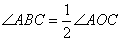 . . Угол ACD – это угол между касательной и хордой, следовательно, 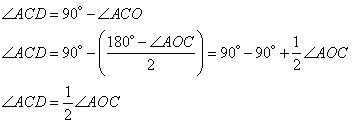
И получаем, что 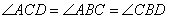 , а треугольники CDB и ADC подобны по двум углам (так как угол D – общий). Для подобных треугольников можно записать следующее отношение: , а треугольники CDB и ADC подобны по двум углам (так как угол D – общий). Для подобных треугольников можно записать следующее отношение: 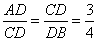 , ,
откуда 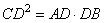 и и 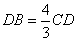 . .
Так как AD = DB-21, имеем: 
Ответ: 36. В параллелограмме ABCD проведена диагональ АС. Точка О является центром окружности, вписанной в треугольник ABC. Расстояния от точки О до точки А и прямых AD и АС соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD. 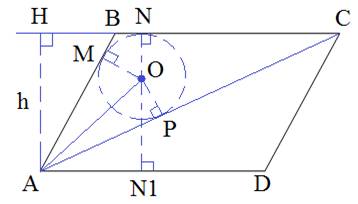
Окружность вписана в треугольник ABC с радиусами OM=ON=OP и перпендикулярными сторонам AB, BC, AC соответственно. По теореме об отрезках касательных, имеем: MB=BN, AM=AP, CN=CP. Пусть BM=BN=x, а CN=CP=y. Тогда BC=AD=x+y. Отрезок NN1=AH=17+7=24. Рассмотрим прямоугольный треугольник AMO. По теореме Пифагора найдем сторону AM: 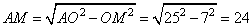
Значит, AP=AM=24. Найдем величину x+y из формулы площади треугольника ABC: 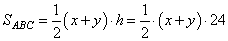
Эту же площадь можно вычислить как 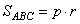 , ,
где 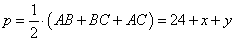 - полупериметр треугольника ABC; r=7 – радиус вписанной окружности. Приравниваем площади, получаем уравнение: - полупериметр треугольника ABC; r=7 – радиус вписанной окружности. Приравниваем площади, получаем уравнение: 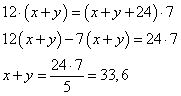
Значит, BC=AD=33,6 и площадь параллелограмма, равна: 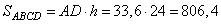
Ответ: 806,4 На стороне ВС остроугольного треугольника ABC (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М, AD = 80, MD = 64, Н — точка пересечения высот треугольника ABC. Найдите АН. AD – высота треугольника ABC, значит, 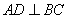 . Учитывая, что MQ – хорда, с которой радиус окружности составляет 90º, то точка D делит MQ пополам и MD=DQ=64. . Учитывая, что MQ – хорда, с которой радиус окружности составляет 90º, то точка D делит MQ пополам и MD=DQ=64. 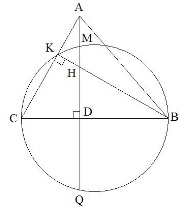
Следовательно, AM = AD-MD = 80-64=16, а AQ = AD+DQ = 80+64 = 144 По следствию из теоремы о касательной и секущей, имеем: 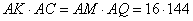
Треугольники AKH и ADC подобны по двум углам: 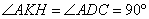 , а угол CAD – общий. Следовательно, , а угол CAD – общий. Следовательно, 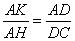
откуда 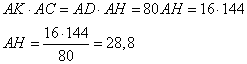
Ответ: 28,8 Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 2 минуты, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 277 км, скорость первого велосипедиста равна 16 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи. Обозначим через x км – расстояние от города, из которого выехал второй велосипедист, до точки встречи. Тогда первый велосипедист проехал 277-x км. Время, которое потратил второй велосипедист в пути, составило 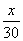 часов, а первого – часов, а первого – 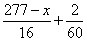 часа. Так как оба велосипедиста выехали одновременно навстречу друг другу, то к моменту их встречи они находились в пути одинаковое время. Имеем уравнение: часа. Так как оба велосипедиста выехали одновременно навстречу друг другу, то к моменту их встречи они находились в пути одинаковое время. Имеем уравнение: 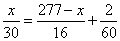 . .
Упрощаем, находим x, получаем: 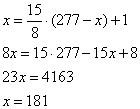
То есть второй велосипедист проехал 181 км до момента встречи с первым велосипедистом. Ответ: 181. Задание 11. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч. Обозначим через x км/ч скорость течения. Тогда при движении ложки против течения, ее скорость была равна 11-x км/ч и на преодоления 112 км было потрачено 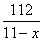 часов. При обратном движении лодка шла по течению, то есть ее скорость была равна 11+x км/ч и на преодоления 112 км было затрачено часов. При обратном движении лодка шла по течению, то есть ее скорость была равна 11+x км/ч и на преодоления 112 км было затрачено 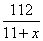 часов. Известно, что на обратный путь было потрачено на 6 часов меньше. Имеем уравнение: часов. Известно, что на обратный путь было потрачено на 6 часов меньше. Имеем уравнение: 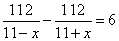 , ,
откуда 
Решаем квадратное уравнение получаем два корня: 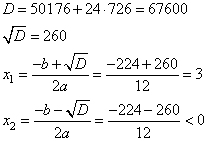
Получаем один положительный корень x=3 км/ч. Ответ: 3. Задание 22. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 1 км/ч. Решение. Пусть x км/ч – скорость лодки в неподвижной воде. Тогда скорость лодки против течения равна x-1 км/ч, а по течению x+1 км/ч. Сначала лодка плыла против течения 255 км, то есть затратила на этот путь 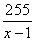 часов. Затем, она проделала тот же путь по течению и затратила на него часов. Затем, она проделала тот же путь по течению и затратила на него 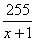 часов. Известно, что на обратный путь она затратила на 2 часа меньше, имеем: часов. Известно, что на обратный путь она затратила на 2 часа меньше, имеем: 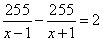 . .
Упрощаем, получаем: 
То есть собственная скорость лодки равна 16 км/ч. Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем вторая труба? Пропускную способность первой трубы обозначим через 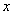 . Тогда вторая труба будет пропускать . Тогда вторая труба будет пропускать 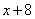 литров воды. Время заполнения объема в 180 литров первой трубы составляет литров воды. Время заполнения объема в 180 литров первой трубы составляет 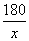 , а тот же объем для второй трубы , а тот же объем для второй трубы 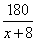 . По условию задачи сказано, что вторая труба заполняет данный объем на 8 минут быстрее первой. Получаем уравнение . По условию задачи сказано, что вторая труба заполняет данный объем на 8 минут быстрее первой. Получаем уравнение 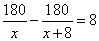
откуда имеем: 
Решаем квадратное уравнение, получаем корни 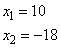
Так как отрицательного значения быть не может, остается одно значение 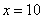 . . Ответ: 10.
|









 Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и
Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и 


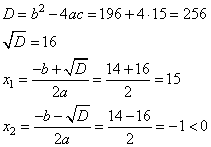


 По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть
По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть