17
Оглавление
|
| Введение | 3 |
| Глава 1 | Теоретические аспекты иследования | 5 |
| 1.1 | История открытия флексагона | 5 |
| 1.2 | Виды флексагонов и их классификация | 7 |
| 1.3 | Применение флексагонов | 9 |
| Глава 2 | Практические аспекты исследования | 11 |
| 2.1 | Конструирование флексагонов | 11 |
| 2.1.1 | Тригексафлексагон | 11 |
| 2.1.2 | Гексагексафлексагон | 12 |
| 2.1.3 | Тритетрафлексагон | 13 |
| 2.1.4 | Тетратетрафлексагон | 14 |
| 2.1.5 | Гексатетрафлексагон | 15 |
| 2.2 | Разворачивание флексагонов | 17 |
|
| Заключение | 20 |
|
| Список использованной литературы | 21 |
Введение
Все мы любим занимательную математику. Занимательная математика пробуждает наблюдательность, умение логически мыслить, веру в свои силы. Элемент игры, который делает занимательную математику занимательной, может иметь форму головоломки, состязания, фокуса, парадокса и т.д.
Не так уж велико различие между восторгом человека, сумевшего найти ключ к сложной головоломке, и радостью математика, преодолевшего еще одно препятствие на пути к решению сложной научной проблемы. И тот и другой заняты поисками истиной красоты – того ясного, четко определенного, загадочного и восхитительного порядка, что лежит в основе всех явлений. Неудивительно поэтому, что чистую математику порой трудно отличить от занимательной.
Многие считают, что математика не интересна и состоит только из формул, задач, решений и уравнений. Мы хотим продемонстрировать своей работой, что математика разноплановая наука, и главная цель – показать, что математика очень удивительный и необычный предмет для изучения.
Мы приглашаем вас на короткую экскурсию в загадочный мир флексагонов.
Актуальность: флексагоны способствуют развитию пространственного воображения и имеют практическое применение.
Цель: изучить мир флексагонов и показать, что головоломки бывают не только из дерева и железа - привычных для нас форм, но и из бумаги, которые мы можем сделать своими руками.
Объект
: математические поверхности.
Предмет: флексагоны
Задачи:
Изучить информацию о флексагонах;
Изучить схемы для складывания флексагонов;
Рассмотреть применение флексагонов в жизни человека;
Научиться создавать модели флексагонов.
Гипотеза: элемент игры, который делает занимательную математику занимательной, может иметь форму головоломки, фокуса, парадокса…
Методы:
Глава 1. Теоретические аспекты исследования
История открытия флексагона
В стране, где человеческий рост измеряют в футах, расстояние до соседнего города считают в милях, а топливо в бак льют галлонами, чиновники выписывают справки на бумаге формата Letter. Американский «официальный» лист короче привычного международного А4 на 18 мм. Если бы не эта разница, возможно, мы бы до сих пор не знали о флексагонах — увлекательной игрушке, головоломке и интересной математической модели, открытой в первой половине XX века.
В конце 1939 года Артур Стоун, 23 летний аспирант из Англии, изучавший математику в Принстоне, обрезал листы американского блокнота, чтобы подогнать их под привычный формат. Желая немного развлечься, Стоун принялся складывать из отрезанных полосок бумаги различные фигуры. Одна из сделанных им фигур оказалась особенной интересной. Перегнув полоску бумаги в трех местах и соединив концы, он получил правильный шестиугольник. Взяв этот шестиугольник за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что, когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были бы разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Так был открыт самый первый флексагон с тремя поверхностями. Поразмыслив над ним ночь, Стоун наутро убедился в правильности своих чисто умозрительных заключений: оказалось, можно построить и более сложный шестиугольник с шестью поверхностями вместо трех. Эта модель показалась Стоуну настолько интересной, что он решил показать её своим друзьям по университету. Вскоре был создан «Флексагонный комитет», куда вошли сам Стоун, аспирант-математик Бриан Таккерман, аспирант-физик Ричард Фейнман и молодой преподаватель математики Джон У.Тьюки. Комитет обнаружил, что можно сделать флексагоны с 9, 12, 15 и большим числом поверхностей. Таккерману удалось сделать действующую модель флексагона с 48 поверхностями. Он также обнаружил, что из зигзагообразной полоски бумаги можно сложить тетрагексафлексагон (с четырьмя) и пентагексафлексагон (с пятью поверхностями). Вообще один вид флексагона можно складывать по-разному. Так, гексагексафлексагон можно сложить тремя способами, а декагексафлексагон - 82 способами.
Тетрафлексагоны были открыты на несколько столетий раньше гексафлексагонов, однако они гораздо менее изучены. Артур Стоун с друзьями посвятили много времени складыванию этих четырёхсторонних разновидностей флексагонов, но им так и не удалось построить полную теорию, охватывающую все, на первый взгляд ничем не связанные, разновидности этих головоломок. Конструкция тетрафлексагонов используется в шарнирных соединениях «двойного действия» – устройствах, с одинаковой лёгкостью открывающихся в обе стороны. Эту же конструкцию можно обнаружить и в детских игрушках. Также флексагоны натолкнули на идею создания фильма и т.д.
След в истории 7 декабря 1941 года японцы ворвались в Перл-Харбор, и война разбросала участников «Флексагонного комитета» по свету. Впоследствии Артур Стоун приобрел всемирную известность как специалист в области топологии и автор теоремы метризации, названной в его честь. Джон Тьюки получил титул магистра химии и докторскую степень по математике. Он изобрел несколько основополагающих методов современной статистики. Брайант Таккерман оставил значительный след в информатике как один из соавторов симметричного алгоритма защиты информации, в котором один ключ используется как для шифрования, так и для расшифровки данных. А Ричард Фейнман и вовсе не нуждается в представлении как обладатель премии Альберта Эйнштейна и Нобелевской премии в области физики. Долгие годы эти блестящие ученые хотели вновь собраться вместе, чтобы написать пару статей и покончить со всеми тайнами теории флексагонов. К сожалению, или, напротив, к счастью, этому плану не суждено было сбыться.
Виды флексагонов и их классификация
Флексагоны - это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной, изогнутой формы, которые обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а ранее скрытые поверхности неожиданно выходят наружу. Происходит это слово от английского toflex, что означает «складываться, гнуться».
Флексагоны бывают следующих видов:
Унагексафлексагон.
Дуогексафлексагон.
Тригексафлексагон.
Тетрагексафлексагон.
Пентагексафлексагон.
Гексагексафлексагон.
Гептагексафлексагон.
Тетрафлексагоны
Человек незнакомый с флексагонами будет удивлен, увидев следующие названия: дотриаконтагектагексафлексагон, дотриаконтагектатетрафлексагон.
Разобраться в этих названиях на самом деле не сложно, каждое название состоит из трех частей: двух приставок и слова «флексагон». Первая приставка показывает порядок флексагона (число чередующихся поверхностей), вторая определяет форму флексагона. Приставки образуются из корней греческих и латинских числительных, применяемых для обозначений соединений по правилам номенклатуры органических соединений. Примеры таких приставок приведены ниже (Таблица 1).
| Число | приставка |
|
| Число | приставка |
| Число | приставка |
|
|
|
|
|
|
|
|
|
| 2 | ди- или би- |
| 15 | пентадека- |
| 29 | нонакоса |
|
| три- |
|
| 16 | гексадека- |
| 30 | триаконта- |
| 3 |
|
|
|
| 4 | тетра- |
|
| 17 | гептадека- |
| 31 | гентриаконта |
|
| пента- |
|
| 18 | октадека- |
| 40 | тетраконта- |
| 5 |
|
|
|
| 6 | гекса- |
|
| 19 | нонадека- |
| 41 | гентетракон- |
|
|
|
|
|
|
|
|
| та- |
| 7 | гепта- |
|
| 20 | эйкоси- (эй- |
|
|
| 8 | окта- |
|
|
| коса-) |
| 50 | пентаконта |
|
|
|
|
|
|
| эннеа- | или |
| 21 | генэйкоса |
| 60 | гексаконта |
| 9 |
|
|
|
| нона |
|
| 22 | докоса |
| 70 | гептаконта- |
| 10 | дека- |
|
| 23 | трикоса |
| 80 | октаконта- |
|
| ундека- (ген- |
| 24 | тетракоса- |
| 90 | эннеаконта |
| 11 |
|
|
|
| дека-) |
|
| 25 | пентакоса |
| 100 | гекта |
| 12 | додека- |
|
| 26 | гексакоса |
| 132 | дотриаконта- |
|
| тридека |
|
| 27 | гептакоса |
|
| гекта |
| 13 |
|
|
|
|
| 14 | тетрадека- |
|
|
|
|
|
|
|
|
|
| 28 | октакоса |
|
|
|
Таблица1
Установим, о каких двух флексагонах идет речь в нашем случае.
По таблице определяем, что в слове дотриаконтагектагексафлексагон первая приставка «дотриаконтагекта», вторая – «гекса»:

д о т р и а к о н т а г е к т а г е к с а ф л е к с а г о н
З начит, мы имеем дело с флексагоном, состоящим из 132 поверхностей, в форме шестиугольника (рис. 1).
начит, мы имеем дело с флексагоном, состоящим из 132 поверхностей, в форме шестиугольника (рис. 1).
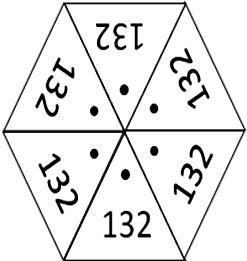
Рис.1. Дотриаконтагектагексафлексагон
Аналогично разбираемся со вторым названием: дотриаконтагектатетрафлексагон:

д о т р и а к о н т а г е к т а т е т р а ф л е к с а г о н
о т р и а к о н т а г е к т а т е т р а ф л е к с а г о н
Первая приставка та же, т.е. поверхностей 132, вторая приставка говорит о том, что флексагон имеет форму четырехугольника (Рис. 2).
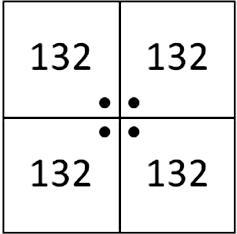
Рис.2. Дотриаконтагектатетрафлексагон
Первая созданная Артуром Стоуном фигура – тригексафлексагон, т.е. она состояла из трех поверхностей и имела форму шестиугольника.
Применение флексагонов
Флексагоны и флексоры могут быть основой творчества. Например, известно, что, когда изобретатель флексагонов Артур Х. Стоун и его друзья создали и исследовали игрушку, они попутно придумали историю об одном джентельмене, у которого в флексагон попал кончик галстука. Порвать любовно сделанную игрушку, было жаль, и он продолжал играть, напрасно надеясь, что при очередном перегибании удастся освободиться. Эта сочиненная история легла в сюжет любительского фильма «Осторожно, математика!»
Изучив флексагоны, мы смогли убедиться, что их можно использовать не только как интересные геометрические головоломки, но и найти им много других применений:
Если каждый треугольник гексафлексагона раскрасить в свой цвет, то можно применять его для изучения цветов у детей дошкольного возраста. На каждом треугольнике можно поместить не только цвета, но и геометрические фигуры, рисунки животных, деревьев, цветов и др. На одном тригексафлексагоне разместятся 18 предметов одного вида, а на гексагексафлексагоне – 36. Таким образом, флексагон станет для ребенка не только забавной игрушкой, которую можно выворачивать, но и наглядным обучающим материалом.
Флексагоны можно применять на уроках математики, если на их сторонах написать числа и знаки «+», «-», «×», «:». Выворачивая флексагон, можно числа складывать, вычитать, умножать и делить. Правда, при вычитании может получиться отрицательное число, а при делении – не всегда получится целое.
Необычно применение флексагона в качестве шпаргалки. Написав на его сторонах формулы или правила, можно вывернуть флексагон обычными раскрашенными сторонами наружу. Такой полезный флексагон вешается на шею, как кулон, а в нужный момент разворачивается. Есть только опасность, что до нужной подсказки придется очень долго добираться, ведь известно, что 1, 2 и 3 стороны открываются в три раза чаще, чем 4, 5 и 6.
Флексагон можно использовать в качестве фоторамки. На все треугольники приклеиваются фотографии (например, друзей). Такой фоторамке не требуется специальная подставка.
Флексагоны можно подарить друзьям в качестве сувенира или во время проведения праздника научить их делать эти геометрические игрушки.
Простейшие флексагоны, раскрашенные в разные цвета или сделанные из фольги, можно использовать в качестве елочных украшений или обычного оформления праздника.
Глава 2. Практические аспекты исследования
2.1 Конструирование флексагонов
2.1.1 Тригексафлексагон
Тригексафлексагон можно сконструировать за 4 шага.
ШАГ 1
Подготовить изображенную ниже полоску бумаги (можно изобразить на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на треугольники, в обе стороны, чтобы будущий флексагон легко разворачивался.


ШАГ 2
Правую часть согнуть назад

ШАГ 3
В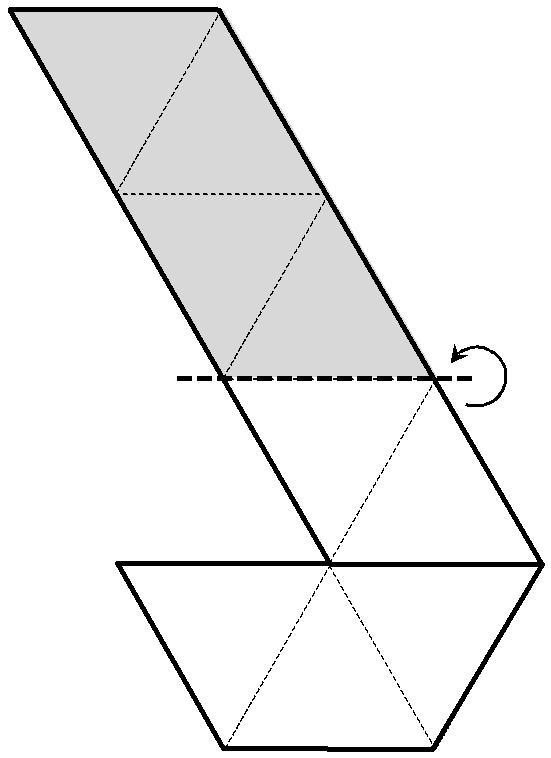 ерхнюю часть согнуть назад положить на треугольник 1
ерхнюю часть согнуть назад положить на треугольник 1
ШАГ4
Л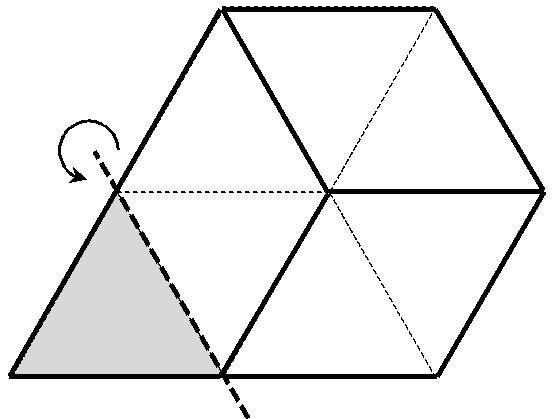 евую часть согнуть назад и наклеить на треугольник 1 с обратной стороны.
евую часть согнуть назад и наклеить на треугольник 1 с обратной стороны.
2.1.2 Гексагексафлексагон
Конструирование гексагексафлексагона можно разбить на 4 шага.
ШАГ 1
 Подготовить изображенную ниже полоску бумаги так, как это описано выше
Подготовить изображенную ниже полоску бумаги так, как это описано выше
ШАГ 2
Пронумеровать треугольники с одной стороны:
|
| 2 | 1 | 3 | 2 | 1 | 3 | 2 | 1 | 3 |
| 1 | 3 | 2 | 1 |
| 3 | 2 | 1 | 3 | 2 |

Перевернуть эту полоску сверху вниз и пронумеровать треугольники с другой стороны:

| 4 | 5 | 6 | 4 |
| 5 | 6 | 4 | 5 | 6 |
| 4 | 5 | 6 | 4 | 5 | 6 |
| 4 | 5 | 6 |
ШАГ 3
Сложить полоску так, чтобы треугольники с обратной стороны, имеющие одинаковые номера, оказались наложенными друг на друга. В результате получится следующая полоска.
|  1 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 1 | 2 | 3 |
ШАГ 4
Далее с этой полоской работаем по схеме сборки тригексафлексагона. Склеенными окажутся непронумерованные стороны двух треугольников.
2.2.3 Тритетрафлексагон
Тритетрафлексагон можно собрать за 6 шагов.
| ШАГ 1 | Подготовить изображенную ниже фигуру из бумаги (можно изобразить ![]() ![]() на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался: на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался: 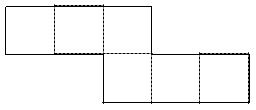
| |
|
|
|
|
| ШАГ 2 Пронумеровать с одной стороны:
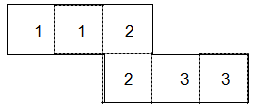
|
| ШАГ 3 П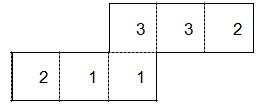 еревернуть заготовку с лева на право и пронумеровать с другой стороны: еревернуть заготовку с лева на право и пронумеровать с другой стороны:
| ШАГ 4 Л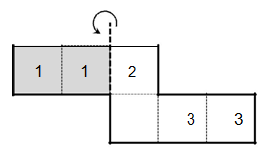 евую часть согнуть назад: евую часть согнуть назад:
|
| ШАГ 5 П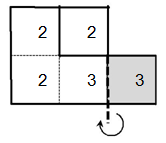 равую часть согнуть вперед (тройку наложить на тройку) равую часть согнуть вперед (тройку наложить на тройку)
| ШАГ 6 Наклеить прозрачную ленту: 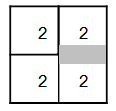
|
2.2.4 Тетратетрафлексагон
Тритетрафлексагон можно собрать за 9 шагов.
| ШАГ 1 П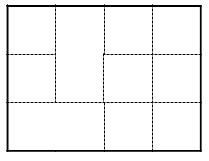 одготовить изображенную ниже фигуру из бумаги (можно изобразить на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался одготовить изображенную ниже фигуру из бумаги (можно изобразить на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался
| ШАГ 2 П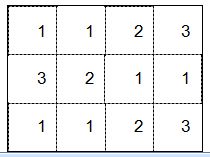 ронумеровать с одной стороны: ронумеровать с одной стороны:
|
| ШАГ 3 Перевернуть заготовку слева направо и пронумеровать с другой стороны:
| ШАГ 4 Снова перевернуть заготовку слева направо и сделать такой разрез:
|
| ШАГ 5 Вырезанную часть согнуть по пунктирной линии и отвернуть назад влево:
| ШАГ 6 Правую часть согнуть назад:
|
| ШАГ 7 Правую часть согнуть назад:
| ШАГ 8 Левую часть согнуть вперед (тройку наложить на тройку):
|
| ШАГ 9 Н аклеить прозрачную ленту: аклеить прозрачную ленту:
|
|
2.1.5 Гексатетрафлексагон
Процесс сборки гексатетрафлексагона можно разбить на 13 шагов.
| ШАГ 1 П одготовить изображенную ниже фигуру (можно изобразить на компьютере и распечатать), прогнуть каждую линию, разделяющую полоску на квадраты в обе стороны, чтобы будущий флексагон легко разворачивался: одготовить изображенную ниже фигуру (можно изобразить на компьютере и распечатать), прогнуть каждую линию, разделяющую полоску на квадраты в обе стороны, чтобы будущий флексагон легко разворачивался:
| ШАГ 2 Пронумеровать с одной стороны:
|
|
ШАГ 3 Перевернуть заготовку слева на права и пронумеровать с другой стороны:
|
ШАГ 4 Снова перевернуть заготовку слева на право и сделать такой разрез:
|
| ШАГ 5 Любую часть согнуть вперед (шесть наложить на шесть): | ШАГ 6 Верхнюю часть согнуть вперед (четверку совместить с четверкой): |
| ШАГ 7 Нижнюю часть согнуть назад: | ШАГ 8 Закрашенную часть загнуть назад: |
| ШАГ 9 Закрашенную часть загнуть назад: | ШАГ 10 Закрашенную часть согнуть вперед (шестерку наложить на шестерку): |
| ШАГ 11 Закрашенную часть согнуть вперед (наложить пятерку на пятерку): | ШАГ 12 Закрашенный квадрат завернуть под расположенный за ним квадрат: В итоге тройки окажутся наложенными друг на друга, и расположенная за закрашенным квадратом двойка окажется наверху:
|
| ШАГ 13 Наклеить прозрачную ленту на левый верхний квадрат, как показано на рисунке, завернуть ее и наклеить на обратную сторону:
|
|
2.2 Разворачивание флексагонов
Флексагоны разворачиваются по-разному. Чтобы развернуть гексафлексагон, нужно одной рукой взять за два соседних треугольника, примыкающих к какой-нибудь вершине фигуры, а другой рукой потянуть за свободный край двух противоположных треугольников. При открывании такой флексагон выворачивается наизнанку, и наружу выходит поверхность, которая ранее скрывалась внутри (рис. 3).
Чтобы развернуть тетрафлексагон, нужно перегнуть его по вертикальной или горизонтальной оси и вывернуть с места перегиба.
Рис.3. Разворачивание тетрафлексагона
Иногда бывает сложно увидеть какую-то поверхность флексагона, разворачивая флексагон мы постоянно видим одни и те же поверхности, а другие поверхности прячутся где-то внутри. С этой проблемой справился Льюис Таккерман. Оказывается, чтобы выявить все поверхности любого флексагона, держа за какой-нибудь угол, следует открывать фигуру до тех пор, пока это возможно, а затем переходить к следующему углу.
Если пронумеровать поверхности флексагон, то, пользуясь описанным правилом, можно построить схему, демонстрирующую переходы от одной поверхности флексагона к другой. Эта схема представляет собой ориентированный граф, вершинам которого соответствуют номера поверхностей флексагона, а дуги указывают, в каком порядке становятся видимыми поверхности флексагона. Такие графы называются путями Таккермана.
На рисунке 4 представлен путь Таккермана для гегсагексафлексагона.
Рис.4. Путь Таккермана для гегсагексафлексагона
Заключение
Флексагон – это математическая головоломка. Очень увлекательная, забавная игрушка, обладающая удивительными свойствами. Флексагоны не так уж и распространены в современной науке и технике. Но даже такие объекты как флексагоны, причем всех разновидностей нашли свое применение в некоторых художественных областях. Флексагоны выступают в роли игрушек и головоломок. Действительно, бывает иногда занимательно складывать флексагоны, выворачивать их, наблюдать, как они меняют форму и поворачиваются к нам разными комбинациями сторон. Используются как открытки на различные темы.
Подводя итог по данной работе, хочется отметить, что поставленные цели и задачи были выполнены. Проведен анализ имеющейся информации о флексагонах. Освоены методики сложения флексагонов. Найдены примеры практического применения флексагонов.
В дальнейшем планируется более глубокое изучение данной области и создание новых моделей флексагонов.
Список используемой литературы
Афонькин С. Игры и фокусы с бумагой / С. Афонькин, Е. Афонькина. — М.: Рольф, АКИМ, 1999. — С. 12–67.
Белошистая А.В. Формирование и развитие математических способностей дошкольников: Вопросы теории и практики: Курс лекций. — М.: ВЛАДОС, 2003. — С. 11–77.
Игры и развлечения: Кн. 3 / Сост. Л.М. Фирсова. — М.: Мол. Гвардия, 1991.
Мартин Гарднер Математические головоломки и развлечения = MathematicalPuzzlesandDiversions / Пер. Ю. А. Данилова, под ред. Я. А. Смородинского. — 2-е. — М: Мир, 1999. — ISBN 5-03-003340-8
Статьи
1. А.А. Панов. Флексагоны. Флексоры. Флексманы. Ж. «Квант». – М.: «Бюро Квантум», 1988. № 7, C. 10 - 14
2. И. Кан. Треугольные флексагоны. Ж. «Наука и жизнь». – М.: «Пресса», 1993. №12, С. 42 – 43.











 ерхнюю часть согнуть назад положить на треугольник 1
ерхнюю часть согнуть назад положить на треугольник 1 евую часть согнуть назад и наклеить на треугольник 1 с обратной стороны.
евую часть согнуть назад и наклеить на треугольник 1 с обратной стороны. Подготовить изображенную ниже полоску бумаги так, как это описано выше
Подготовить изображенную ниже полоску бумаги так, как это описано выше

 1
1

 еревернуть заготовку с лева на право и пронумеровать с другой стороны:
еревернуть заготовку с лева на право и пронумеровать с другой стороны: евую часть согнуть назад:
евую часть согнуть назад: равую часть согнуть вперед (тройку наложить на тройку)
равую часть согнуть вперед (тройку наложить на тройку)
 одготовить изображенную ниже фигуру из бумаги (можно изобразить на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался
одготовить изображенную ниже фигуру из бумаги (можно изобразить на компьютере и распечатать). Прогнуть каждую линию, разделяющую полоску на квадраты, в обе стороны, чтобы будущий флексагон легко разворачивался ронумеровать с одной стороны:
ронумеровать с одной стороны:








Математика 5 класс
Электронная тетрадь по геометрии 7...
Алгебра 10 класс ФГОС
Электронная тетрадь по алгебре 8 класс...
Математика. Вероятность и статистика. 7...
Электронная тетрадь по математике 5...
Математика 5 класс ФГОС
Наглядная геометрия 5-6 классы ФГОС
© 2018, Борисова Анна Николаевна 2457 41
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы