Сечения круглых тел.

Сечения круглых тел.

Автор: Могилёва Т. Н., Зам. директора по УВР, учитель математики МОУ «СОШ №65 им.Б.П.Агапитова УИПМЭЦ» г.Магнитогорска

Введение

Еще в древности сечения тел вращения вызывали большой интерес. Ученые стремились как можно лучше изучить эту область.

В наши дни сечения круглых тел широко используются в науке, технике, быту. Поэтому важно развивать знания в этой области для дальнейших усовершенствований жизни.

История

Термины и понятия, связанные с телами вращения и их сечениями, пришли в нашу речь из латинского и греческого языков:

• конус – греч. « κώνος» - конус, сосновая шишка, остроконечная верхушка шлема; цилиндр – греч. « κύλινδρος» - свиток папируса, валик, каток; шар - лат. «sphaera» - сфера, шар, ком, диск.
• конус – греч. « κώνος» - конус, сосновая шишка, остроконечная верхушка шлема;
• цилиндр – греч. « κύλινδρος» - свиток папируса, валик, каток;
• шар - лат. «sphaera» - сфера, шар, ком, диск.

Сечения некоторых круглых тел были известны уже математикам Древней Греции. Например, конические сечения. Они встречаются нам в сочинениях Аполлония Пергского «Конические сечения». Именно он присвоил названия отдельным типам этих кривых:

слово «парабола» (греч. parabole) означает приложение;

• слово «парабола» (греч. parabole) означает приложение;
• слово «парабола» (греч. parabole) означает приложение;

«эллипс» (греч. elleipsis) – недостаток (приложение с недостатком);

«гипербола» (греч. hyperbole) – избыток (приложение с избытком).

• «эллипс» (греч. elleipsis) – недостаток (приложение с недостатком); «гипербола» (греч. hyperbole) – избыток (приложение с избытком).
• «эллипс» (греч. elleipsis) – недостаток (приложение с недостатком); «гипербола» (греч. hyperbole) – избыток (приложение с избытком).

Тела вращения

Прямым круговым цилиндром (рис. 1) называется фигура, полученная при вращении прямоугольника вокруг оси, проходящей через одну из его сторон.

О

R

S

Рис.1

Сферой называется множество точек пространства, удаленных от данной точки на заданное положительное расстояние.

Шаром (рис. 2) называется множество точек пространства, находящихся от данной точки на расстоянии, не большем некоторого данного положительного расстояния.

R

О

Рис. 2

Конической поверхностью называется поверхность, образованная движением прямой, которая проходит через данную точку и пересекает данную плоскую линию.

Конусом (рис. 3) называется тело, ограниченное замкнутой конической поверхностью и пересекающей ее плоскостью.

h

Рис. 3

Часть конуса, заключенная между основанием и плоскостью, параллельной основанию, называется усеченным конусом (рис. 4) .

h

Рис. 4

Методы построения сечений

Выделяют три способа построения сечений:

• метод следа;
• метод вспомогательных плоскостей;
• метод с использованием аксиом и теорем стереометрии.

След - линия пересечения секущей плоскости с плоскостью проекций. След секущей плоскости – прямая линия, поэтому для построения его изображения достаточно построить изображение двух его точек, каждая из которых есть пересечение некоторой прямой секущей плоскости с ее проекцией.

При использовании метода вспомогательных плоскостей для построения каждой точки рассматривают две вспомогательные плоскости, обладающие свойствами:

• первая плоскость проходит через две известные точки секущей плоскости и параллельно образующим (если это цилиндр) , либо через вершину (если конус); вторая проходит через третью известную точку секущей плоскости и образующие.
• первая плоскость проходит через две известные точки секущей плоскости и параллельно образующим (если это цилиндр) , либо через вершину (если конус);
• вторая проходит через третью известную точку секущей плоскости и образующие.

Сечение прямого кругового цилиндра

Если секущая плоскость перпендикулярна оси вращения (параллельна плоскости основания), в сечении прямого кругового цилиндра (рис. 5) получится окружность .

Рис. 5

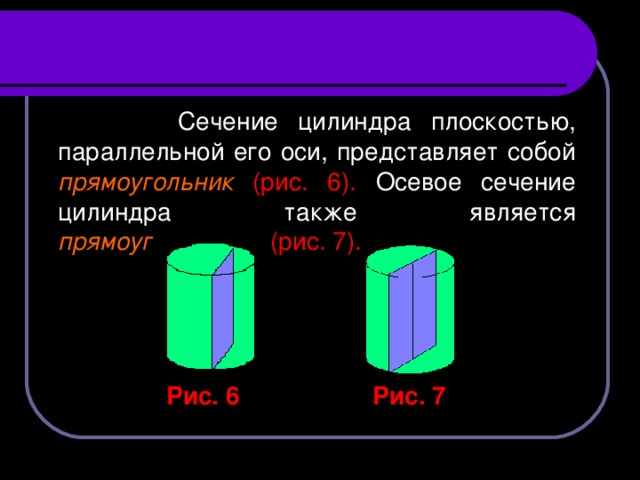
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 6). Осевое сечение цилиндра также является прямоугольником (рис. 7).

Рис. 6

Рис. 7

Относительно сечений цилиндра плоскостью можно вывести следующее:

• если секущая плоскость параллельна образующим цилиндра, то в сечении получается прямоугольник ;
• если секущая плоскость перпендикулярна к оси цилиндра, то сечение – окружность ;
• если секущая плоскость не перпендикулярна к оси и не параллельна образующим цилиндра, то в сечении будет эллипс .

Конические сечения

Плоские кривые линии, получаемые при пересечении поверхности прямого кругового конуса плоскостями, различно расположенными по отношению к оси конуса, называют кривыми конических сечений .

В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть (рис. 8) : эллипс , парабола , гипербола , а в частных случаях: окружность , прямая, две пересекающиеся прямые и точка.

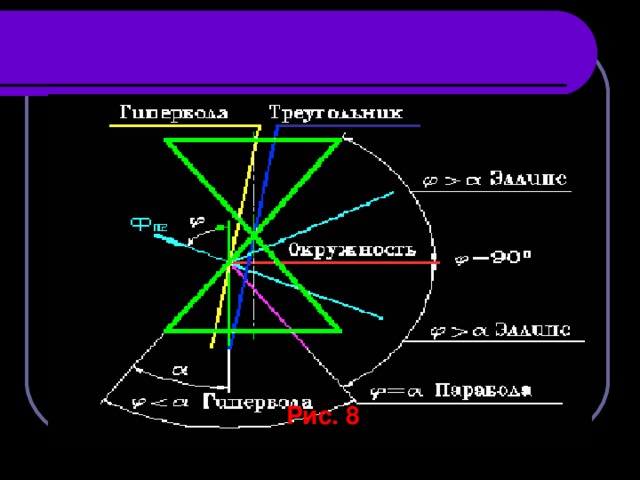
Рис. 8

Парабола (греч. parabole) - кривая второго порядка. Прямая пересекает ее не более чем в двух точках.

При этом парабола может быть определена как множество точек М(x y ) плоскости, расстояние FM которых до определенной точки F этой плоскости равно расстоянию MN до определенной прямой AN – директрисы параболы (рис. 9) .

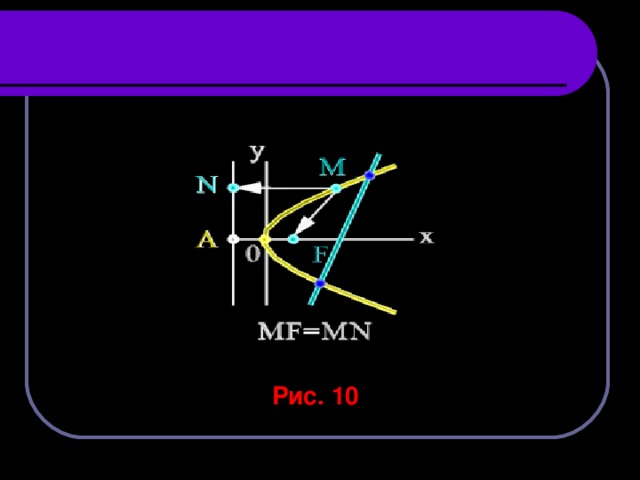
Рис. 10

Гипербола (греч. hyperbole) – плоская кривая линия (рис. 11). Гипербола – множество точек М плоскости, разность (по абсолютной величине) расстояний F1M и F2M которых до двух определенных точек F1 и F2 этой плоскости постоянна:

F1M – F2M = 2a .

Рис. 11

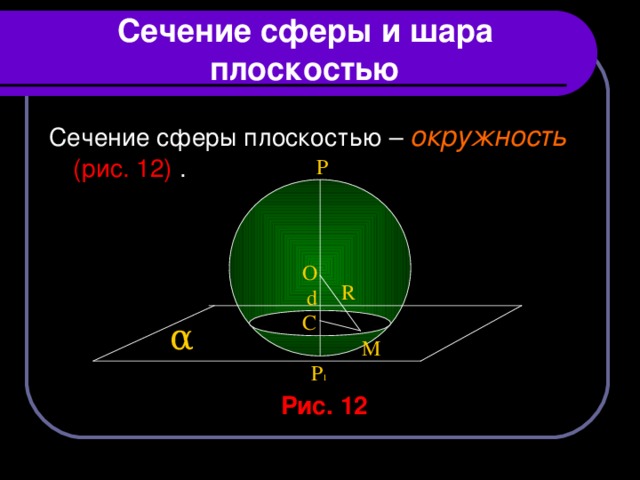
Сечение сферы и шара плоскостью

Сечение сферы плоскостью – окружность (рис. 12) .

Р

О

R

d

С

α

М

Р 1

Рис. 12

1 º Сечение шара плоскостью – круг .

2º Сечения шара плоскостями, равноудаленными от его центра, равны.

3º Сечение шара тем больше, чем оно ближе расположено к центру.

4º Два больших круга пересекаются по диаметру (рис. 13) .

Р

α

β

А

В

Р 1

Рис. 13

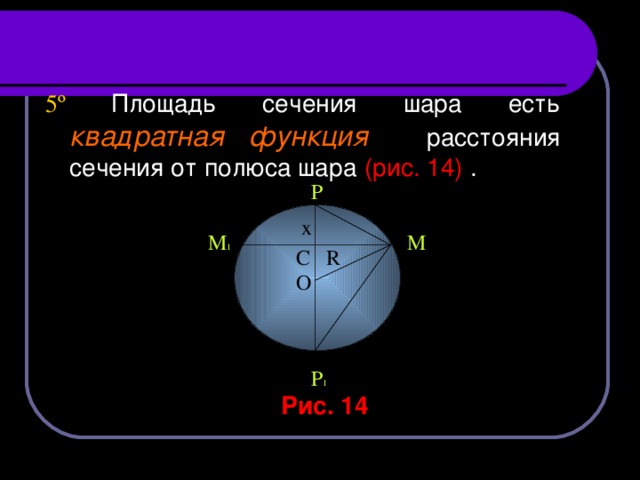
5 º Площадь сечения шара есть квадратная функция расстояния сечения от полюса шара (рис. 14) .

Р

x

М 1

М

R

C

О

Р 1

Рис. 14

Задачи

• Построить сечение цилиндра по трем точкам на боковой поверхности.
• Построить сечение конуса по трем точкам на боковой поверхности.

3) Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга? (рис. 15)

R/2

А

R

О

Рис. 15

Заключение

В нашей жизни стремительно развивается наука и техника, поэтому особенно важно изучить уже известные факты и моменты, связанные с сечениями круглых тел, на основе которых будут строиться дальнейшие разработки.