Семина Лилия Анатольевна
МКОУ «Средняя общеобразовательная школа д. Шибково»
Искитимского района Новосибирской области
2016 – 2017 уч. год
Семинар «Логарифмы»
Доклады учащихся.
Из истории логарифмов.
Открытие логарифмов было связано, в первую очередь, с быстрым развитием астрономии в XVI в., с уточнением астрономических наблюдений и усложнением астрономических выкладок. Авторы новых таблиц логарифмов исходили из зависимости между свойствами геометрической прогрессии и составляющих из показателей степеней членов арифметической прогрессии. Эти зависимости были частично подмечены еще Архимедом, хорошо известны Шюке и Штирелю. Логарифмы были введены шотландским математиком Дж. Непером (1550-1617) и независимо от него швейцарским механиком и математиком И. Бюрги (1552-1632). Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (1620).
При помощи приемов, по существу равносильных интегрированию некоторых простых дифференциальных уравнений, Непер вывел основные свойства логарифмов и вычислил обширные таблицы (1614г.). Таблицы Непера содержали 8-значные логарифмы синусов, косинусов и тангенсов для углов от 0° до 90° следующих через 1 минуту. Т.к. sin90° тогда принимали равным 107, а на него часто приходилось умножать, то Непер определил свои логарифмы таким образом, что логарифм 107 был равен 0. Логарифмы остальных синусов, меньших 107, у него положительны. Непер не ввел понятия об основании системы логарифмов. Его логарифм числа N в современных обозначениях  .
.
Свойства логарифмов Непера несколько сложнее обычных, т.к. у его логарифм 1 отличен от 0. Таблицы Бюрги представляли собой первую таблицу антилогарифмов («черные числа») и дают значения чисел, соответствующих равноотстоящим логарифмам («красным числам»). «Красные числа » Бюрги – суть логарифмов, поделенных на 108 «черных чисел» при основании, равном  .
.
«Арифметическая и геометрическая таблица прогрессий» (1620г., Бюрги) и особенно «Описание удивительной таблицы логарифмов » (1614г., Непер) немедленно привлекли внимание математиков к теории и вычислению логарифмов. По совету Непера английский математик Г.Бригс (1561-1630) вычислил 8-значные десятичные логарифмы (1617) от 1 до 1000; затем 14-значные (1624) от 1 до 20000 и от 90000 до 100000. (По его имени десятичные логарифмы иногда называли бриговыми). 10-значные таблицы от 1до 100000 издал голландский математик А.Влакк (1628). Таблицы Влакка легли в основу большинства последующих таблиц, причем дальнейшие авторы внесли много изменений в их структуру и поправок в выкладки: у самого Влакка было 173 ошибки, первые безошибочные таблицы выпустил в 1857г. немецкий математик К.Бреминер. В России таблицы логарифмов впервые были изданы в 1703 г. При участии Магницкого. Таблицы гауссовых логарифмов были опубликованы в 1802г. итальянским математиком Лионелли; немецкий математик К.Гаусс ввел (1812) эти логарифмы в общее употребление. Важный шаг в теоретическое изучение логарифмов сделал бельгийский математик Григорий из Сен-Винцента (1647), обнаруживший связь логарифмов и площадей, ограниченных дугой гиперболы, осью абсицсс и соответственно ординатами. Представление логарифмов бесконечным степенным рядом дано немецким ученым Меркаротом (1668), нашедшим что: Ln (1+x) =  -
- 
Математик Дж. Грегори (1668) открыл разложение

Этот ряд очень быстро сходится, если  достаточно велико; поэтому он может быть использован для вычисления логарифмов. В развитии теории логарифмов большое значение имели работы петербургского академика Л.Эйлера. Он впервые исследовал показательную и логарифмическую функции при комплексных значениях аргумента, открыл многозначность обобщенных логарифмов в комплексной области. Им же установлено понятие о логарифмировании, как действии, обратном возведению в степень. Термин «логарифмы» предложил Непер; он возник из сочетания греческих слов:
достаточно велико; поэтому он может быть использован для вычисления логарифмов. В развитии теории логарифмов большое значение имели работы петербургского академика Л.Эйлера. Он впервые исследовал показательную и логарифмическую функции при комплексных значениях аргумента, открыл многозначность обобщенных логарифмов в комплексной области. Им же установлено понятие о логарифмировании, как действии, обратном возведению в степень. Термин «логарифмы» предложил Непер; он возник из сочетания греческих слов:
λογος – «смысл, слово, отношение» и άqίθμό – «число». В античной математике отношения  называли «двойным», «тройным» и т.д. отношением. Таким образом, для Непера слова « λογος άqίθμό» – означали «число (кратность) отношения», т.е. логарифм у Непера – вспомогательное число для измерения отношения двух чисел (сначала он называл логарифмы искусственными числами). Термин «натуральный логарифм» принадлежал Меркатору, «характеристика» - Бригсу; «мантисса» в нашем смысле » - Эйлеру, «основание» логарифма – ему же. Понятие о модуле перехода ввел Меркатор. Современное определение логарифмов впервые дано В. Гардинерем (1712).Знак логарифма – результат сокращения слова «логарифм» - встречается в несколько различных видах почти одновременно с появлением первых таблиц:
называли «двойным», «тройным» и т.д. отношением. Таким образом, для Непера слова « λογος άqίθμό» – означали «число (кратность) отношения», т.е. логарифм у Непера – вспомогательное число для измерения отношения двух чисел (сначала он называл логарифмы искусственными числами). Термин «натуральный логарифм» принадлежал Меркатору, «характеристика» - Бригсу; «мантисса» в нашем смысле » - Эйлеру, «основание» логарифма – ему же. Понятие о модуле перехода ввел Меркатор. Современное определение логарифмов впервые дано В. Гардинерем (1712).Знак логарифма – результат сокращения слова «логарифм» - встречается в несколько различных видах почти одновременно с появлением первых таблиц:
log – у Кеплера (1624) и Бюрги (1631);
L – у немецкого математика Урсинуса (1624);
log и l – у итальянского математика Кавальери (1632, 1643).
Джон Непер
Джон Непер –шотландский математик, изобретатель логарифмов. Основными идеями учения о логарифмах непер овладел не позднее 1594 года, однако его «Описание удивительной таблицы логарифмов», в котором изложено это учение, было издано в 1614 году. В этом труде содержалось определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии. В «Построении удивительной таблицы логарифмов» Непер изложил принципы вычисления таблиц. Открытие Непера сыграло огромную роль в развитии математики и, в частности, в развитии техники вычислений. Кинематическое определение логарифма, данное Непером, и по существу равносильное определению логарифмической функции через дифференциальное уравнение, оказало значительное влияние на развитие исчисления бесконечно малых. Джону Неперу принадлежит также ряд удобных для логарифмирования формул решения сферических треугольников, среди них такие, например, неперовы аналогии. Непер был непримиримым противником католицизма; в труде «Ясное толкование всего откровения св. Иоанна» (1593), написанного в стиле геометрического трактата, он резко выступал против римского папы. Эта книга получила в XVII веке широкую известность, неоднократно издавалась на английском и других языках.
Таблицы логарифмов.
Логарифмические таблицы - таблицы, содержащие мантиссы (дробные положительные части) логарифмов положительных чисел. Логарифмические таблицы бывают и четырехзначные (содержат четыре знака мантиссы), и пятизначные, и большей значности.
Первые логарифмические таблицы были опубликованы Д.Непером в 1614 г. Его таблицы в связи со специальными целями содержали логарифмы тригонометрических функций по основанию e (основание натуральных логарифмов). В неперовских таблицах логарифм числа a равен  . Затем логарифмические таблицы, близкие к неперовым, издал швейцарский математик И. Бюрги (1620). В 1617 г. Бригс опубликовал таблицы десятичных логарифмов для натуральных чисел от 1 до 1000 с 14 знаками, а затем в 1624 г. он опубликовал также логарифмические таблицы с 14 знаками для чисел от 1 до 20000 и от 90000 до 100000.
. Затем логарифмические таблицы, близкие к неперовым, издал швейцарский математик И. Бюрги (1620). В 1617 г. Бригс опубликовал таблицы десятичных логарифмов для натуральных чисел от 1 до 1000 с 14 знаками, а затем в 1624 г. он опубликовал также логарифмические таблицы с 14 знаками для чисел от 1 до 20000 и от 90000 до 100000.
Голландский математик А. Влакк опубликовал (1628) второе издание таблиц Бригса, устраняя пробел чисел от 20000 до 90000,но уже не с 14 знаками, а только с 10 знаками; эти таблицы стали выпускать во многих странах мира. На русском языке первые логарифмические таблицы были изданы лишь в 1703 г., а затем в 1716г. для чисел от 1 до 10000 (Андрей Фархварсон, Леонтий Магницкий). Из многих логарифмических таблиц, издававшихся во многих странах, наибольшее распространение, очевидно, имели семизначные таблицы Г.Вега; эти логарифмическими таблицами используют и сейчас.
При основании, равном 10, только логарифм целых степеней числа 10 представляются целыми числами ( ), логарифмы же остальных чисел представляются дробями и в таблицах даются их приближенные значения в виде конечных десятичных дробей. Например,
), логарифмы же остальных чисел представляются дробями и в таблицах даются их приближенные значения в виде конечных десятичных дробей. Например,  Целая часть значений логарифма называется характеристикой, дробная – мантиссой. Любое положительное число N всегда можно представить в виде
Целая часть значений логарифма называется характеристикой, дробная – мантиссой. Любое положительное число N всегда можно представить в виде  , где n- целое число, а x заключено в пределах от 1 до 10. Заметим, что
, где n- целое число, а x заключено в пределах от 1 до 10. Заметим, что  а для любого числа х, заключенного между 1 и 10, его логарифм заключен между нулем и единицей:
а для любого числа х, заключенного между 1 и 10, его логарифм заключен между нулем и единицей:
 . Из этого представления числа N следует, что
. Из этого представления числа N следует, что  , где n – характеристика, а lg x - мантисса числа N.
, где n – характеристика, а lg x - мантисса числа N.
Характеристику числа определяют по его виду. Для числа, большего единицы, характеристика на единицу меньше числа цифр у целой части этого числа. Для числа, заключенного между нулем и единицей, и записанного десятичной дробью, характеристика отрицательна и равна взятому со знаком «минус» числу нулей до первой значащей цифры. Например, для числа 0,0216 его характеристика равна - 2. Благодаря такому простому способу определения характеристики в таблицах даются одни мантиссы.
Основанием таблицы логарифмов Непера является иррациональное число, к которому неограниченно приближаются числа вида  при безграничном возрастании n. Это число называют неперовым числом и со времен Л. Эйлера обозначают буквой е:
при безграничном возрастании n. Это число называют неперовым числом и со времен Л. Эйлера обозначают буквой е:  Непер составил таблицы, взяв очень хорошее приближение числа е, а именно
Непер составил таблицы, взяв очень хорошее приближение числа е, а именно  Логарифмы по основанию е называются натуральными логарифмами и обозначаются ln (образовано от первых букв слов «логарифм натуральный»).
Логарифмы по основанию е называются натуральными логарифмами и обозначаются ln (образовано от первых букв слов «логарифм натуральный»).
Логарифмическая линейка
Логарифмическая линейка – инструмент, служащий для выполнения разнообразных вычислений. С помощью линейки можно выполнять умножение, деление, извлечение корня, возведение в степень, тригонометрические вычисления, решение уравнений и т. д. Логарифмическая линейка состоит из корпуса с передвигающимся в нем движком и бегунка – рамки со стеклом, на котором отмечена визирная линия. На движке и корпусе логарифмической линейки нанесены логарифмические шкалы ( из них шкалы А и В, С и D тождественны), построены так, что расстояние штриха, помеченного числом n от начального штриха равно
 , где
, где  – так называемый модуль шкалы. Для шкал
– так называемый модуль шкалы. Для шкал  C и D в логарифмической линейке обычного размера
C и D в логарифмической линейке обычного размера  мм, а для шкал А и В
мм, а для шкал А и В  мм; шкалы А и В укладываются на протяжении шкалы Д два раза. Устанавливая начало или конец шкалы С движка против штриха m шкалы Д на корпусе металлической линейки, получают против штриха n шкалы С произведение mn на шкале Д. Частное
мм; шкалы А и В укладываются на протяжении шкалы Д два раза. Устанавливая начало или конец шкалы С движка против штриха m шкалы Д на корпусе металлической линейки, получают против штриха n шкалы С произведение mn на шкале Д. Частное  находят, совмещая штрихи m шкалы Д и n шкалы С; тогда начало или конец шкалы С указывает на шкале Д частное
находят, совмещая штрихи m шкалы Д и n шкалы С; тогда начало или конец шкалы С указывает на шкале Д частное  Шкалы А и В дают квадраты чисел шкал Д и С. Кроме этих основных шкал на лицевой стороне корпуса логарифмической линейки обычного типа имеются:
Шкалы А и В дают квадраты чисел шкал Д и С. Кроме этих основных шкал на лицевой стороне корпуса логарифмической линейки обычного типа имеются:
шкала К, дающая кубы чисел шкалы Д,
равномерная шкала L, дающая мантиссы логарифмов чисел шкалы Д,
на движке часто помещается шкала R, которая представляет собой нанесенную в обратном направлении (справа налево) шкалу Д; эта шкала дает обратные величины шкалы Д,
на обратной стороне движка помещены связанные со шкалой Д шкалы тригонометрических величин: синусов (S), тангенсов (Т), синусов и тангенсов малых углов (S&T).
Если движок вставить в корпус линейки обратной стороной, то на шкале Д можно прочесть значение тригонометрических функций углов, нанесенных на шкалах S, T, S&T. Кроме обыкновенной счетной (логарифмической) линейки, имеется большое число специальных счетных линеек, на которых нанесены шкалы, приспособленные для специальных расчетов (электротехнические, гидравлические и т.д.). Для вычислений, требующих точности большей, чем даваемая обыкновенной логарифмической линейкой, употребляется линейка с большим модулем  мм для шкал С и Д; эти линейки часто изготавливаются со шкалами, разрезанными на две части. Для увеличения модуля (с сохранением габаритов) логарифмическая линейка иногда изготавливается в виде дисков со шкалами на скользящих друг по другу спиралями и т.д. Выпускаются также маленькие (карманные) логарифмические линейки с модулем
мм для шкал С и Д; эти линейки часто изготавливаются со шкалами, разрезанными на две части. Для увеличения модуля (с сохранением габаритов) логарифмическая линейка иногда изготавливается в виде дисков со шкалами на скользящих друг по другу спиралями и т.д. Выпускаются также маленькие (карманные) логарифмические линейки с модулем  мм.
мм.
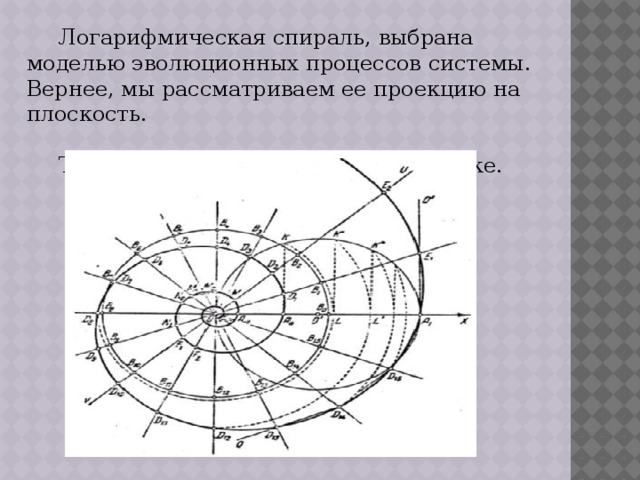
Логарифмическая спираль
Логарифмическая спираль - кривая, уравнение которой в полярных координатах имеет вид  Полюс является асимптотической точкой логарифмической спирали. Угол α между касательной к логарифмической спирали и радиус-вектором, проведенным в точку касания, постоянен ctg α = k. В силу этого логарифмическая спираль есть озогональная траектория пучка прямых, проходящих через полюс. Длина дуги логарифмической спирали, отсчитываемая от полюса пропорциональна ее радиус-вектору. Натуральной уравнение логарифмической спирали имеет вид
Полюс является асимптотической точкой логарифмической спирали. Угол α между касательной к логарифмической спирали и радиус-вектором, проведенным в точку касания, постоянен ctg α = k. В силу этого логарифмическая спираль есть озогональная траектория пучка прямых, проходящих через полюс. Длина дуги логарифмической спирали, отсчитываемая от полюса пропорциональна ее радиус-вектору. Натуральной уравнение логарифмической спирали имеет вид  Логарифмическая спираль является интегральной кривой дифференциального уравнения
Логарифмическая спираль является интегральной кривой дифференциального уравнения  Она была известна многим математикам XVII века, например, Р.Декарт, Э. Торричелли.
Она была известна многим математикам XVII века, например, Р.Декарт, Э. Торричелли.
Спираль эта имеет бесконечное множество витков и при раскручивании, и при скручивании. Последнее означает, что она не проходит через свой полюс. Логарифмическую спираль еще называют равноугольной спиралью.
Логарифмическая спираль часто используется в технических устройствах. Например, вращающиеся ножи нередко имеют профиль, очерченный по логарифмической спирали – под постоянным углом к разрезаемой поверхности, благодаря чему лезвие ножа стачивается равномерно. Ночные бабочки, которые пролетают большие расстояния, ориентируясь параллельным лунным лучам, инстинктивно сохраняют постоянный угол между направлением полета и лучом света. Если они ориентируются на точечный источник света, скажем на пламя свечи, инстинкт их подводит, и бабочки падают в пламя по скручивающейся логарифмической спирали.







 .
. .
. -
- 

 достаточно велико; поэтому он может быть использован для вычисления логарифмов. В развитии теории логарифмов большое значение имели работы петербургского академика Л.Эйлера. Он впервые исследовал показательную и логарифмическую функции при комплексных значениях аргумента, открыл многозначность обобщенных логарифмов в комплексной области. Им же установлено понятие о логарифмировании, как действии, обратном возведению в степень. Термин «логарифмы» предложил Непер; он возник из сочетания греческих слов:
достаточно велико; поэтому он может быть использован для вычисления логарифмов. В развитии теории логарифмов большое значение имели работы петербургского академика Л.Эйлера. Он впервые исследовал показательную и логарифмическую функции при комплексных значениях аргумента, открыл многозначность обобщенных логарифмов в комплексной области. Им же установлено понятие о логарифмировании, как действии, обратном возведению в степень. Термин «логарифмы» предложил Непер; он возник из сочетания греческих слов:  называли «двойным», «тройным» и т.д. отношением. Таким образом, для Непера слова « λ
называли «двойным», «тройным» и т.д. отношением. Таким образом, для Непера слова « λ . Затем логарифмические таблицы, близкие к неперовым, издал швейцарский математик И. Бюрги (1620). В 1617 г. Бригс опубликовал таблицы десятичных логарифмов для натуральных чисел от 1 до 1000 с 14 знаками, а затем в 1624 г. он опубликовал также логарифмические таблицы с 14 знаками для чисел от 1 до 20000 и от 90000 до 100000.
. Затем логарифмические таблицы, близкие к неперовым, издал швейцарский математик И. Бюрги (1620). В 1617 г. Бригс опубликовал таблицы десятичных логарифмов для натуральных чисел от 1 до 1000 с 14 знаками, а затем в 1624 г. он опубликовал также логарифмические таблицы с 14 знаками для чисел от 1 до 20000 и от 90000 до 100000. ), логарифмы же остальных чисел представляются дробями и в таблицах даются их приближенные значения в виде конечных десятичных дробей. Например,
), логарифмы же остальных чисел представляются дробями и в таблицах даются их приближенные значения в виде конечных десятичных дробей. Например,  Целая часть значений логарифма называется характеристикой, дробная – мантиссой. Любое положительное число
Целая часть значений логарифма называется характеристикой, дробная – мантиссой. Любое положительное число  , где
, где  а для любого числа х, заключенного между 1 и 10, его логарифм заключен между нулем и единицей:
а для любого числа х, заключенного между 1 и 10, его логарифм заключен между нулем и единицей: . Из этого представления числа
. Из этого представления числа  , где
, где  при безграничном возрастании
при безграничном возрастании  Непер составил таблицы, взяв очень хорошее приближение числа е, а именно
Непер составил таблицы, взяв очень хорошее приближение числа е, а именно  Логарифмы по основанию е называются натуральными логарифмами и обозначаются
Логарифмы по основанию е называются натуральными логарифмами и обозначаются 
 , где
, где  – так называемый модуль шкалы. Для шкал
– так называемый модуль шкалы. Для шкал 
 мм, а для шкал А и В
мм, а для шкал А и В  мм; шкалы А и В укладываются на протяжении шкалы Д два раза. Устанавливая начало или конец шкалы С движка против штриха
мм; шкалы А и В укладываются на протяжении шкалы Д два раза. Устанавливая начало или конец шкалы С движка против штриха  находят, совмещая штрихи
находят, совмещая штрихи  Шкалы А и В дают квадраты чисел шкал Д и С. Кроме этих основных шкал на лицевой стороне корпуса логарифмической линейки обычного типа имеются:
Шкалы А и В дают квадраты чисел шкал Д и С. Кроме этих основных шкал на лицевой стороне корпуса логарифмической линейки обычного типа имеются:  мм для шкал С и Д; эти линейки часто изготавливаются со шкалами, разрезанными на две части. Для увеличения модуля (с сохранением габаритов) логарифмическая линейка иногда изготавливается в виде дисков со шкалами на скользящих друг по другу спиралями и т.д. Выпускаются также маленькие (карманные) логарифмические линейки с модулем
мм для шкал С и Д; эти линейки часто изготавливаются со шкалами, разрезанными на две части. Для увеличения модуля (с сохранением габаритов) логарифмическая линейка иногда изготавливается в виде дисков со шкалами на скользящих друг по другу спиралями и т.д. Выпускаются также маленькие (карманные) логарифмические линейки с модулем  Полюс является асимптотической точкой логарифмической спирали. Угол α между касательной к логарифмической спирали и радиус-вектором, проведенным в точку касания, постоянен
Полюс является асимптотической точкой логарифмической спирали. Угол α между касательной к логарифмической спирали и радиус-вектором, проведенным в точку касания, постоянен  Логарифмическая спираль является интегральной кривой дифференциального уравнения
Логарифмическая спираль является интегральной кривой дифференциального уравнения  Она была известна многим математикам
Она была известна многим математикам  .
. ,
,
 ,
,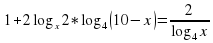 ,
, .
.
 ,
,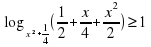 ,
,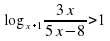 ,
, ,
,



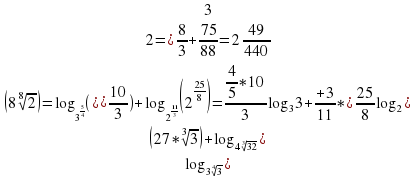
 ,
,


 т.к. функция
т.к. функция 
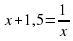



 ,
, ,
,




 ,
,


 ,
, , верно
, верно

 ;
; 
 , т.к. функция
, т.к. функция  монотонна, то
монотонна, то



 ОДЗ :
ОДЗ : 
 х – любое число
х – любое число

 ,
,
 ОДЗ:
ОДЗ: 







 .
. , где
, где  - скорость вылетающих газов,
- скорость вылетающих газов,  т.е. почти всю стартовую массу отдать под топливо.
т.е. почти всю стартовую массу отдать под топливо. , гдер0- давление звука до поглощения, р- давление звука, прошедшего через стену, А- некоторая
, гдер0- давление звука до поглощения, р- давление звука, прошедшего через стену, А- некоторая  т.е. стена снижает давление звука в 10 раз (такую изоляцию имеет деревянная дверь).
т.е. стена снижает давление звука в 10 раз (такую изоляцию имеет деревянная дверь).