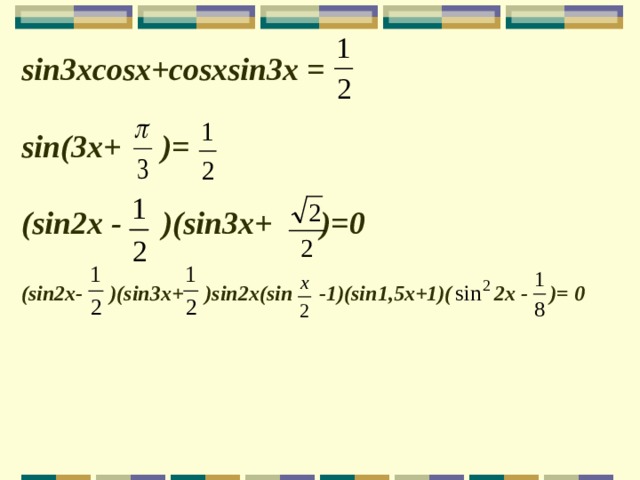Система простейших тригонометрических уравнений

Система простейших тригонометрических уравнений

УМК по алгебре и началам математического анализа С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин § 7. Синус и косинус угла- 7 ч § 8. Тангенс и котангенс угла- 4 ч § 9. Формулы сложения- 7 ч §10. Тригонометрические функции числового аргумента- 5 ч §11. Тригонометрические уравнения и неравенства- 5 ч

Новые дидактические компоненты:

• До сих пор при решении уравнений школьникам встречался лишь случай конечного множества корней. Теперь же уравнение имеет бесконечно много корней. Надо это воспринять и прочувствовать.
• Странный (для школьников) «хвост» в записи корней: то π n , то 2 π n ; более того, само наличие параметра n уже должно насторожить и учителя, и ученика. Мы же вместо осмысления ситуации заставляем детей просто писать каждый раз n Є Ζ . «Это, кстати, не соответствует четкости и организованности математиков, которые, как правило, о чем-то договариваются раз и навсегда и обычно соблюдают эту договоренность. Так вот, математики договорились, что в записи корней простейшего тригонометрического уравнения параметр n всегда принимает любые целочисленные значения, и практически никогда этого явно не пишут (за исключением особо ответственных случаев – на экзаменах или контрольных работах)»

3. Требуют специального внимания входящие в состав формул корней обратные тригонометрические функции – это тоже отдельный дидактический компонент.

4. Привыкнуть надо и к «выкрутасам» типа – это для учащихся далеко не просто.

5. Научив школьников решать уравнения вида sinx=a, cosx=a учитель может заметить, как тяжело им даются уравнения вида sin3x=a или

cos ( 2 x+ π/4 ) =a.

6. Весьма трудным в методическом плане является вопрос об отборе корней в тригонометрических уравнениях. В основном, отбору корней учат только в конце изучения раздела, посвященного тригонометрическим уравнениям. Это – методическая ошибка. Учить отбору корней надо именно на простейших уравнениях, заложив соответствующие сюжеты в систему упражнений. Задачи, связанные с отбором корней, просто бесценны для осознания структуры формулы корней, для понимания роли параметра в этой формуле. При этом полезно показать школьникам оба известных приема: перебор по параметру и решение двойного неравенства.

Чтобы успешно решать простейшие

тригонометрические уравнения нужно

1) уметь отмечать точки на числовой

окружности ;

2) уметь определять значения синуса, косинуса,

тангенса и котангенса для точек числовой

окружности ;

3) знать свойства основных

тригонометрических функций ;

4) знать понятие арксинуса, арккосинуса,

арктангенса, арккотангенса и уметь отмечать

их на числовой окружности.

20.11.19

Уравнения вида f ( x ) = а , где а – данное число, а f ( x ) – одна из тригонометрических функций, называют простейшими тригонометрическими уравнениями

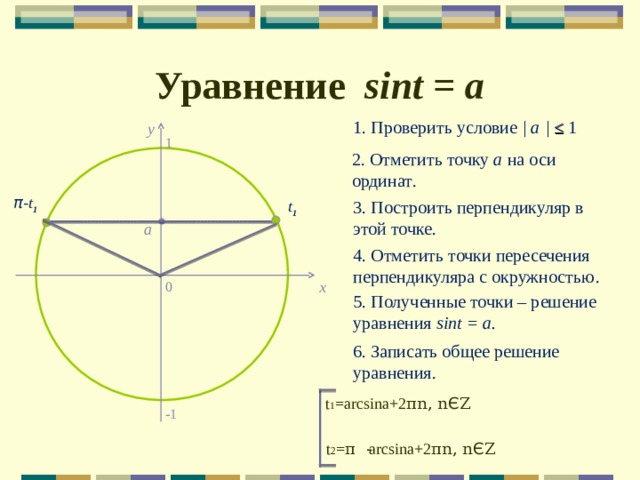
Уравнение sint = a

1 . Проверить условие | a | ≤ 1

y

1

2 . Отметить точку а на оси ординат .

π -t 1

3 . Построить перпендикуляр в этой точке .

t 1

a

4 . Отметить точки пересечения перпендикуляра с окружностью .

x

0

5 . Полученные точки – решение уравнения sint = a.

6 . Записать общее решение уравнения .

t 1 =arcsina+2 π n, n Є Ζ

-1

t 2 = π -

arcsina+2 π n, n Є Ζ

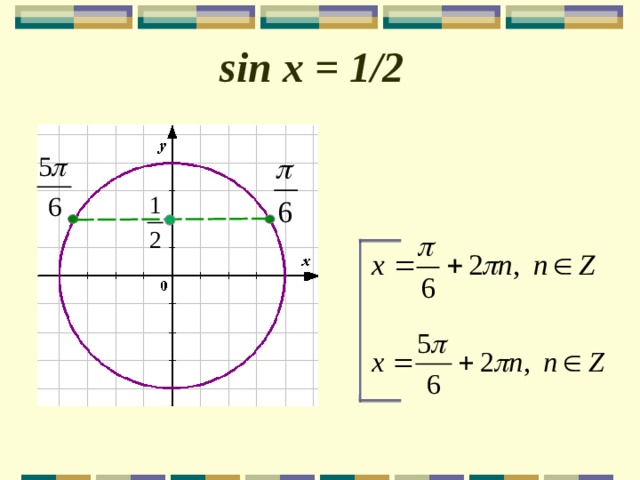
sin x = 1/2

( -

;

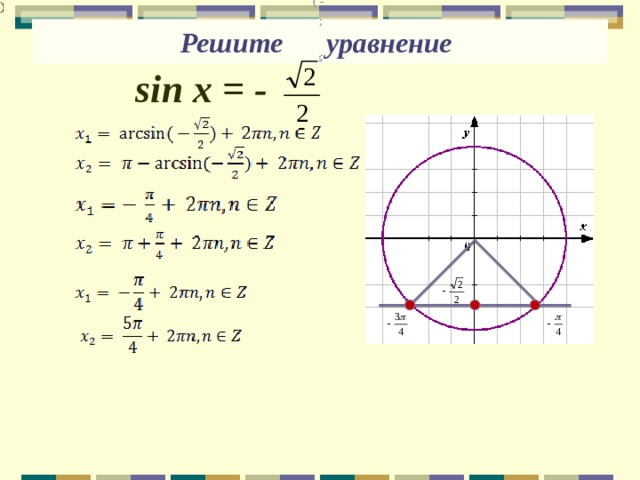
Решите уравнение

,

;

,

sin х = -

2sin x-1 = 0

sin(2x)=½

sin( ) =½

sin( π- )=½

sin(-x) =½

sin(x- π/3 )= ½

sinx cos π/3 +cosx sin π/3=½

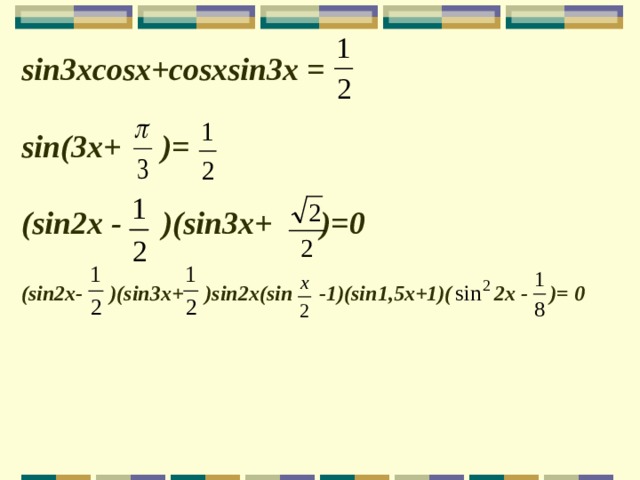
sin3xcosx+cosxsin3x =

sin(3x+ )=

(sin2x - )(sin3x+ )=0

( sin2x- )(sin3x+ )sin2x(sin -1)(sin1,5x+1)( 2x - )= 0

0≤ a ≤1

t=± arcsin + π n,n Z

Спасибо за внимание МОУ гимназия № 11, Харламова Л.Н.

• Презентация «Тригонометрические уравнения», уч. Ткачева М.Н.
• «Решение простейших тригонометрических уравнений», Пуртова Е.Д., г. Оршанка
• Методика изучения тригонометрии в школьном курсе математики. Хазиева Г. И.
• Презентация «Решение тригонометрических уравнений» МОУ СОШ №256, г.Фокино
• http://www.resolventa.ru/spr/trig/equation.htm