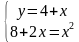Система-следствие

Дата

Тема урока: СИСТЕМА-СЛЕДСТВИЕ

Цели: рассмотреть преобразования уравнений, приводящих к системам-следствиям; закрепить навыки решения систем уравнений в ходе решения примеров.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Продолжаем с вами работать с системами уравнений и методами их решений. Прежде чем мы перейдем к теме сегодняшнего урока, попрошу вас выполнить самостоятельную работу. Она по вариантам (в таблице ниже). Решаем ТОЛЬКО СПОСОБОМ ПОДСТАНОВКИ. Во всех, кроме 3го варианта, в ответе целые числа. Фото самостоятельной работы с полным решением высылаете мне. Не забывайте про область существования функций.

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Откройте тетради и запишите сегодняшнее число и тему урока. Сегодня мы рассмотрим те преобразования, применяемые к уравнениям, которые не приводят к равносильной системе, а к системе-следствию. Это следующие преобразования:

- возведение в четную степень;

- потенцирование;

- избавление от знаменателя.

Чтобы вам было легче понять мои решения, приведенные ниже, перейдите по ссылке и посмотрите видеоурок.

http://1tvcrimea.ru/content/domashnee-zadanie-11-klass-russkiy-yazyk-khimiya-algebra-vypusk-ot-3042020

В этом видео достаточно подробно разбираются задания ИЗ ВАШЕГО УЧЕБНИКА ПО АЛГЕБРЕ. И этот видеоурок будет ОЧЕНЬ ПОЛЕЗЕН ПРИ ВЫПОЛНЕНИИ ДОМАШНЕГО ЗАДАНИЯ. Тот, кто его посмотрит, когда будет решать д/з, поймет что я имела в виду под «полезен».

Пример 1. Решить систему уравнений

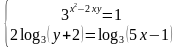
Решение.

Первое уравнение у нас показательное, и правую его часть необходимо привести к основанию 3. Второе уравнение – логарифмическое с одинаковыми основаниями, но в левой части находится коэффициент 2, его необходимо занести в степень числа логарифма.

Не забывайте про ОДЗ:

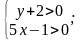
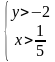
ОДЗ найдено. Возвращаемся к решению системы. Применим преобразования, написанные выше, получим:

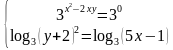
Пропотенцируем уравнение, тогда:

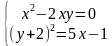
В первом уравнении системы вынесем «х» за скобки, во втором применим формулу сокращенного умножения:

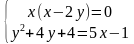
Видим, что первое уравнение системы является распадающимся. Решим его отдельно:

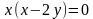
Получим, что

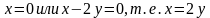
Посмотрим на ОДЗ: х=0 нам не подходит, значит далее будем решать способом подстановки систему следующего вида:

; ;

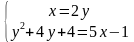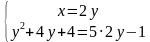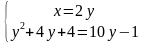
Видим, что второе уравнение зависит только от одной переменной. Решим его:

; ; .

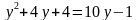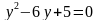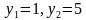Оба значения переменной «у» по ОДЗ подходят. Вернемся к подстановке:

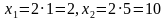
Ответ: (2; 1), (10; 5).

Пример 2. Решить систему уравнений

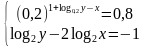
Решение. Выпишем с вами ОДЗ:

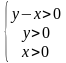
В первом уравнении системы необходимо левую часть расписать с помощью правила работы со степенью с одинаковым основанием. Во втором уравнении необходимо поработать с логарифмами и применить следующие свойства (первое из свойств применяется к первому уравнению):

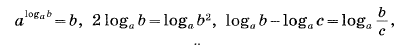
Тогда получим систему:

; ;

;

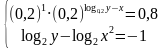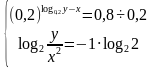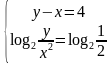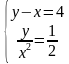
Решим эту систему способом подстановки. Из первого уравнения выразим переменную «у», а во втором умножим каждую часть уравнения на «2х²», чтобы избавится от знаменателей. Получим:

; ;

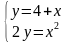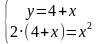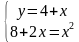
Решим отдельно второе уравнение системы. Получим следующие корни:

Вернемся к подстановке и найдем переменную «у»:

Ответ: (4; 8).

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Открываете учебники на странице 343 и выполняете самостоятельно №14.20(а). Не забывайте про ОДЗ.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: №14.32(а).
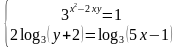
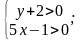
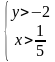
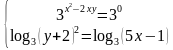
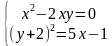
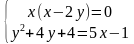
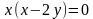
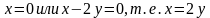
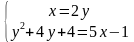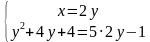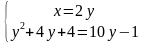
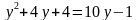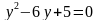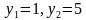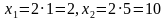
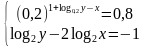
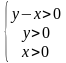
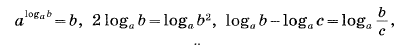
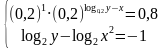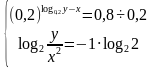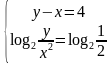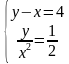
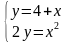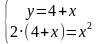