Тема: Кодирование информации. Алгоритмы перевода.
Позиционная система: значение цифры определяется ее позицией в записи числа.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
Система счисления - это совокупность приемов и правил записи чисел с помощью определенного набора символов (некоторый способ кодирования числовой информации).
Разнообразные системы счисления, которые существовали раньше и используются в наше время, можно разделить на непозиционные и позиционные. Знаки которые используются при записи чисел, называются цифрами.
Сначала рассмотрим непозиционные системы счисления.
Рассмотрим непозиционные системы счисления.
Остановимся поближе на Римской непозиционной системой счисления.
Римской системе в качестве цифр используются латинские буквы.
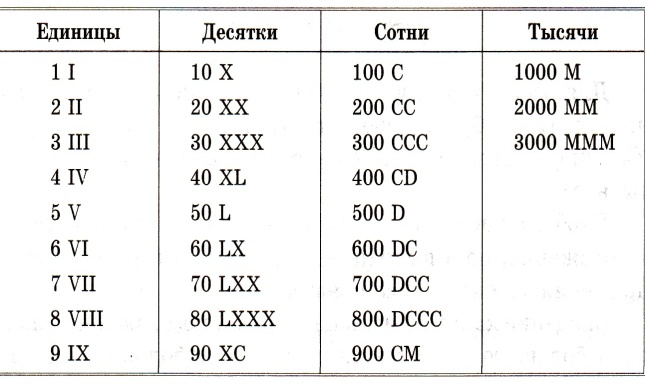
В римских числах цифры записываются слева направо в порядке убывания.
В таком случае их значения складываются.
Если же слева записана меньшая цифра, а справа - большая, то их значения вычитаются.
Пример:
CCXXXII=100+100+10+10+10+1+1=232
VI=5+1=6
IV=5-1=4
MCMXCVIII= =1000+(-100+1000)+(-10+100)+5+1+1+1=1998
Теперь поговорим о позиционных системах счисления.
Создание позиционных систем счисления позволили записывать сколь угодно большие числа с помощью небольшого количества цифр, а также возникла возможность упростить выполнение арифметических операций над числами.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Позиция цифры в числе называется разрядом.
Каждая позиционная система счисления имеет определенный алфавит цифр и основание.
Основание – это количество используемых цифр.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр: 0,1,2,3,4,5,6,7,8,9.
Позиционный характер этой системы легко понять на примере любого многозначного числа. Например в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы.
Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при пп первых арабских цифр, а при п10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем.
| Система счисления | основание | Алфавит |
| Десятичная | п=10 | 0,1,2,3,4,5,6,7,8,9 |
| Двоичная | п=2 | 0,1 |
| Восьмеричная | п=8 | 0,1,2,3,4,5,6,7 |
| Шестнадцатеричная | п=16 | 0,1,2,3,4,5,6,7,8,9, А(10), В(11), C(12), D(13),E(14),F(15) |
Если требуется указать основание системы счисления, к которой относится число, то оно приписывается нижним индексом к этому числу.
Например: 1011012, 765810, 3В8А16
В системе счисления с основанием q единицами разрядов служат последовательные степени числа q. q единиц какого либо разряда образуют единицу следующего разряда. Для записи числа в q-ричной системе счисления требуется q различных цифр, изображающих числа 0,1,…, q-1.
Развернутой формулой числа называется запись в виде:
Аq=an*qn+an-1*qn-1+…+a0*q0+a-1*q-1+ …+a-m*q-m
где
Аq = само число
q-основание системы счисления
а – цифры данной системы счисления
п – число разрядов
Развернутая форма числа в двоичной системе счисления:
А2=an*2n+an-1*2n-1+…+a0*20+a-1*2-1+ …+a-m*2-m
Пример: Получить развернутую форму десятичных чисел:
3247810=3*104+2*103+4*102+7*101+8*100





Сравнение чисел в различных системах счисления
Пример. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
2316, 328, 111102.
Решение. Переведём все числа в десятичную систему счисления:
2316 = 3510;
328 = 2610;
111102 = 3010. Таким образом, наибольшим среди этих трёх чисел является число 35.
Ответ: 35.
Задачи для тренировки:
1. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
3816, 758, 1101002.
2. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
1416, 268, 110002.
3. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
2416, 508, 1011002.
4. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
5016, 1068, 10010102.
5. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
5016, 1068, 10010102.
Как представлено число 8310 в двоичной системе счисления?
1) 10010112 2) 11001012 3) 10100112 4) 1010012
Сколько единиц в двоичной записи числа 195?
Сколько единиц в двоичной записи числа 173?
Как представлено число 25 в двоичной системе счисления?
1) 10012 2) 110012 3) 100112 4) 110102
Как представлено число 82 в двоичной системе счисления?
1) 10100102 2) 10100112 3) 1001012 4) 10001002
Как представлено число 263 в восьмеричной системе счисления?
1) 3018 2) 6508 3) 4078 4) 7778
Как записывается число 5678 в двоичной системе счисления?
1) 10111012 2) 1001101112 3) 1011101112 4) 111101112
Как записывается число A8716 в восьмеричной системе счисления?
1) 4358 2) 15778 3) 52078 4) 64008
Как записывается число 7548 в шестнадцатеричной системе счисления?
1) 73816 2) 1A416 3) 1EC16 4) A5616
Ответы
| 61 |
| 24 |
| 44 |
| 80 |
| 70 |
| 3 |
| 4 |
| 5 |
| 2 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |























