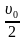Тема: Скорость прямолинейного равноускоренного движения. График скорости
Цели урока: Расширить взгляды учащихся на природу механического движения. Научиться строить график скорости от времени. Развитие навыков самостоятельной работы.
Ход урока
Повторение. Проверка домашнего задания
-
Дайте определение мгновенной скорости.
-
Каков физический смысл мгновенной скорости?
-
Что такое ускорение?
-
Назовите единицы ускорения.
-
Как рассчитывается мгновенная скорость при равноускоренном движении?
-
Чем отличаются векторные величины от скалярных?
-
Что показывает модуль вектора ускорения?
-
Каковы правила сложения векторных величин?
-
Какое движение называют равноускоренным?
-
По какой формуле находится ускорение?
-
Что характеризует ускорение?
С целью повторения материала можно предложить учащимся ряд простых устных задач по изученной теме:
-
Какой путь пройдет велосипедист за 2 ч, если его средняя скорость 15 км/ч?
-
Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории?
-
О какой скорости - средней или мгновенной - идет речь в следующих случаях:
а) пуля вылетает из винтовки со скоростью 800 м/с;
б) самолет летит из Киева в Москву со скоростью 800 км/ч;
в) скоростемер на тепловозе показывает 75 км/ч?
Работа по карточкам
Карточка № 1
-
При равноускоренном движении скорость тела за 5 с увеличилась на 4 м/с. Найдите ускорение тела.
-
Если при равноускоренном движении скорость тела за 2 с изменилась на 4 м/с, то за последующие 3 с она изменится на .
Карточка № 2
-
Если при равноускоренном движении скорость тела за 3 с изменилась на 6 м/с, то изменение скорости на 4 м/с произойдет за .
-
За 5 с до финиша скорость велосипедиста равнялась 18 км/ч, а на финише 25,2 км/ч. Определите ускорение, с которым финишировал велосипедист.
Карточка № 3
-
При подходе к станции поезд уменьшил скорость от 90 км/ч в течение 25 с. Определите ускорение поезда.
-
Если при равноускоренном движении скорость тела за 4 с изменилась на 8 м/с, то за следующую секунду она изменится на .
Изучение нового материала
План изложения нового материала:
-
Вычисление скорости при равноускоренном движении.
-
Построение графиков зависимости скорости от времени.
-
Средняя скорость движения.
Скорость при равноускоренном движении
Теория равноускоренного движения была разработана Галилео Галилеем. Галилей впервые дал определение равноускоренного движения, доказал ряд теорем, которые описывали закономерности этого движения.
Изучение равноускоренного движения опирается на основное соотношение, которое определяет ускорение тела: 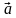 =
=  , из этой формулы выразим скорость прямолинейного равноускоренного движения:
, из этой формулы выразим скорость прямолинейного равноускоренного движения: 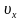 =
= 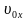 +
+ 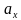 ·t.
·t.
Если тело начинает равноускоренное движение из состояния покоя, т. е. 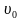 = 0, то скорость тела в любой момент времени определяется так:
= 0, то скорость тела в любой момент времени определяется так: 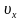 =
= 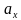 ·t.
·t.
Построение графиков зависимости скорости от времени
Наглядно движение тела можно представлять в виде графиков.
Зависимость скорости тела от времени называют законом изменения скорости, а графическое представление этого закона - графиком скорости. Чтобы построить график скорости, оси прямоугольной системы координат обозначаются так: по оси х откладывают время, а по оси у - значения скорости тела.
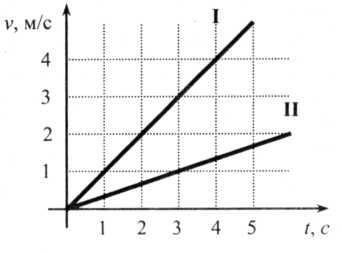
- На рис. 1 представлены два графика равноускоренного движения из состояния покоя. Ускорение первого тела равно 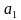 = 1 м/с2, а второго -
= 1 м/с2, а второго - 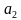 = 3 м/с2.
= 3 м/с2.
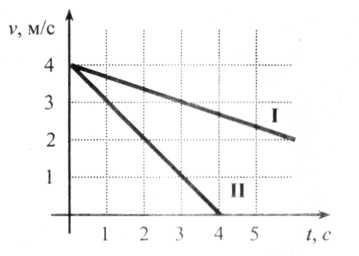
- На рис. 2 показаны графики равнозамедленного движения: ускорение первого тела равно 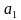 = -
= - 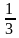 м/с2, а второго -
м/с2, а второго -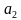 =-1 м/с2.
=-1 м/с2.
- При помощи графика скорости мы всегда можем найти скорость тела в любой момент времени. По виду графика скорости можно судить о характере движения тела.
Средняя скорость движения
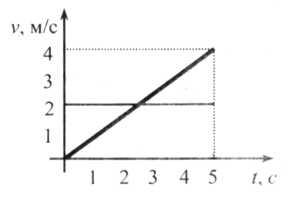
Из графика скорости вытекает, что при 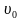 = 0 в равноускоренном движении средняя скорость на отрезке времени t всегда равна половине достигнутой скорости
= 0 в равноускоренном движении средняя скорость на отрезке времени t всегда равна половине достигнутой скорости 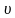 (рис. 3), т. е.:
(рис. 3), т. е.: 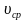 =
= 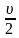
- При равнозамедленном движении средняя скорость определяется так: 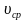 =
= 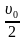
- При условии, что конечная скорость тела 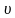 = 0.
= 0.
Закрепление изученного материала
- Учитель строит возможные варианты графиков и комментирует их (рис.).
По графику зависимости скорости от времени можно найти ускорение: 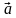 =
= 
Задание 1
Записать уравнение скорости от времени 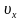 (t) для каждого участка графика на рисунке.
(t) для каждого участка графика на рисунке.
Решение:
-
Участок ОА: 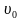 = 0, а =
= 0, а =  = 20 м/
= 20 м/ . Уравнение
. Уравнение 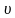 = 20t;
= 20t;
-
Участок АВ: 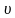 =
= 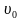 = 60, а = 0. Уравнение
= 60, а = 0. Уравнение 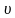 = 60;
= 60;
-
Участок BD: 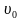 = 60 м/с,
= 60 м/с, 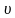 = - 60 м/с, а =
= - 60 м/с, а =  = - 60 м/
= - 60 м/ .
.
Уравнение 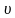 = 60 - 60t;
= 60 - 60t;
-
Участок DF: 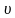 =
= 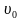 = - 60, а = 0. Уравнение
= - 60, а = 0. Уравнение 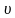 = - 60.
= - 60.
Задание 2
На рис. показаны тела, их скорости и ускорения. Запишите уравнения скорости для каждого тела и определите скорость через 5 с после начала движения.
-
 = 2t; через 5 с:
= 2t; через 5 с: 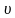 = 10 м/с;
= 10 м/с;
-
 = 8 + 2t через 5 с:
= 8 + 2t через 5 с: 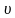 = 8 м/с + 5 с · 2 = 18 м/с;
= 8 м/с + 5 с · 2 = 18 м/с;
-
 = 8t; через 5 с:
= 8t; через 5 с: 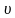 = 8 м/с - 5 с · 2 = 2 м/с;
= 8 м/с - 5 с · 2 = 2 м/с;
-
 = - 8 - 2t; через 5 с:
= - 8 - 2t; через 5 с: 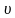 = - 8 м/с - 2 · 5 с = - 18 м/с; Модуль скорости
= - 8 м/с - 2 · 5 с = - 18 м/с; Модуль скорости  = |
= |  | = 18 м/с;
| = 18 м/с;
-
 = 1; через 2 с:
= 1; через 2 с: 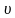 = 1 м/с.
= 1 м/с.
- Постройте график зависимости 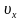 от t для пятого тела. Что будет графиком функции?
от t для пятого тела. Что будет графиком функции?
(Прямая, параллельная оси t.)
- А что будет графиком зависимости для остальных четырех тел? (Прямая.)
В данном случае имеем линейную зависимость.
З адание 3
-
По графику скорости I определить ускорение тела и скорость тела через 6 с, 10 с.
-
По графику скорости II определить ускорение и скорость тела через 4 с.
-
По графику скорости III определить ускорение и скорость тела через 16 с.
Задание 4 (Работа с таблицей)
| Вид графиков зависимости проекции вектора скорости от времени при равноускоренном движении |
|
| Векторы   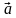 . . | Векторы   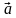 |
|
Вид графиков |
| |
|
По графикам 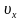 (t) можно определить: (t) можно определить: |
| Начальную скорость 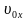 | 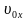 = 1 м/с = 1 м/с
| 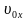 = 4 м/с = 4 м/с
|
| Скорость в любой момент времени | 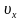 (2с) = 3 м/с (2с) = 3 м/с
| 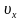 (2с) = 2,5 м/с (2с) = 2,5 м/с
|
| Найти ускорение, с которым движется тело 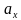 = =  | 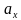 = = = 1 м/ = 1 м/
| 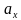 = = = - 0,75 м/ = - 0,75 м/
|
| Составить уравнение зависимости 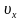 (t): (t): 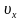 = = 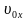 + + 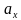 ·t ·t | 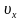 = 1 + 1t = 1 + t = 1 + 1t = 1 + t
| 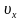 = 4 - 0,75t = 4 - 0,75t
|
Решение задач
Задача 1
В одитель нажимает на тормоз в тот момент, когда спидометр показывает 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 2 м/с2?
Домашнее задание: §6; упр. 6. Сборник № 150






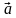 =
=  , из этой формулы выразим скорость прямолинейного равноускоренного движения:
, из этой формулы выразим скорость прямолинейного равноускоренного движения: 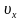 =
= 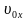 +
+ 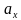 ·t.
·t.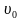 = 0, то скорость тела в любой момент времени определяется так:
= 0, то скорость тела в любой момент времени определяется так: 
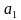 = 1 м/с2, а второго -
= 1 м/с2, а второго - 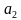 = 3 м/с2.
= 3 м/с2.
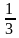 м/с2, а второго -
м/с2, а второго -
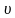 (рис. 3), т. е.:
(рис. 3), т. е.: 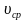 =
=