Скрещивающиеся прямые. Углы с сонаправленными сторонами.

Урок № 12 по геометрии в 10 классе 08.10.20г

Учитель Евтушенко М.С.

Общая тема: Параллельность прямых и плоскостей

Тема: Скрещивающиеся прямые. Углы с сонаправленными сторонами.

Тип урока: урок изучения и первичного закрепления новых знаний.

Планируемые результаты:

Личностные:

Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

Метапредметные:

Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных проблем;

Предметные: умение формулировать определение «скрещивающиеся прямые», объяснять какие два луча называются сонаправленными.

Формы работы: фронтальная, индивидуальная

Образовательные ресурсы: карточки, презентация

ХОД УРОКА

Организационный момент. Анализ самостоятельной работы.

Актуализация опорных знаний.

2.1. Вспомним, как располагаются прямые в пространстве?

Расположение прямых в пространстве:

1. Пересекаются

2. Параллельны

Как располагаются прямые и плоскости в пространстве?

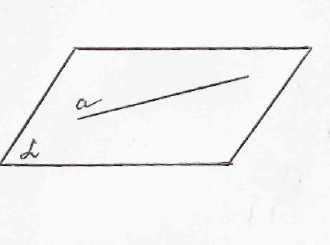
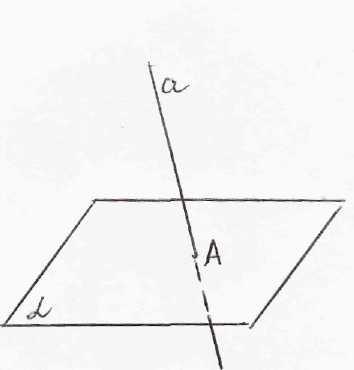
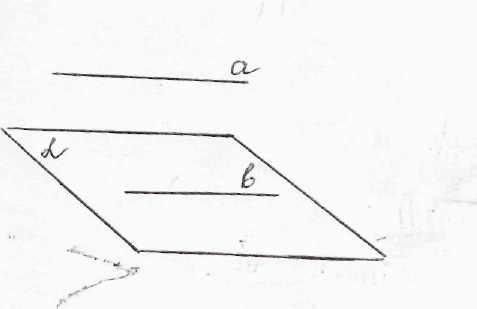
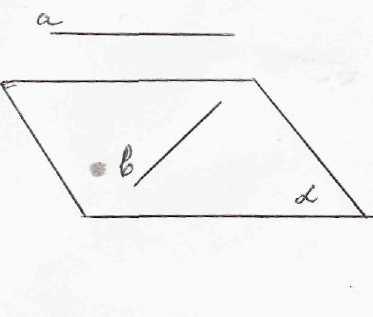
2.2. Мотивация.

Заметим, что последний вид расположения прямых задает их расположение каким-то новым способом.

Это скрещивающиеся прямые.

Определение скрещивающихс прямых:

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

3.1. Постановка целей учащимися

Первичное закрепление знаний.

Рассмотреть различные пары скрещивающихся прямых на моделях многоугольников

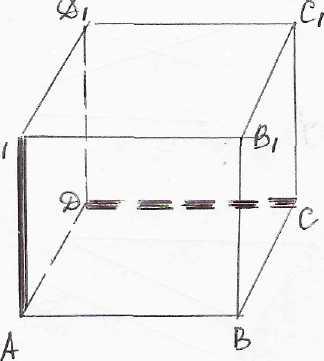
АВСDА₁В₁С₁D₁-куб. АА₁ и DС-скрещивающиеся ребра. В каких плоскостях лежит прямая DС? Как располагается прямая АА₁ по отношению к этим плоскостям?

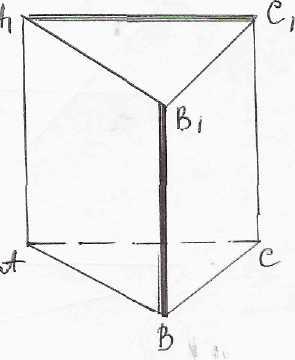
АВСА₁В₁С₁-призма. ВВ₁ и А₁С₁-скрещивающиеся ребра. В каких плоскостях лежит прямая ВВ₁? Как располагается прямая А₁С₁ по отношению к этим плоскостям?

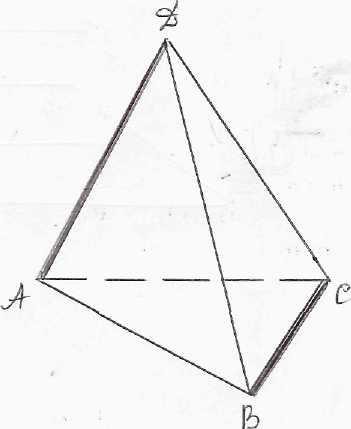
АВСD- пирамида. Рассуждаем аналогично.

Наблюдаем: прямые являются скрещивающимися, если одна прямая лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой.

3.2.Докажем признак скрещивающихся прямых.

Но перед этим поставим проблему

Проблема

• Построить плоскость α, проходящую через точку К и параллельную скрещивающимся прямым а и b.

Построение:

1. Через точку К провести

прямую а₁ || а.

2.Через точку К провести

прямую b₁ || b.

3. Через пересекающиеся

прямые проведем

плоскость α. α – искомая

плоскость.

А теперь проведите самостоятельно доказательство задачи:

• Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Учащиеся самостоятельно доказывают теорему о плоскости, параллельной другой скрещивающейся прямой.

1. Закрепление теоретических знаний.

4.1.Ответить на вопросы:

1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?

2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться; б) быть скрещивающимися?

3. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с ? Ответ обоснуйте.

4. Прямая а скрещивается с прямой в, а прямая в скрещивается с прямой с . Следует ли из этого, что прямые а и с скрещивающиеся?

5. Каково должно быть взаимное расположение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?

6. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся прямых?

7. Даны две пересекающиеся плоскости. В одной из них лежит прямая а, в другой плоскости - прямая в. Лежат ли прямые а и в в одной плоскости, если известно, что они пересекают линию пересечения плоскостей : а) в одной точке; б) в разных точках.

8. Даны две параллельные плоскости . В одной плоскости лежит прямая а, в другой плоскости - прямая в. Каковы взаимные случаи расположения прямых а и в?

9. В плоскости двух параллельных прямых а и в дана точка С, не лежащая на этих прямых. Прямая с проходит через точку С. Как может быть расположена прямая с относительно прямых а и в?

5.Перейдем к практической части урока.

D

Дан куб АВСDA₁B₁C₁D₁ АА₁ || DD₁, как противоположные стороны квадрата, лежат в одной плоскости и не пересекаются.

АА₁ || DD₁; DD₁ || CC₁ →AA₁ || CC₁ по теореме о трех параллельных прямых.

Являются ли АА₁ и DC параллельными? Они пересекаются?

Задача №34.

Дано: D (АВС), АМ = МD; ВN = ND; CP = PК ВN.

Определить взаимное расположение прямых:

а) ND и AB б) РК и ВС в) МN и AB

Решить №36, 39

Задача №42

Дано; ABCD - параллелограмм, АВЕК- трапеция, ЕК || (АВС).

а) Выясните взаимное расположение прямых CD и ЕК.

б) Найдите периметр АВЕК, если АВ = 22,5 см, ЕК = 27,5 см, в трапецию можно вписать окружность.

Домашнее задание: пп. 7,8 выучить определения, теоремы; решить № 35, 38

Рефлексия.

Подведение итогов урока.