Россия, Асбест
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 03.05.2024 07:08
Якубова Альбина Рифкатовна
Учитель математики
50 лет
1 211
41 602 
Местоположение
Специализация
" Сложение вероятностей"
Категория:
Математика
18.05.2022 19:39
Просмотр содержимого документа
«" Сложение вероятностей"»
Сложение вероятностей
Повторение
Что называется суммой (объединением) событий А и В?
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
Пример: в ящике находится красный, черный и белый шары.
А- извлечение черного шара
В- извлечение красного шара
С- извлечение белого шара
А+В – извлечен черный или красный шар
В+С – извлечен красный или белый шар
А+С – извлечен черный или белый шар
Повторение
Что называется произведением (пересечением) событий А и В?
Произведением событий А и В называют событие, которое наступает тогда и только тогда, когда наступает и событие А и событие В.
Оно обозначается А·В или АВ.
Пример1.
Дать описание произведения АВ событий А и В, если
а) А-цена товара больше 100 руб.;
В -цена товара не больше 110руб.;
100 ≤110
б)А-завтра пятница, В-завтра 13–е число;
Завтра пятница 13-ое
в)А- координаты случайно выбранной точки на плоскости удовлетворяют неравенству x²+y²≤1;
В- координаты случайно выбранной точки положительны;
·
(x;y)
г) А- случайно выбранное двузначное число четно;
В- случайно выбранное число делится на 11.
{22, 44, 66, 88}
Теорема сложения вероятностей
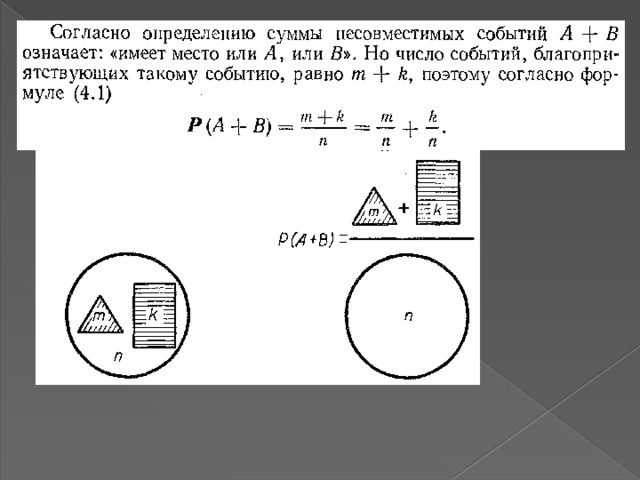
Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Вероятность появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий:
Сумма вероятностей попарно несовместных событий, образующих полную группу равна 1 .
Теорема сложения вероятностей
Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Пример
Пример
Сумма вероятностей противоположных событий равна 1
Теорема сложения вероятностей
назад
m
ɩ
Теорема сложения вероятностей
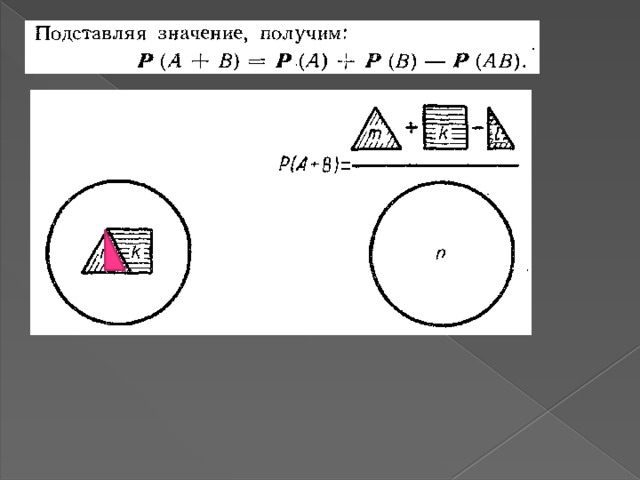
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления(произведения):
назад
Пример
Пример
Вероятность произведения независимых событий
Пример:
© 2022, Якубова Альбина Рифкатовна 1299 112
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
