Воронцова Ольга Владимировна,
учитель математики, МБОУ СОШ №80 г. Новосибирска,
630098 г. Новосибирск, ул. Энгельса, 6, e-mail: vov1975_3@mail.ru
Роженко Тамара Ивановна,
учитель информатики, МБОУ СОШ №80 г. Новосибирска,
630098 г. Новосибирск, ул. Энгельса, 6, e-mail: tiroz@ngs.ru
Сложности в решении задач на проценты, сплавы и смеси при подготовке к ОГЭ в рамках интегрированного курса по математике и информатике
Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому любой экзамен по математике (ОГЭ или ЕГЭ), любая проверка знаний содержат в качестве основной и, пожалуй, наиболее трудной части решения задач.
Научить решать большинство текстовых задач, содержащихся в открытом банке, можно практически любого выпускника. Конечно, при этом определяющими факторами являются желание и стремление ученика, и владение вычислительными навыками. Мы хотим показать прием решения задач на растворы, смеси и сплавы, не только с помощью математики, но и информатики. Исходя из опыта учителя математики, именно такой тип задач вызывают основные трудности, поэтому их для лучшего усвоения надо рассматривать как на уроках математики, так и на информатике.
В качестве практического материала нами были использованы задачи «от составителей» из «открытого банка заданий».
Существует много способов решения задач на растворы, смеси и сплавы. Мы хотим остановится на одном из них, который, по нашему мнению, самый простой для усвоения решения таких задач – табличный.
Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
1) Что такое концентрация вещества в растворе, смеси, сплаве? Концентрация вещества в растворе (смеси, сплаве) – это отношение массы или объема вещества к массе или объему всего раствора (смеси, сплава). Как правило, концентрация выражается в процентах.
2) Что такое процент? Процент – это сотая доля числа. Она может выражаться либо в виде десятичной дроби, либо в виде процента.
3) Что такое масса раствора, смеси, сплава? Масса раствора (смеси, сплава) равна сумме масс всех составляющих. При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов. Масса растворенного вещества при смешивании двух растворов суммируется.
Задачи на смеси и сплавы бывают двух основных видов:
-
Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
-
В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Алгоритм решения задачи на сплавы, растворы и смеси:
-
изучить условия задачи;
-
выбрать неизвестную величину (обозначить ее буквой);
-
определить все взаимосвязи между данными величинами;
-
составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;
-
провести анализ результата.
Рассмотрим несколько задач и решим их с помощью таблицы.
Задача 1. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
В этой задаче примем за x массу первого сплава и выразим через него второй и третий.
|
| Масса сплава | Процентное содержание вещества | Масса вещества |
| Первый сплав | x | 10%=0,1 | 0,1 x |
| Второй сплав | x +3 | 40%=0,4 | 0,4 (x+3) |
| Третий сплав (результат слияния первых двух) | 2x+3 | 30%=0,3 | 0,3 (2x+3) |
Составим и решим уравнение:
0,1x+0,4 (x+3)= 0,3 (2x+3)
0,1х+ 0,4х+1,2=0,6х+0,9
0,3=0,1х
х=3 (кг) масса первого сплава.
2*3+3=9 (кг) масса третьего сплава.
Ответ: масса третьего сплава 9 кг.
Задача 2. Смешав 60%-й и 30%-й растворы кислоты и добавив 5 кг чистой воды, получили 20%-й раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%-го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Для решения этой задачи будем составлять две краткие записи. До слов "если бы вместо 5кг воды..." и после. Примем за х массу первого раствора, а за y – массу второго.
|
| Масса раствора | Процентное содержание вещества | Масса вещества |
| Первый раствор | x | 60%=0,6 | 0,6 x |
| Второй раствор | y | 30%=0,3 | 0,3y |
| Вода | 5 | 0 | 0 |
| Третий раствор (результат слияния первых двух) | x+y+5 | 20%=0,2 | 0,2 (x+y+5) |
Составим уравнение с двумя переменными: 0,6 x + 0,3y+ 0= 0,2 (x+y+5)
|
| Масса раствора | Процентное содержание вещества | Масса вещества |
| Первый раствор | x | 60%=0,6 | 0,6 x |
| Второй раствор | y | 30%=0,3 | 0,3y |
| Раствор | 5 | 90%=0,9 | 4,5 |
| Третий раствор (результат слияния первых двух) | x+y+5 | 70%=0,7 | 0,7 (x+y+5) |
Составим уравнение с двумя переменными: 0,6 x + 0,3y+ 4,5= 0,7 (x+y+5)
Объединив полученные два уравнения в систему и решив ее, получим x. Это и будет сколько килограммов 60%-го раствора использовали для получения смеси. Ответ: 2 кг.
Для нас важным является практический аспект в решении математических задач, поскольку в настоящее время выпускник, даже хорошо знающий математику, но не умеющий применять математические методы на компьютере, не может считаться успешным. Поэтому необходимо научить детей проводить требуемые вычисления на компьютере.
Наиболее универсальным для решения рассматриваемого класса задач является табличный процессор Excel.
Для решения задачи 1 в электронных таблицах изменим форму расчетов. В начало таблицы поместим известные данные, во второй столбец расчеты, в третий – расчет результата:
|
| A | B | C | D |
| 1 | | Процентное содержание вещества |
| Масса сплава |
| 2 | Первый сплав | 0,1 | | =C5/C6 |
| 3 | Второй сплав | 0,4 | =B3*3 | =D2+3 |
| 4 | Третий сплав | 0,3 | =B4*3 | =D2+D3 |
| 5 | | | =C3-C4 | |
| 6 | | | =B4*2-B3-B2 | |
Получаем:
|
| A | B | C | D |
|
| | Процентное содержание вещества | | Масса сплава |
| 1 | Первый сплав | 0,1 | | 3 |
| 2 | Второй сплав | 0,4 | 0,9 | |
| 3 | Третий сплав | 0,3 | 1,2 | |
| 4 | | | 0,3 | |
| 5 | | | 0,1 | |
Задачу 2 решаем в Excel матричным методом. используем полученную систему линейных уравнений. Составляем матрицу, помещаем ее в Excel:
|
| A | B | C | D |
| 1 | 0,4 | 0,1 |
| 1 |
| 2 | 0,1 | 0,4 |
| 1 |
Для нахождения обратной матрицы используем функцию МОБР:
| 2,666666667 | -0,666666667 |
| -0,666666667 | 2,666666667 |
Для умножения обратной матрицы на массив свободных членов используем функцию МУМНОЖ. Получаем массив из двух двоек, которые являются корнями системы уравнений.
Умение решать системы уравнений в Excel – очень полезный навык для учащихся. Они учатся проверять математическое решение на компьютере, искать подходящие методы, что расширяет кругозор и учит решать задачи различными способами.
Таким образом, учащиеся закрепляют знания, полученные на уроках математики и осваивают способы решения задач на компьютере.
Заключение
В задачах этого типа прослеживается системный подход к решению задач. Происходит успешная отработка и закрепление интеллектуальных умений (анализ, синтез, аналогия, обобщение. конкретизация и т.д.). Данная система задач на смеси, растворы и сплавы была апробирована в ходе КПР (контрольно-проверочной работы) по математике в 8 классе в 2016-17 учебном году. Опыт показал, что учащиеся не знавшие вначале, как подойти к решению этих задач, в конце темы успешно заполняли таблицу и получали верный ответ.
Литература:
1. Открытый банк заданий ОГЭ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge;
2. https://oge.sdamgia.ru Каталог заданий. Задачи на проценты, сплавы и смеси
3. В.Я. Гельман. Решение математических задач средствами Excel: Практикум. – СПБ.: Питер, 2003.
Дополнение:
В математике есть ряд текстовых задач, которые вызывают затруднение у учащихся при их решении. К таким задачам можно отнести задачи на растворы, смеси и сплавы. Практическое значение этих задач огромно. Встречаются они при изучении смежных дисциплин, например, химии. Самостоятельно справиться с ними могут немногие. Вместе с этим они являются хорошим средством развития мышления учащихся.
Трудности при решении этих задач могут возникать на различных этапах:
-
составления математической модели (уравнения, системы уравнений, неравенства и т. п.;
-
решения полученной модели;
-
анализа математической модели (по причине кажущейся ее неполноты: не хватает уравнения в системе и пр.).
Все сложности преодолимы при тщательном анализе задачи. Основными компонентами в этих задачах являются:
При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.
Этапы решения задачи:
1. Знакомство учащихся с текстом задач и выделение основных компонентов в них. Заполнение таблицы.
Таблица для решения задач имеет следующий вид:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| |
| | |
2. Составление уравнения и его решение.
3. Анализ полученных данных, ответ на вопрос задачи.
Рассмотрим решение задач с применением таблицы.
Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.
Решение:
| Наименование веществ, смесей | Масса раствора (смеси, сплава) М, кг | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m, кг |
| Исходный раствор | 2 | 80 % = 0,8 | 0,8·2 |
| Вода | 3 | - | - |
| Новый раствор | 5 | х % = 0,01х | 0,01х·5 |
Масса уксусной кислоты не изменилась, тогда получаем уравнение:
0,01х·5 = 0,8·2; 0,05х = 1,6; х = 1,6:0,05; х = 32.
Ответ: 32 %.
Задача 2. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение:
| Наименование веществ, смесей | Масса раствора (смеси, сплава) М, г | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m, г |
|
| Исходный раствор | 200 | 70 % | 0,7·200 |
|
| Вода | х | - | - |
|
| Новый раствор | 200 + х | 8 % | 0,08(200 + х) |
|
Анализируя таблицу, составляем уравнение :
0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550.
Ответ :1,55 кг воды.
Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.
Решение:
| Наименование веществ, смесей | Масса раствора (смеси, сплава) М, г | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m, г |
| I раствор | х | 12 % | 0,12х |
| II раствор | х | 20 % | 0,2х |
| Смесь | 2х | 0,32х/2х * 100% | 0,12х+ 0,2 х = 0,32х |
Анализируя таблицу, получаем :
0,32х/2х * 100% = 16 %
Ответ : 16 %.
Задача 4. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| Первый сплав | х | 60% | 0,6 х |
| Второй сплав | у | 45% | 0,45 у |
| Новый сплав | х + у | 55% | 0,6 х + 0,45у |
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение: 0,55(x + y) = 0,6 х + 0,45у;
0,55 х + 0,55 у = 0,6 х+ 0,45 у; 0,05 х = 0,1 у . Выразим x через y: х = 2 у.
Следовательно, отношение, в котором нужно взять сплавы 1:2.
Ответ: 1:2
Задача 5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| Первый сплав | х | 5% | 0, 05 х |
| Второй сплав | х + 4 | 13% | 0,13(х +4) |
| Новый сплав | 2х + 4 | 10% | 0, 05 х + 0,13(х +4)=0,18 х + 0,52 |
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение: 0,1(2x + 4) = 0,18 х + 0,52; 0,02 х = 0,12; х = 6.
Откуда масса третьего сплава равна 16 кг.
Ответ:16 кг.
Задача 6. Смешали некоторое количество 10 % раствора некоторого вещества с таким же количеством 12 % раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| 1 | х | 10% | 0, 1 х |
| 2 | х | 12% | 0,12 х |
| 3 | 2х | (0, 22 х / 2х)* 100 % | 0, 1 х + 0,12х = 0,22 х |
Пусть взяли х г 10-процентного раствора, тогда взяли и х г 12-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. Концентрация получившегося раствора равна 0, 22 х / 2х или 11%.
Ответ: 11%.
Задача 7. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М, кг | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества M, кг |
| Первый раствор | 4 | х % | 0,04 х |
| Второй раствор | 16 | у % | 0,16 у |
| Смесь 1 | 20 | 57% | 0,04 х + 0,16у |
| Смесь 2 | 4+4 =8 | 60 % | 0,04х + 0,04 у |
Пусть концентрация первого раствора – х %, концентрация второго раствора – y %. Составим систему уравнений согласно условию задачи:


0,57 * 20 = 0,04 х + 0,16у, х = 65,
0,6 * 8 = 0,04х + 0,04 у; у = 55.
Таким образом, в первом растворе содержится 0,65 * 4 = 2,6 килограмма кислоты
Ответ: 2,6
Задача 8. Смешав 60% и 30% растворы кислоты и, добавив 5 кг чистой воды, получили 20% раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90% раствора той же кислоты, то получили бы 70% раствор кислоты. Сколько килограммов 60% раствора использовали для получения смеси?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М, кг | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества M, кг |
| Первый раствор | х | 60 % | 0,6 х |
| Второй раствор | у | 30 % | 03 у |
| Смесь 1 | х + у +5 | 20 % | 0,6 х + 0,3у |
| Третий раствор | 5 | 90 % | 0,9* 5 = 4,5 |
| Смесь 2 | х + у +5 | 70 % | 0,6х + 0,3 у + 4,5 |
Пусть х кг и у кг — массы первого и второго растворов, взятые при смешивании. Тогда (х + у +5) кг — масса полученного раствора, содержащего (0,6 х + 0,3у) кг кислоты. Концентрация кислоты в полученном растворе 20 %, значит 0,2(х + у +5) %. Концентрация кислоты во втором растворе 70 %, значит 0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5. Решим систему двух полученных уравнений:
0 ,2(х + у +5) = 0,6 х + 0,3у,
,2(х + у +5) = 0,6 х + 0,3у,
0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5;


 0,4 х + 0,1 у = 1, х =2,
0,4 х + 0,1 у = 1, х =2,
0,1 х + 0,4 у = 1; у = 2.

Ответ: 2 кг.
Задача 9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| Первый сплав | х | 10% | 0, 1 х |
| Второй сплав | 200-х | 30% | 0,3(200-х) |
| Новый сплав | 200 | 25% | 0, 1 х + 0,3(200-х )= 0,25*200 |
Решим уравнение: 0, 1 х + 0,3(200-х )= 0,25*200; х = 50.
Масса второго сплава 150 кг.
Ответ: на 100 кг.
Задача 10. Имеется два куска слитка олова и свинца, содержащие 40% и 60% олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 граммов сплава, содержащего 45% олова?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества m |
| Первый кусок | х | 40% | 0, 4 х |
| Второй кусок | 600-х | 60% | 0,6 (600-х) |
| Новый сплав | 600 | 45% | 0, 4 х + 0,6(600-х )= 0,45*600 |
Решим уравнение: 0, 4 х + 0,6(600-х )= 0,45*600; х = 450.
Ответ:450 кг и 150 кг.
Задача 11. Кусок сплава меди и цинка массой 36 кг, содержит 45% меди. Сколько килограммов меди нужно добавить к этому куску, чтобы получить новый сплав, содержащий 60% меди?
Решение:
| Наименование веществ, растворов, смесей, сплавов | Масса раствора (смеси, сплава) М, кг | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества M, кг |
| Первый кусок | 36 | 45% | 0, 45 *36 = 16,2 |
| Медь | х | 100% | х |
| Новый сплав | 36 + х | 60 % | 16,2 +х=0,6(36 + х) |
Получаем уравнение: 0, 45 х +х=0,6(36 + х), х = 13,5
Ответ: 13,5 кг
Задача 12. Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного в третьем сосуде сиропа и концентрацию сахара в нем.
Решение:
| Наименование веществ, смесей | Масса раствора (смеси, сплава) М, кг | % содержание вещества (доля содержания вещества) m / M * 100% | Масса вещества M, кг |
|
| I сосуд | 4 | 70 % | 0,7·4=2,8 |
|
| II сосуд | 6 | 40 % | 0,4·6 = 2,4 |
|
| III сосуд | х | у % | 0,01ху |
|
| I и III сосуды | 4+х | 55 % | 0,55(4+х) = 2,8+0,01ху |
|
| II и III сосуды | 6+х | 35 % | 0,35(6+х) = 2,4+0,01ху |
|
Итак, получаем систему уравнений :
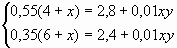

Ответ :1,5 кг сахарного сиропа 15 % концентрации.
Задачи для самостоятельного решения:
13. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 8,7
14. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Ответ: 19,5
15. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 2.
16. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 15,6
17. Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Ответ: 18,6
18. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 11
19. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
20. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
21. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Ответ: 58.
Заключение
В задачах этого типа прослеживается системный подход к решению задач. Происходит успешная отработка и закрепление интеллектуальных умений (анализ, синтез, аналогия, обобщение. конкретизация и т.д.). Данная система задач на смеси, растворы и сплавы была апробирована в ходе КПВ по математике в 8 классе в 2016-17 учебном году. Опыт показал, что учащиеся не знавшие вначале, как подойти к решению этих задач, в конце темы успешно заполняли таблицу и получали верный ответ.
Литература:
1.Открытый банк заданий ОГЭ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge;
2. https://oge.sdamgia.ru Каталог заданий. Задачи на проценты, сплавы и смеси
13


























