Современные образовательные технологии на уроках математики

Педагогические технологии на уроках математики

Если человек в школе не научится творить, то и в жизни он будет только подражать и копировать»

Л.Н.Толстой

Подготовила:

учитель математики МОУ «Благодатновская школа» Амвросиевского района ДНР

Бродяная Н.Л.,

специалист высшей категории, «учитель – методист»

Что же такое педагогическая технология?

•   Совокупность приёмов – область педагогического знания, отражающего характеристики глубинных процессов   педагогической   деятельности, особенности их взаимодействия, управление которыми   обеспечивает необходимую эффективность учебно-воспитательного    процесса;

•   Совокупность форм, методов, приёмов и средств передачи социального опыта, а также техническое оснащение этого процесса;

•   Совокупность способов организации учебно-познавательного процесса или последовательность определённых действий, операций, связанных с конкретной деятельностью учителя и направленных на достижение поставленных целей (технологическая цепочка).

В условиях реализации требований ГОС наиболее актуальными становятся технологии:

Информационно – коммуникационная технология

    Технология развития критического мышления

    Проектная технология

    Технология развивающего обучения

    Здоровьесберегающие технологии  

    Технология проблемного обучения

    Игровые технологии

Модульная технология

   Технология мастерских

Кейс – технология

Технология интегрированного обучения

    Технологии уровневой дифференциации  

      Групповые технологии .  

      Традиционные технологии (классно-урочная система)

В условиях реализации требований ГОС наиболее актуальными становятся технологии:

Педагогика сотрудничества.  

1.Уход от традиционного урока через использование в процессе обучения новых технологий позволяет устранить однообразие образовательной среды и монотонность учебного процесса, создаст условия для смены видов деятельности обучающихся

2. Рекомендуется осуществлять выбор технологии в зависимости от предметного содержания, целей урока, уровня подготовленности обучающихся, возможности удовлетворения их образовательных запросов, возрастной категории обучающихся

Современный урок математики должен стать результатом творчества не только учителя, но и учащихся

Достигнуть этой цели можно посредством внедрения в учебный процесс современных педагогических технологий.

Поэтому в основе технологий, применяемых на уроках математики, должен быть заложен принцип высокой мотивации.

Как поддержать у учащихся интерес к изучаемому материалу и активизировать их в течение всего урока, чтобы роль преподавателя состояла не в том, как яснее и красочнее, чем в учебнике сообщить необходимую информацию, а в том, чтобы стать организатором познавательной деятельности, где главное действующее лицо ученик.

Информационно-коммуникативная технология. Использование ИКТ на различных этапах обучения математики

  Информационные технологии, на мой взгляд, могут быть использованы на различных этапах урока математики:

— самостоятельное обучение с отсутствием или отрицанием деятельности учителя;

— частичная замена (фрагментарное, выборочное использование дополнительного материала);

— использование тренинговых (тренировочных) программ;

— использование диагностических и контролирующих материалов;

— выполнение домашних самостоятельных и творческих заданий;

— использование компьютера для вычислений, построения графиков;

— использование программ, имитирующих опыты и лабораторные работы;

— использование игровых и занимательных программ;

- использование информационно-справочных программ.

В

П-Р

Н-Я

Н-Я

С

П-Я

П-Я

M

А

8

Стереометрия

Планиметрия

А

А

а

Н

М

Н

М

Отрезок АН – перпендикуляр

Точка Н – основание перпендикуляра

Отрезок АМ – наклонная

Точка М – основание наклонной

Отрезок МН – проекция

наклонной на прямую а

Отрезок МН – проекция наклонной на плоскость

9

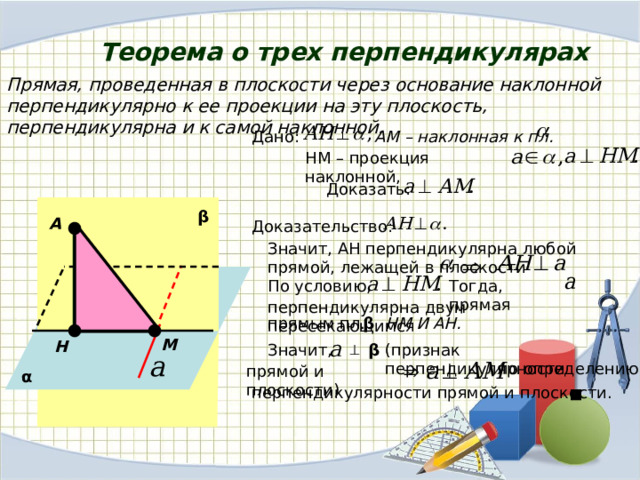
Теорема о трех перпендикулярах

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

АМ – наклонная к пл.

Дано:

НМ – проекция наклонной,

Доказать:

β

А

Доказательство:

Значит, АН перпендикулярна любой прямой, лежащей в плоскости

Тогда, прямая

По условию,

перпендикулярна двум пересекающимся

прямым пл.

НМ И АН.

β

М

Н

(признак перпендикулярности

Значит,

β

по определению

прямой и плоскости)

α

перпендикулярности прямой и плоскости.

Обратная теорема.

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

А

Н-я

П-Р

П-я

Н

М

a

11

Формы использования ИКТ

В процессе преподавания математики, информационные технологии могут использоваться в различных формах. Используемые мною направления можно представить в виде следующих основных блоков:

• мультимедийные сценарии уроков;
• проверка знаний на уроке и дома (самостоятельные работы, математические диктанты, контрольные и самостоятельные работы, онлайн тесты);
• подготовка к ИА

Технология критического мышления

•      Критическое мышление – это способность анализировать информацию с помощью логики и личностно-психологического подхода, с тем, чтобы применять полученные результаты как к стандартным, так и нестандартным ситуациям, вопросам и проблемам.

Этому процессу присуща открытость новым идеям

• 1.     Критическое мышление – мышление самостоятельное
• 2.     Информация является отправным, а не конечным пунктом критического мышления.
• 3.     Критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.
• 4.     Критическое мышление основано на убедительной аргументации.
• 5.       Критическое мышление – мышление социальное

Развитие критического мышления на уроках математики. Задача : воспитание иного ученика, ученика, умеющего работать самостоятельно .

Этапы применения:

• 1 этап – это «Вызов» (мотивация)
• 1 этап – это «Вызов» (мотивация)

Стадия вызова актуализирует имеющиеся знания учащихся, пробуждает интерес к теме. Именно здесь определяются цели изучения материала.

• 2 этап – это «Осмысление»
• 2 этап – это «Осмысление»

Стадия осмысления нового материала (новой информации, идеи, понятия). Здесь происходит основная содержательная работа ученика с текстом. Причем «текст» нужно понимать достаточно широко: это может быть чтение нового материала в учебнике, осмысление условия задачи, речь учителя…

• 3 этап – это «Рефлексия»
• 3 этап – это «Рефлексия»

Стадия размышления или рефлексии. Здесь ученик осмысляет изученный материал и формирует свое личное мнение, отношение к нему .

Все три стадии необходимо на уроке соблюдать, так как это отражает сложный мыслительный процесс

Функции трех фаз технологии развития критического мышления

Действия с положительными и отрицательными числами. Пример из моего урока

• Мотивация урока.

Французский писатель 19 столетия Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы переваривать знания, надо поглощать их с аппетитом». Пусть эти слова послужат девизом сегодняшнего урока, урока-путешествия в страну положительных и отрицательных чисел.

• Осмысление. Повторение изученного материала. Совместная работа в рабочих тетрадях и на доске.

  Тест «Верно, неверно»  Учитель читает, ученики в тетрадях пишут +, -, ?.

  - 5 – отрицательное число.

Расстояние от начала отсчета до точки с координатой -3, равно –3 единицам.

6 – положительное число.

-9 и 9 противоположные числа.

Модуль – 7 равен -7.

0 – положительное число.

5 , то Х – только положительное число? . Рефлексия. Вспомним синквейн на сложение чисел . Сумма (2 чисел) Положительные, отрицательные Одного знака – сложение Разного знака – вычитание Надо запомнить!   А теперь составим синквейн на умножение и деление.   Умножение, деление (2чисел) Положительные, отрицательные Умножать, делить Одного знака– результат положительный Разного знака – результат отрицательный Понятно! " width="640"

Сумма двух отрицательных чисел является отрицательным числом Произведение двух целых положительных чисел равно 0. Произведение двух отрицательных чисел является положительным числом Верно ли, что если Х5 , то Х – только положительное число?

• . Рефлексия. Вспомним синквейн на сложение чисел .
• Сумма (2 чисел)
• Положительные, отрицательные
• Одного знака – сложение
• Разного знака – вычитание
• Надо запомнить!

  А теперь составим синквейн на умножение и деление.

•   Умножение, деление (2чисел)
• Положительные, отрицательные
• Умножать, делить
• Одного знака– результат положительный
• Разного знака – результат отрицательный
• Понятно!

Действия с положительными и отрицательными числами. Пример из моего урока

• Учащиеся по кругу высказываются одним предложением.
• Я научился…
• Было трудно…
• Сегодня я узнал…
• У меня получилось…
• Теперь я могу…
• Далее вопросы учителя:
• Предположите, что будет, если мы будем перемножать не два числа, а больше и среди множителей будут и положительные числа, и отрицательные? Какой будет знак и отчего это зависит?
• Подумайте, какое из заданий для вас было сложным?
• Кто считает, что ему всё-таки нужно доучить или повторить правила?
• У кого после сегодняшнего урока хорошее настроение?

Основные методические приемы развития критического мышления

• Прием «Кластер»,
• таблица,
• учебно-мозговой штурм,
• интеллектуальная разминка,
• зигзаг,
• прием «Инсерт»,
• Эссе,
• Приём «Корзина идей»,

• Приём «Составление синквейнов»,
• метод контрольных вопросов,
• Приём «Знаю../Хочу узнать.…/Узнал…»,
• Круги по воде,
• ролевой проект,
• да - нет,
• приём «Чтение с остановками»

11

Прием «Знаю – Хочу узнать – Узнал»

5-й класс . Тема урока: «Сложение, вычитание обыкновенных дробей»

Прием «Кластер»

• Прием «Кластер» я применяю как на стадии вызова, так и на стадии рефлексии, безусловно, он является способом мотивации к размышлению или до изучения нового материала, или формой систематизации изученной информации при подведении итогов.

Примеры кластеров на моих уроках

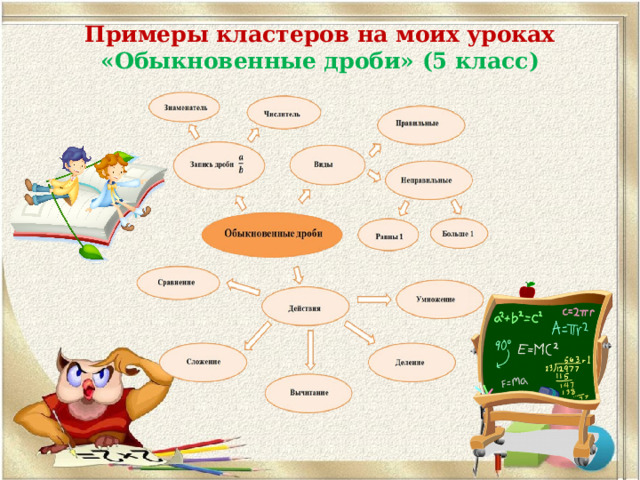
Примеры кластеров на моих уроках «Обыкновенные дроби» (5 класс)

Примеры кластеров на моих уроках «квадратные уравнения» (8 класс)

Примеры кластеров на моих уроках

Примеры кластеров на моих уроках умений по теме «Сложение и вычитание смешанных чисел»

Определение двугранного угла

Теорема о трех перпендикулярах

Определение наклонной

Какие знания и умения необходимы при построении двугранного угла?

Определение проекции

Определение перпендикуляра

Определение пересекающихся плоскостей

Построение пересекающихся плоскостей

Построение перпендикуляра

Примеры кластеров на моих уроках

Примеры кластеров на моих уроках

• "Прямоугольный параллелепипед" - 10 класс

Примеры кластеров на моих уроках

• 7 класс:Треугольники»

Как говорил Цицерон «зажгутся глаза слушающего о глаза говорящего».

• Уроки с применением метода кластера дают ребятам возможность проявить себя, высказать свое видение вопроса, дают свободу творческой деятельности. В целом нетрадиционные технологии, использующиеся в образовательном процессе, повышают мотивацию учащихся, формируют обстановку сотрудничества и воспитывают в детях чувство собственного достоинства, дарят им ощущение творческой свободы.  
• Инновационный подход к обучению позволяет так организовать учебный процесс, что ребёнку урок и в радость, и приносит пользу, не превращаясь просто в забаву или игру. И, может быть, именно на таком уроке, как говорил Цицерон, «зажгутся глаза слушающего о глаза говорящего».

Прием «Синквейн» Правило построения синквейна

Это пятистрочная стихотворная форма, которая помогает описывать суть изучаемых понятий в лаконичной форме, а также осуществлять рефлексию на основе полученных знаний.

• 1 строка – одно существительное, выражающее главную тему cинквейна.
• 2 строка – два прилагательных, выражающих главную мысль.
• 3 строка – три глагола, описывающие действия в рамках темы.
• 4 строка – фраза, несущая определенный смысл.
• 5 строка – заключение в форме существительного (ассоциация с первым словом).

При составлении синквейна, у детей развивается не только критическое мышление, но и образное. Данная форма работы направлена на развитие у учащихся творческих способностей.

Примеры детских синквейнов

• 1. Египетский треугольник. 2. Нужный, точный. 3. Показывает, определяет, помогает 4. Три, четыре и ровно – пять Прямой угол нам отыскать: 5 2 = 4 2 + 3 2 5. Практика!
• 1. Теорема Пифагора 2. Необходимая, важная. 3. Строим, учим, измеряем. 4.Сумму квадратов катетов – мы знаем, Квадрат гипотенузы – вычисляем, Корень квадратный из неё извлекаем И результат - всегда получаем. 5. “Пифагоровы штаны на все стороны равны.

Примеры детских синквейнов

1. Прямые . 1. Контрольная работа . 2. Пересекающиеся, параллельные. 2. Интересная, понятная 3. Строим, проектируем, совмещаем. 3. Пишем, строим, вычисляем 4. Все прямые не имеют ни начала, ни конца. 4. Тетрадь для контрольных работ 5. Это бесконечность! 5. Математика .

1. Смежные углы . 1. Экзамен. 2. Красивы, но не всегда равны. 2.Строгий, трудный. 3. Чертим, измеряем и знаем 3.Проверяет, доказывает, подтверждает 4. Что сумма их равна 180 0 . 4.Что ты знаешь, а чего не знаешь , 5. Теорема. И какую оценку за это получаешь. . 5. Подведение итогов, испытание.

Модульное обучение.

• Принцип: деление изучаемого материала на блоки.
• Формы работы на этапах:

• 1 этап урока – диспут на заданную тему. 2 этап урока – конспект-лекция. 3 этап урока – лекция с обратной связью
• 1 этап урока – диспут на заданную тему.
• 2 этап урока – конспект-лекция.
• 3 этап урока – лекция с обратной связью

ПАРАЛЛЕЛОГРАММ

Признаки параллелограмма

АВ || СD и ВС || СD

АВ || СD и АВ = СD

АВСD – параллелограмм

АВ = СD и АD = ВС

АВСD – параллелограмм

АО = ОС и ВО = ОD

АВСD – параллелограмм

АВСD – параллелограмм

ТРАПЕЦИЯ

Свойства равнобокой трапеции

АВСD – равнобокая трапеция

1) А = D , В = С

2) АС = ВD

3) АВМ = DСN

Признаки равнобокой трапеции. АВСD – трапеция.

Блок - схемы

Блок - схемы

Составь и реши задачу

• 400 кг

• ? – на 53 кг больше, чем

- ? на 33 кг меньше, чем

Технология проблемного обучения

Технологию проблемного обучения использую в основном на уроках: изучения нового материала и первичного закрепления .

Данная технология позволяет :

• активизировать познавательную деятельность учащихся на уроке, что позволяет справляться с большим объемом учебного материала;
• сформировать стойкую учебную мотивацию, а учение с увлечением – это яркий пример здоровьесбережения;
• - использовать полученные навыки организации самостоятельной работы для получения новых знаний из разных источников информации;
• - повысить самооценку учащихся, т. к. при решении проблемы выслушиваются и принимаются во внимание любые мнения .

Тестовые технологии

Задания на тестовой основе получили широкое распространение в моей практике преподавания.

Я их использую на различных этапах урока, при проведении занятий разных типов, в ходе индивидуальной, групповой и фронтальной работы, в сочетании с другими средствами и приемами обучения.

Сегодня существуют разнообразные варианты тестов. Тематические тесты очень удобно проводить после изучения всей темы. В результате тестирования можно увидеть, насколько качественно, полно, осознанно ученик овладел материалом.

На мой взгляд, тесты, созданные самим учителем, позволяют наиболее эффективно выявлять качество знаний, индивидуализировать задания, учитывая особенности каждого ученика и класса.

Тестовые задания составляю с учетом задач урока, специфики изучаемого материала, познавательных возможностей, уровня готовности учащихся

Тестовые технологии

1 Группа.  Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба.

• Задания на тестовой основе получили широкое распространение в моей практике преподавания. Я их использую на различных этапах урока, при проведении занятий разных типов, в ходе индивидуальной, групповой и фронтальной работы, в сочетании с другими средствами и приемами обучения
• Сегодня существуют разнообразные варианты тестов. Тематические тесты очень удобно проводить после изучения всей темы. В результате тестирования можно увидеть, насколько качественно, полно, осознанно ученик овладел материалом.
• Тестовые задания составляю с учетом задач урока, специфики изучаемого материала, познавательных возможностей, уровня готовности учащихся.
• Тесты могут быть направлены на формирование умений и навыков учащихся, на закрепление знаний. Тестовая технология помогает при контроле знаний учащихся.

Игровые технологии .

Игровые технологии способствуют повышению познавательного интереса, развитию мышления; способствуют применению знаний в новой ситуации: являются естественной формой труда ребенка, а также способствуют объединению коллектива и формированию ответственности. Вовлечение обучающихся в игру позволяет достичь эффекта раскрепощения, умения принимать решения, общаться.

Игровые технологии Какие задачи решает использование такой формы обучения:

• Осуществляет более свободные, психологически раскрепощённый контроль знаний.
• Исчезает болезненная реакция учащихся на неудачные ответы.
• Подход к учащимся в обучении становится

более деликатным и дифференцированным.

• Обучение в игре позволяет научить:
• Распознавать, сравнивать, характеризовать, раскрывать понятия, обосновывать, применять

I

Заполни схему:

«Цепочка»

: 10

* 5

+ 34

+ 23

50

81

: 9

ВЫБЕРИ ПЛИТКУ.

Миша Плиткин почти закончил класть новую плитку на пол в ванной. Ему осталось положить всего одну, но тут он заметил, что осталось еще целых четыре. Какую из них ему нужно выбрать?

«Прямоугольная система координат на плоскости» (6 класс)

В результате применения методов игрового обучения достигаются следующие цели:

• стимулируется познавательная деятельность
• активизируется мыслительная деятельность
• самопроизвольно запоминаются сведения
• формируется ассоциативное запоминание
• усиливается мотивация к изучению предмета

Таким образом, дидактическая игра на уроках пополняет, углубляет и расширяет знания, является средством всестороннего развития ребёнка, его умственных, интеллектуальных и творческих способностей, вызывать положительные эмоции, наполнять жизнь коллектива учащихся интересным содержанием, способствовать самоутверждению ребёнка

МЕТОД ГРАФОВ

1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе - семь мостов, расположенных так, как показано на рисунке. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках - проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог.

Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач.

При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он "сжал" сушу в точки, а мосты "вытянул" в линии . Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют  ГРАФОМ .

Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.

Задача на практическое применение графа-дерево.

Построить схему математических объектов , которые изучили семиклассники. С ее помощью проще повторить пройденный материал по геометрии

Решение задач с помощью графов

Задача 1.

Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.

Решение задач с помощью графов

Задача 2.

На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.

Решение:

Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

Здоровьесберегающие технологии.

Здоровьесберегающие технологии (или их элементы) являются обязательным условием при организации учебно-воспитательного процесса в школе. Для повышения работоспособности, предупреждения преждевременного утомления, снятия мышечного напряжения на уроках математики провожу физкультминутки, зарядки для глаз. При проведении урока планирую частую смену видов деятельности (норма 4-7 видов) и их продолжительность (не более 7-10 минут), контроль за правильной рабочей позой.

Считаю, что использование современных образовательных технологий обеспечивает гибкость образовательного процесса, повышает познавательный интерес учащихся, способствует коррекции их недостатков развития, творческой активности. Благодаря внедрению в образовательный процесс современных технологий обучения дети имеют больший шанс приобрести необходимые умения и навыки для дальнейшей жизни и успешной адаптации в обществе, повысить уровень мотивации к обучению.

На сегодняшний день существует достаточно большое количество педагогических технологий обучения, как традиционных, так и инновационных. Нельзя сказать ,что данная система обучения является идеальной.

На сегодняшний день существует достаточно большое количество педагогических технологий обучения, как традиционных, так и инновационных. Нельзя сказать ,что данная система обучения является идеальной.

На мой взгляд, выбор той или иной технологии зависит от многих факторов:  контингента учащихся, их возраста, уровня подготовленности, темы занятия и т.д.

На мой взгляд, выбор той или иной технологии зависит от многих факторов:  контингента учащихся, их возраста, уровня подготовленности, темы занятия и т.д.

Исходя из всего вышесказанного, хочу сказать, что традиционные и  инновационные методы обучения должны быть в постоянной взаимосвязи и дополнять друг друга. Не стоит отказываться от старого и полностью переходить на новое. Следует вспомнить высказывание 

Исходя из всего вышесказанного, хочу сказать, что традиционные и  инновационные методы обучения должны быть в постоянной взаимосвязи и дополнять друг друга. Не стоит отказываться от старого и полностью переходить на новое. Следует вспомнить высказывание 

"Все новое -это хорошо забытое старое."

"Все новое -это хорошо забытое старое."