Способ купцов (исследовательская работа)

МАОУ «Лицей №6» Октябрьского района ГО г.Уфа РБ

Способ купцов

Михайлюк Анна Константиновна,

ученица 7А класса

МАОУ «Лицей №6»

Г. Уфа, РБ

Руководитель:

Тазетдинова Анастасия Николаевна,

учитель математики МАОУ«Лицей №6»

г. Уфа, РБ

Уфа 2016

Содержание

Введение____________________________________________________3

Задачи на смеси и сплавы______________________________________3

Способ купцов_______________________________________________4

Решение задач на смеси и сплавы _______________________________6

Заключение_________________________________________________11

Список литературы___________________________________________12

Введение

Раньше я не любила решать задачи на смеси и сплавы – они казались мне непонятными и запутанными. Так продолжалось до тех пор, пока я не узнала про способ, которым когда-то пользовались купцы. Этот способ мне очень понравился, и я опробовала его на задачах из учебника. Что самое интересное – в интернете есть информация, как решать задачи на смешивание двух компонентов, но я выяснила, что способ купцов «работает» и тогда, когда мы смешиваем три компонента. В своей работе я привожу решение задач на смеси и сплавы традиционным способом и способом купцов.

Задачи:

1. Выяснить, что такое «Способ купцов».

2. Узнать, кто придумал этот удивительный способ.

3. Научиться пользоваться старинным методом.

Предмет изучения:

Применение математических способов при решении задач «На смеси и сплавы».

Объект изучения:

Старинный способ решения задач «Способ купцов».

Гипотеза:

Если мы узнаем, что такое «Способ купцов», то: мы научимся решать задачи «На смеси и сплавы», которые пригодятся нам в жизни.

Я считаю, что эта тема актуальна и в наши дни. Она не только увлекательна и интересна, но и полезна.

Задачи на смеси и сплавы

Нам порой приходится смешивать различные жидкости, порошки, различные твердые или газообразные вещества, а также разбавлять что-либо водой. Задачи на сплавы и смеси входят в учебники, сборники заданий по математике для подготовке к ГИА и ЕГЭ. Чтобы решить подобные задачи необходимо знать следующее:

1.Закон сохранения объема или массы: если два сплава или раствора соединяют в один «новый» сплав или раствор, то V = V1 + V2 – сохраняется объем; и m = m1 + m2 – сохраняется масса.

2. Абсолютное содержание вещества в смеси – это количество вещества, выраженное в единицах измерения (грамм, килограмм, литр и пр.).

3. Относительное содержание вещества в смеси – это отношение абсолютного содержания к общей массе или объему смеси. Часто относительное содержание вещества в смеси называют концентрацией или процентным содержанием. Сумма концентраций всех компонентов смеси равна 1.

Задачи на смеси и сплавы можно разделить на два вида:

• Задается некоторый объем смеси или сплава и от этого объема начинают убирать определенное количество смеси или сплава, а затем добавлять такое же или другое количество смеси или сплава с такой же или другой концентрацией данного вещества. Эта операция может проводиться несколько раз. Такие задачи решаются с помощью уравнений.

• Задаются смеси или сплавы с массами m1, m2, m3… и концентрациями в них некоторого вещества, равными с1, с2, с3…. Требуется определить массу этого вещества в новой смеси или сплаве. Масса вещества в новой смеси или сплаве будет равна

m1c1 + m2c2 + m3c3 + …,

а концентрация c = (m1c1 + m2c2 + m3c3 + …)/(m1 + m2 + m3 + …).

Задачи второго вида можно решить не только с помощью уравнения, но и арифметическим способом, который и называется способом купцов.

Способ купцов

Способ решения, который называется способом купцов, был известен в Европе ещё во времена средневековья. Им пользовались для решения разнообразных задач на смешивание.

Так как этот способ был очень прост, он применялся купцами и ремесленниками при решении практических задач. Но в различных руководствах для мастеров и торговцев никаких обоснованных разъяснений не приводилось. Просто давался рецепт решения: «поступай так и получишь ответ», и словесно описывалась последовательность действий, которые надо выполнить. Эта последовательность называлась тройным правилом.

Тройное правило знали в Древнем Китае и Индии; в средние века оно было одним из основных способов решения арифметических задач. Это правило занимало важное место в программе обучения арифметике в Западной Европе и в России. Оно приводило в восхищение самих составителей арифметических пособий, так, один из авторов русской летописи пишет: «Та строка тройная похвальная и лучшая строка из всех иных строк. Философы её зовут златою строкою».

Задачам подобного типа уделялось большое внимание в старинных рукописях. В 1703 году в России впервые был издан учебник типографским способом (2400 экземпляров), он назывался «Арифметика, сиречь наука числительная». Автором его был Леонтий Филиппович Магницкий. Леонтий Филиппович Теляшин (Магницкий) — русский учёный, педагог. Преподаватель математики. Ему принадлежат множество открытий. Он изучал такие науки, как математика, астрономия, геодезия, навигация. Фамилию Магницкий «жаловал» Леонтию Филипповичу сам Пётр I, в знак почтения и признания его достоинств: «в сравнении того, как магнит привлекает к себе железо, так он природными и самообразованными способностями своими обратил внимание на себя».

На протяжении пятидесяти лет эта книга была основным учебником математики для всех учебных заведений России. Для тех времён эта книга была целой энциклопедией

Рассмотрим задачу из этого учебника:

«Паке аще случится кому иметь штуку сребра весоб токмо един фунт, а была бы она двойного сребра: едино сребро имеет пробу 11, а другое 14, и хотительно есть да будет оная штука пробы 12, и коли кому достоит в той штуке быти лучшему сребру и худшему?»

Сейчас эта задача звучит так:

Имеется два вида серебра, одно 11-й пробы, другое 14-й; сколько надо взять того и другого серебра, чтобы получить фунт серебра 12-й пробы?

Решение с помощью уравнения:

Пусть количество серебра 11-й пробы – X, а количество серебра 14-й пробы – Y.

Составим уравнение:

11X+14Y=12(X+Y)

11X+14Y=12X+12Y

2Y=1X

т.е. на одну часть серебра 11-й пробы нужно взять 2 части серебра 14-й пробы. Следовательно, серебра 14-й пробы - 2/3 от общего количества, а серебра 11-й пробы – 1/3 всего количества.

Теперь рассмотрим решение этой же задачи способом купцов. Для этого представим данные задачи в виде схемы: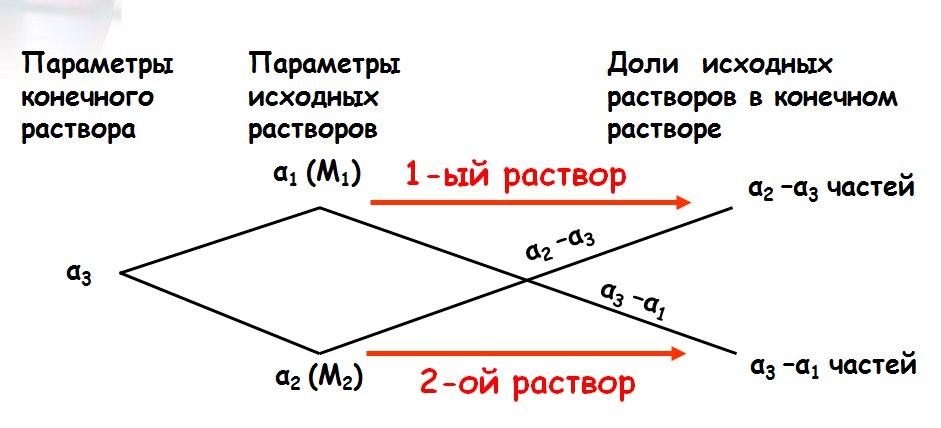

Где:

М1 – масса первого раствора (сплава);
α1 - концентрация первого раствора (сплава);
М2 – масса второго раствора (сплава);

α2- концентрация второго раствора (сплава);
М1+ М2 – масса конечного раствора (сплава);
α3 – концентрация конечного раствора (сплава).

Решение «Способом купцов»

2+1=3 части (всего)

Следовательно:

1/3 – нужно взять серебра 14-й пробы

2/3 – нужно взять серебра 11-й пробы

Решение задач на смеси и сплавы

Задача №1.

При смешивании 5%-ного раствора кислоты, с 40%-ным раствором кислоты получили 140 г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?

Решение «Способом купцов»:

10+25=35 
140:35=4 г
4*10=40 (г) потребуется 7% раствора
4*25=100 (г) потребуется 42% раствора

Задача №2.

В «Занимательной алгебре» Я.И. Перельмана есть любопытная задача под названием «В парикмахерской»:

Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?

- Уж сколько раствора испортили из-за этого!- добавил другой.

- В чем задача?

- У нас имеется два раствора перекиси водорода: 30%- ый 3 % -ый.

Нужно их смешать так, чтобы составился 12% -ый раствор. Не можем подыскать правильной пропорции.

Мне дали бумажку, и требуемая пропорция была найдена.

Она оказалась очень простой. Какой именно?

Решение «Способом купцов»:

Следовательно:
30%-ного раствора надо взять 9%.
А 3%-ного раствора надо взять в два раза больше - 18%.

Задача №3.

Имеется два сорта кислоты: 1сорт – 68%, 2 сорт – 78%. Сколько грамм в сумме нужно взять, чтобы получить 100 г 70% кислоты?

Решение «Способом купцов»

68

8

70

78

2

8+2=10 частей (всего)

68% - 80 грамм нужно взять (8/10 от 100)

78% - 20 грамм нужно взять (2/10 от 100)

Задача №4.

У некоторого человека было 2 сорта масла. 1 сорт – 100 рублей за ведро, другой 60 рублей за ведро. Захотел он продать, смешав их, за 70 рублей за ведро. Какие части этих 2-ух масел нужно взять, чтобы выполнить поставленную цель?

Решение уравнением:

I сорт – X частей.

II сорт – Y частей.

10X + 6Y = 7 (X+Y)

10X + 6Y = 7X+7Y

3X=1Y

То есть X должно быть меньше в 3 раза.

1 часть – дорогого, 3 части – дешевого.

Решение «Способом купцов»:

Значит – 3+1=4 части всего.

3/4 - дешевого.

1/4 - дорогого.

Задача №5.

Сколько нужно взять 4-процентного и сколько нужно взять 10-процентного раствора соли, чтобы получить смесь 6-процентного раствора?

4

4

6

10

2

4+2=6 частей (всего)

Нужно взять 4/6 4-х % раствора.

Нужно взять 2/6 10-и % раствора.

Когда я искала информацию о способе купцов, то узнала, что существуют и другие, похожие, схемы решения задач на смеси и сплавы. К примеру, «Квадрат Пирсона».

Карл Пирсон родился 27 марта 1857 года в Лондоне. Он был разносторонним человеком, активно изучал историю, математику, статистику. Его метод заключается в следующем: строится квадрат и проводятся его диагонали. В левом верхнем углу ставят больший показатель крепости веществ, в левом нижнем углу – меньший. На пересечении диагоналей ставят требуемый показатель крепости. А дальше схема полностью повторяет «Способ купцов». Меня заинтересовала фраза: «У квадрата Пирсона есть недостаток: его можно применять только при смешивании двух растворов». Означает ли это, что с помощью способа купцов можно решить задачу, в которой требуется смешать 3 или более веществ?

Я решила проверить эту догадку, но не смогла найти информацию. Тогда я решила сама проверить, годится ли способ купцов для решения задач подобного рода и нашла подходящие задачи.

Задача №6.

У ювелира имеется серебро 12 пробы, 10 пробы и 6 пробы. Сколько частей серебра каждой пробы нужно взять, чтобы получить серебро 9 пробы?

Здесь необходимы некоторые пояснения: мы можем получить 9-ю пробу лишь путем смешения 12-й и 6-й пробы, либо 10-й и 6-й пробы.

Всего 1+3+3+3=10 частей.

Следовательно:

Серебра 12 пробы - 3 части. Значит 3/10.

Серебра 10 пробы – 3 части. Значит 3/10.

А серебра 6 пробы – 4 части (1+3). Значит 4/10.

Задача №7.

У купца имеется чай трёх сортов: цейлонский – 5 рублей, индийский – 8 рублей, китайский – 12 рублей. Сколько частей каждого сорта надо взять, чтобы получить чай за 6 рублей?

6

5

2

8

1

6+2+1+1=10 частей (всего)

Следовательно:

цейлонского чая нужно взять 8 частей, т.е. 8/10,

индийского чая - 1 часть, т.е. 1/10,

китайского чая - 1 часть, т.е. 1/10.

Я решила проверить, как можно решить эту задачу с помощью уравнения. За х приняла количество цейлонского чая, за у – количество индийского, за р – количество китайского.

Получила уравнение: 5х + 8у + 12р = 6(х + у + р)

5х + 8у + 12р = 6х + 6у + 12р

2у + 6р = х

Уравнения такого типа я решать ещё не умею, поэтому я поступила следующим образом: сама назначала количество одного из чаев. Если задать количество одного чая в смеси, то можно определить количество двух других сортов. Можно также задать количество двух чаев в смеси, тогда однозначно можно определить количество третьего чая. Например: пусть р = 1, у = 2, тогда 5х + 2 · 8 + 1 · 12 = 6(х + 2 + 1)

5х + 28 = 6х + 18

х = 10,

т.е. цейлонского чая нужно взять 10 частей, индийского – 2 части, китайского – 1 часть. Так как это решение отличалось от решения способом купцов, я проверила ещё несколько вариантов:

если у = 1, р = 2, то 5х + 1 · 8 + 2 · 12 = 6(х + 1 + 2)

5х + 32 = 6х + 18

х = 14, т.е. на 14 частей цейлонского чая надо брать 1 часть индийского и 2 части китайского.

Подходит ли ответ, полученный с помощью способа купцов? Чтобы проверить это, я составила уравнение: 5х + 8 + 12 = 6(х + 1 + 1)

5х + 20 = 6х + 12

х = 8.

Таким образом, задачи такого типа имеют несколько решений, а способ купцов даёт одно из них.

Заключение

Таким образом, я решила 8 задач, которые оказались очень простыми, а схема их решения уже давно известна во всем мире. Я убедилась, что с помощью такого метода с лёгкостью можно проверить и решить даже самую сложную задачу. А еще решать задачи таким методом намного проще и интереснее, чем составляя уравнения. С помощью способа купцов можно решить задачи на смешение товаров разной цены, жидкостей с различным содержанием какого-либо вещества, сплавление веществ с разной концентрацией. Этот способ прост и удобен в применении.

Список литературы

1. задачи на смеси - http://viripit.ru/Pag2_1.htm
2. задачи на смеси -https://infourok.ru/zadachi_na_smesi_i_splavy_.-30523..
3. теория способа - https://www.google.ru/search?q=теория+способа+купцов..

4. задачи на смеси – http://matuha.ru/

5. задачи на смеси - http://www.uznateshe.ru/zadachi-na-smesi-i-splavyi/

6. Алгебра 9 класс. Подготовка к ГИА – 2010:учебно-методическое пособие /под ред. Ф. Ф. Лысенко – Ростов-на-Дону:Легион –М.,2009.

12