Тема «Способы задания графов»
План лекции:
-
Реализация графов
-
Задание матрицей инцидентности
-
Задание матрицей смежности
-
Перечислением списком смежности
-
Задание матрицей расстояний
Реализация графов
Человеку удобно работать с графом – рисунком (схемой, диаграммой), так как он может легко установить связь между вершинами в наглядном виде с помощью ребер. Такое геометрическое представление плоского графа называется его реализацией.
Для машинной обработки удобнее задать граф в алгебраической форме – перечислением (списком) ребер и вершин. Но с таким представлением ЭВМ трудно работать, так как для указания каждого ребра нужно еще раз выписывать соответствующую вершину, что плохо с точки зрения сжатия и хранения информации. Иногда граф задается таблицей, состоящей из n строк – вершины, m столбцов – ребер.
Реализация графа – это графическое представление графа.
Способы задания графов:
-
Матрицей инцидентности (таблица);
-
Матрицей смежности (таблица);
-
Списком смежности (перечисление);
-
Матрицей расстояний (таблица).
Задание матрицей инцидентности
МАТРИЦЕЙ ИНЦИДЕНТНОСТИ графа G(V,X) называют прямоугольную матрицу, состоящую из n строк (количество вершин) и m столбцов (количество ребер), в которой:
ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:
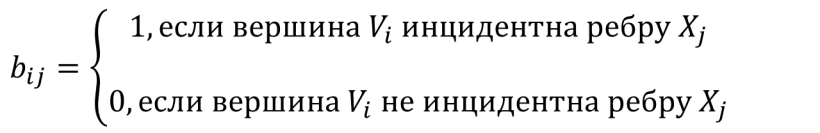
ДЛЯ ОРИЕНТИРОВАННОГО ГРАФА:

Пример: составить для ориентированного графа G1 матрицу инцидентности
|
| r | s | t | u | G1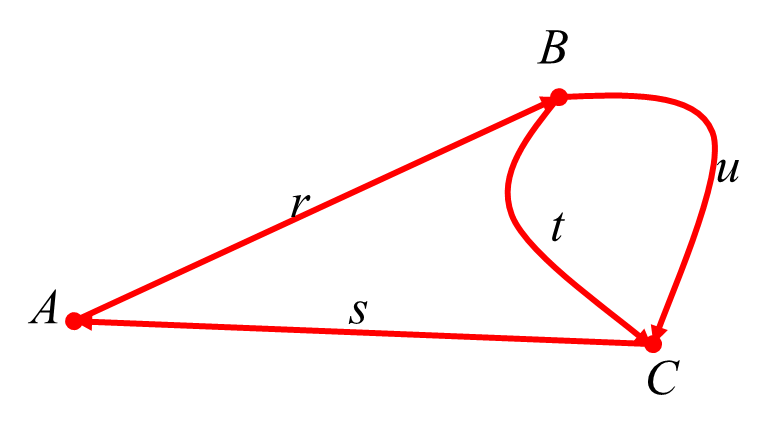 |
| A | 1 | -1 | 0 | 0 |
| B | -1 | 0 | 1 | 1 |
| C | 0 | 1 | -1 | -1 |
Задание матрицей смежности
МАТРИЦЕЙ СМЕЖНОСТИ НЕОРИЕНТИРОВАННОГО ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР называют квадратную матрицу порядка n (количество вершин), в которой:
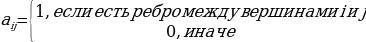
ДЛЯ ОРИЕНТИРОВАННОГО ГРАФА:
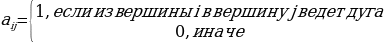
Пример: составить для неориентированного графа G2 матрицу смежности
|
| A | B | C | D | E | G2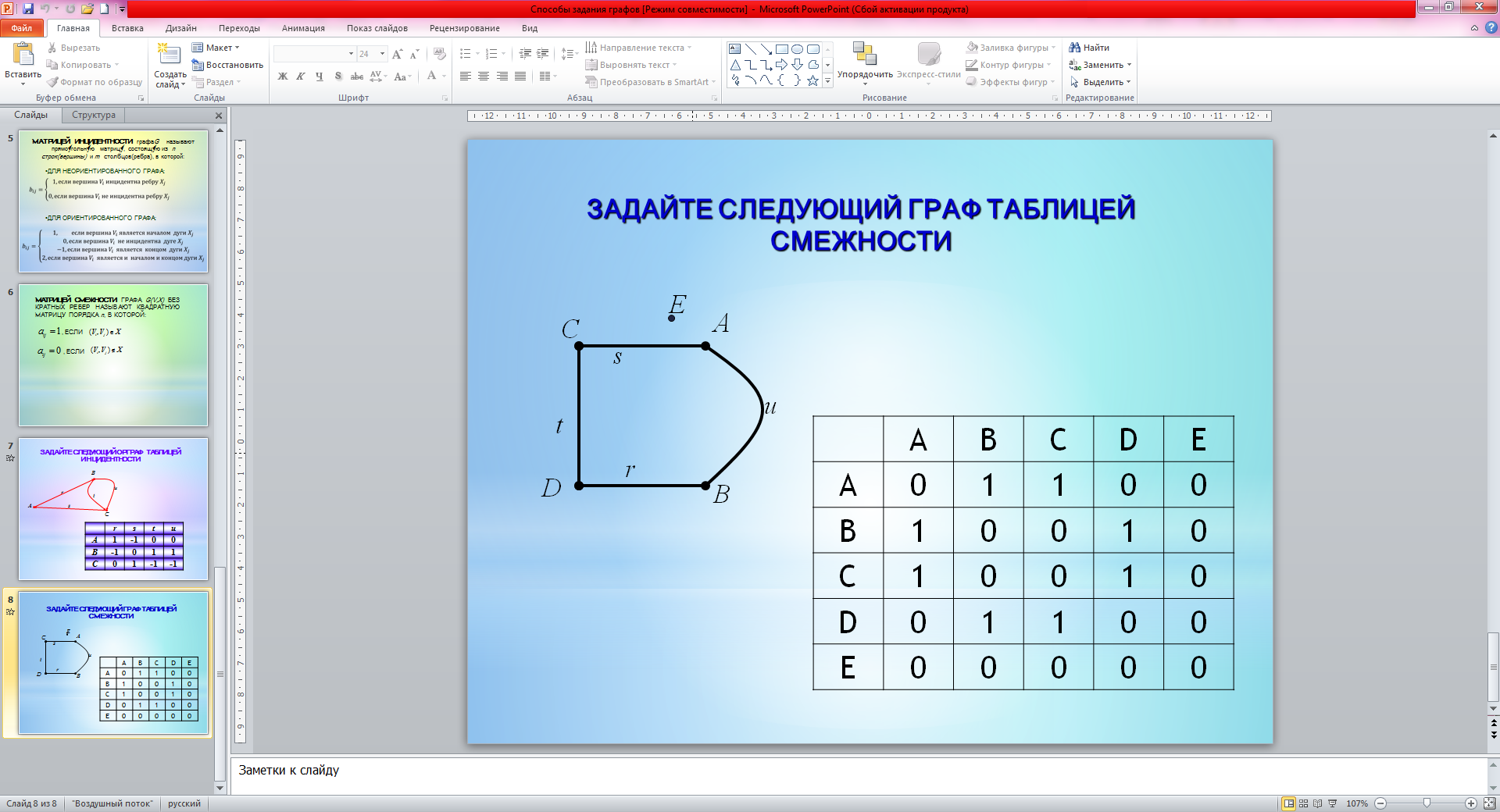 |
| A | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 1 | 0 |
| C | 1 | 0 | 0 | 1 | 0 |
| D | 0 | 1 | 1 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 0 |
Перечислением списком смежности
Список смежности – это список для каждой вершины, в котором отображаются только те, вершины, которые смежные данной.
Пример из предыдущих пунктов,
Список смежности для графа G1 выглядит следующим образом: LA: B, LB: C,C, LC: A.
Список смежности для графа G2 выглядит следующим образом: LA: B,C, LB: D,A, LC: A,D, LD: C,B, LE: -.
Задание матрицей расстояний
МАТРИЦЕЙ РАССТОЯНИЙ графа G(V,X) называют квадратную матрицу порядка n (количество вершин), которая заполняется наименьшим количеством ребер (дуг) находящихся между двумя вершинами (наименьший путь).
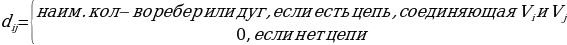
Пример: записать матрицу расстояний для графа G1
|
| А | В | С |
| А | 0 | 1 | 2 |
| В | 2 | 0 | 1 |
| С | 1 | 2 | 0 |
Пример: записать матрицу расстояний для графа G2
|
| А | В | С | D | E |
| А | 0 | 1 | 1 | 2 | 0 |
| В | 1 | 0 | 2 | 1 | 0 |
| С | 1 | 2 | 0 | 1 | 0 |
| D | 2 | 1 | 1 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 0 |
Самостоятельная работа студентов
-
Переписать лекцию в тетрадь и прислать фото
-
Составить для неориентированного графа G2 матрицу инцидентности
-
Составить для ориентированного графа G1 матрицу смежности
-
Построить матрицу расстояний и список смежности для следующих графов:
-
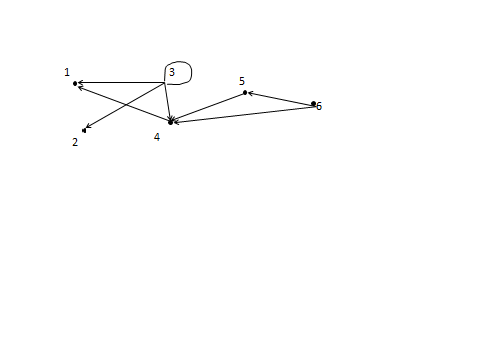 Это ориентированный граф. В вершине 3 петля, добавьте стрелочку. Граф перерисовать.
Это ориентированный граф. В вершине 3 петля, добавьте стрелочку. Граф перерисовать.
-
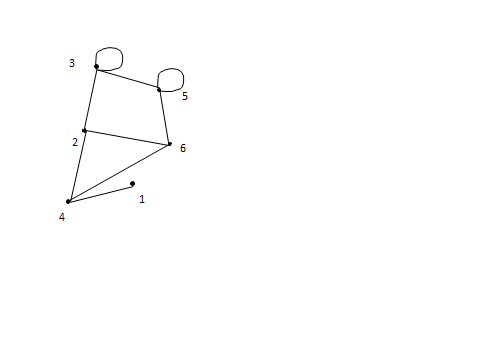 Это неориентированный граф. Граф перерисовать.
Это неориентированный граф. Граф перерисовать.







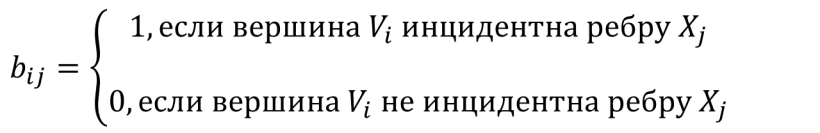


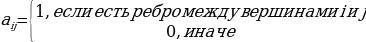
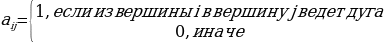

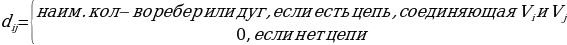
 Это ориентированный граф. В вершине 3 петля, добавьте стрелочку. Граф перерисовать.
Это ориентированный граф. В вершине 3 петля, добавьте стрелочку. Граф перерисовать. Это неориентированный граф. Граф перерисовать.
Это неориентированный граф. Граф перерисовать.




















