Таблица умножения
|
| 1 | 2 |  3 3
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
|  4 4
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Знаки
- больше
≤ - меньше либо равно,
≥ - больше либо равно.
Порядок выполнения действий.
Вычисляем действия в скобках.
Вычисляем степени.
Делаем умножение и деление по порядку, слева на право.
Делаем сложение и вычитание по порядку, слева на право.
Натуральные числа
Числа, применяемые для счета, называются натуральными числами Цифра нуль не относится к натуральным числам. Однозначные числа: 1,2,3,4,5,6,7,8,9
Двузначные: 24,56,и т.д.
Трехзначные: 348,569 и т.д.
Многозначные: 23,562,456789 и т.д.
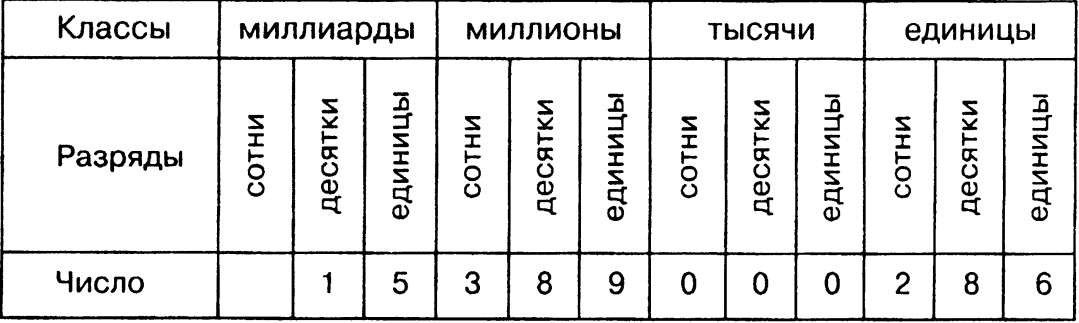
Разбиение числа на группы по 3 цифры, начиная справа, называется классами: первые три цифры – класс единиц, следующие три цифры – класс тысяч, далее миллионы и т.д.
![]() Сумма чисел Разность чисел
Сумма чисел Разность чисел
п + в = с у - в = р
п – первое слагаемое у – уменьшаемое
в – второе слагаемое в – вычитаемое
с – сумма р – разность
![]() Умножение чисел Деление чисел
Умножение чисел Деление чисел
п ∙ в=р д : е=ч
п - первый множитель д - делимое
в - второй множитель е - делитель
р - произведение ч – частное
Решение уравнений
1. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое
x + a = b
x = b – a
2. Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность
x – a = b
x = a + b
3. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
b – x = a
x = b - a
4. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
a · x = b
x = b : a
5. Чтобы найти неизвестное делимое, надо делитель умножить на частное
x : a = b
x = a · b
6. Чтобы найти неизвестный делитель, надо делимое разделить на частное
a : x = b
x = a : b
Соотношения величин
Единицы длины
1см=10мм ; 1м=100см ; 1м=1000мм ;
1дм=10см ; 1дм=100мм ; 1км=1000м ;
1м=10дм ; 1км=10000дм; 1км=100000см;
1км = 1000000мм.
Единицы площади
1см2=100мм2; 1м2=10000см2; 1м2=1000000мм2;
1дм2=100см2; 1дм2=10000мм2; 1км2=1000000м2;
1м2=100дм2; 1га=10000м2;
1ар=100м2; 1км2=100000000дм2;
1км2=100га; 1км2=10000000000см2;
1га=100ар; 1км2=1000000000000мм2.
Единицы массы
1кг=1000г (грамм); 1ц (центнер)=100кг=100000г;
1т (тонна)=1000кг; 1т=10ц=1000кг=1000000г.
Единицы объёма
1литр=1дм3=1000см3; 1см3=1000мм3;
1м3=1000дм3, 1км3=1000000000м3
Схема перевода единиц длины:

км м дм см мм
Схема перевода единиц площади:
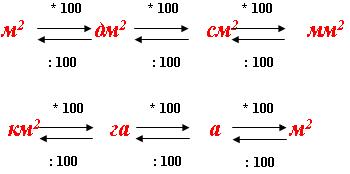
Свойства натуральных чисел.
Свойства сложения:
1. Переместительное a + b = b + a
2. Сочетательное a + (b + c) = (a + b) + c
3. a + 0 = 0 + a = a
Свойства вычитания:
1. Вычитание суммы из числа
a – (b + c) = a – b – c
2. Вычитание числа из суммы
(a + b) – c = a + (b - c)
(a + b) – c = (a - c) + b
3. a – 0 = a
4. a – a = 0
Свойства умножения:
1. Переместительное a ∙ b = b ∙ a
2. Сочетательное a ∙ (b ∙ c) = (a ∙ b) ∙ c
3. Распределительное
(a + b) c = ac + bc
(a - b) c = ac - bc
4. 1 ∙ n = n ∙ 1 = n
5. 0 ∙ n = n ∙ 0 = 0
Свойства деления:
1. a : 1 = a
2. a : a = 1
3. 0 : a = 0
Деление с остатком
Остаток всегда меньше делителя.
Здесь число 23 – делимое, 4 – делитель, 5 – неполное частное и 3 – остаток.
Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка или, иначе, нацело. Чтобы найти делимое a при делении с остатком, надо умножить неполное частное с на делитель b и к полученному произведению прибавить остаток d.
а = с · b + d
Формулы пути
S = V ∙ t ; V = S : t ; t = S : V,
S - это путь (расстояние),
V - это скорость, t – это время.
Фигуры
Периметр – это сумма длин всех сторон.
Прямоугольник – это четырехугольник у которого все углы прямые.

Периметр Р=(а+в)∙2 в
Площадь S=а∙в
 а
а
Треугольник Р=а+в+с а в
с
 Квадрат – это прямоугольник у которого все стороны равны.
Квадрат – это прямоугольник у которого все стороны равны.
Р = 4∙а, S= а∙а =а2 а а
 Прямая - нет начала, нет конца.
Прямая - нет начала, нет конца.

![]()
Луч – есть начало, нет конца.
![]()


Отрезок - есть начало и конец
(ограничен с обоих концов).


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Координатный луч-это луч, у которого есть шкала (одинаковые деления) и указан единичный отрезок.
А Х
1 8
У точки А координата 8, это обозначают так: А(8).
Прямоугольный параллелепипед
У него все грани - прямоугольники.
Его измерения - а,в,с (длина, ширина, высота)
Объём V=а∙в∙с,
Площадь поверхности S=(а∙в+в∙с+а∙с)∙2.
 в а
в а
с
Куб
У куба все грани - квадраты, все стороны равны.
Объём V= а∙а∙а = а3, где а - сторона квадрата.
 Площадь поверхности S= (а∙а+а∙а+а∙а)∙2=6∙а2.
Площадь поверхности S= (а∙а+а∙а+а∙а)∙2=6∙а2.
а
Окружность и круг
Круг - часть плоскости, ограниченная окружностью.
Окружность – линия, которая делит плоскость на две части.
Радиус (r) -это отрезок, соединяющий центр окружности с любой её точкой.
ОА – радиус
Диаметр (d) – отрезок, проходящий через центр и соединяющий две точки окружности.
О
 СК - диаметр С
СК - диаметр С
d= 2*r О
 r
r
А К
Умножение и деление натуральных чисел и его свойства.
Степень числа.
а∙0=0, а∙1=а, а∙а= а2 (читают а в степени 2 или а в квадрате),
а∙а∙а = а3 (читают а в степени 3 или а в кубе), и так далее,
а∙а∙а∙а∙а = а5 (читают а в степени 5)
02=0∙0=0 ноль в любой степени будет ноль,
12=1∙1=1 один в любой степени будет один.
На ноль делить нельзя! а:0=нельзя
а:1=а, а:а=1, а:с+в:с=(а+в):с
Таблица степеней
| число | n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| квадрат | n2 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 |
| куб | n3 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 | 1331 |
| число | n | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| квадрат | n2 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| куб | n3 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |



 Дроби.
Дроби.



 1 числитель
1 числитель
4 знаменатель .
Числитель показывает,
сколько частей взяли, а
знаменатель - на сколько или



 одинаковых частей
одинаковых частей
разделили.
![]()
![]()
![]()
![]()

![]() У правильной дроби
У правильной дроби
числитель меньше, чем 0 ⅟4 1
знаменатель: 5 , 12, 48, 1256 .
6 13 59 189765

![]()
![]()
![]()
![]()
![]()
![]() У неправильной дроби
У неправильной дроби
числитель равен или 0 ⅟4 1 5∕4
больше, чем знаменатель: 5, 12, 48, 1256 .
5 10 9 765
Правильная дробь всегда меньше 1, а неправильная дробь больше
либо равна единице.








 1 4 5 4
1 4 5 4
4 4 , 4 4 .








 5 6 52 12
5 6 52 12
6 6 , 12 12 .
Долю  называют половиной
называют половиной
Долю  называют третью
называют третью
Долю  называют четвертью.
называют четвертью.
Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
Смешанные числа
Сумму 1 +  принято записывать 1
принято записывать 1 , где число 1 – это целая часть, а число
, где число 1 – это целая часть, а число  - его дробная часть.
- его дробная часть.
Чтобы из неправильной дроби выделить целую часть надо:
1) разделить с остатком числитель на знаменатель;
2) неполное частное будет целой частью;
3) остаток (если он есть) дает числитель, а делитель – знаменатель дробной части. Запись числа, содержащую целую и дробную части, называют смешанной.
Чтобы представить число в виде неправильной дроби, нужно:
1) умножить его целую часть на знаменатель дробной части;
2) к полученному произведению прибавить числитель дробной части;
3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.


 5 1 32 2
5 1 32 2
 4 4 , 5 5 .
4 4 , 5 5 .
![]()
![]() _ 5 4 (знаменатель) _ 32 5 (знаменатель)
_ 5 4 (знаменатель) _ 32 5 (знаменатель)
4 1 (целая часть) 30 6 (целая часть)
1 (числитель) 2 (числитель)
Десятичная запись дробных чисел
Числа со знаменателем 10, 100, 1000 и т.д. условились записывать без знаменателя в виде десятичной дроби. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой. Пример: 3,7; 0,125; 5,345.
Сравнение десятичных дробей.
Сравниваем целые части.
Если целые части равны, то начинаем сравнивать соответствующие числа, стоящие после запятой (недостающие – нули).
28,4516,5; 0,9911,3.
Сложение и вычитание десятичных дробей
При сложении (вычитании) десятичных дробей надо:
1) при необходимости уравнять количество знаков после запятой,
добавляя нули к соответствующей дроби.
2) Записать дроби так, чтобы их запятые находились друг под другом.
3) Сложить (вычесть), не обращая внимания на запятую.
4) Поставить запятую в сумме (разности) под запятыми,
складываемых (вычитаемых) дробей.
Запись: 0,6547 = 0,6 + 0,05 + 0,004 + 0,0007 называют разложением данного числа по разрядам.
Приближенные значения чисел. Округление чисел
Если а
При округлении чисел:
Если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.
Если первая отброшенная или замененная нулем цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения.
Пример:
Округлим до десятых: 123,25≈123,30=123,3; 1,21≈1,2; 0,02≈0,00=0; 56,76556≈56,80000=56,8.
Округлим до десятков: 123,25≈120,00=120; 6,21≈10,00=10; 0,02≈00,00=0; 56,76556≈60,00000=60.
До сотых: 56,6789≈56,6800=56,68; 0,0235≈0,0200=0,02.
Умножение десятичных дробей на натуральные числа
Чтобы умножить десятичную дробь на натуральное число, надо:
1) умножить ее на это натуральное число, не обращая внимания на запятую;
2) в полученном произведении отделить запятой столько цифр, сколько их отделено запятой в десятичной дроби.
Чтобы умножить десятичную дробь на 10,100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы. 8,5 · 1000 = 8500
Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда закончится деление целой части.
При делении десятичной дроби на 10 , 100 , 1000 , ... , надо перенести запятую в этой дроби влево на столько знаков, сколько нулей в делителе.
Например:
34,9 : 10 = 3,49 ; 746 : 100 = 7,46 ; 28,1 : 1000 = 0,0281 .
Умножение десятичных дробей
Умножить число на 0,1; 0,01; 0,001 и т.д. – то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого надо перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.
Чтобы перемножить две десятичные дроби, надо:
1) Выполнить умножение, не обращая внимания на запятые;
2) отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей. При умножении числа на неправильную десятичную дробь оно увеличивается или не изменяется. При умножении числа на правильную десятичную дробь оно уменьшается.
Деление на десятичную дробь
Чтобы разделить число на десятичную дробь, надо:
1) в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на натуральное число.
При делении числа на неправильную дробь, это число уменьшается, а при делении на правильную дробь оно увеличивается.
Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо перенести запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей (то есть умножить ее на 10, 100, 1000 и т.д.). Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей. 56,87 : 0,0001 = 56,8700 : 0,0001 = 568 700
Разряды.
| Целая часть |
| Дробная часть |
| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | , | 1 | 2 | 3 | 4 | 5 |
| единицы миллиардов | сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы |
| десятые | сотые | тысячные | десятитысячные | сотни тысячных |
Среднее арифметическое
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Ср. ар. = (сумма чисел) : (количество слагаемых)
Сумма чисел = (среднее арифметическое) * (количество чисел)
Средняя скорость движения:
Ср.скорость = (весь пройденный путь) : (все время движения)
Проценты
Процентом называют одну сотую часть. Процент обозначают знаком %.
Так как 1% равен сотой части величины, то вся величина равна 100%.
Чтобы обратить десятичную дробь в проценты, надо ее умножить на 100. 0,35 = 35%
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100. 40% = 0,4
Углы.(измеряем в градусах транспортиром.)
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки.
Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят – вершиной угла.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой: ∟АОВ или ∟О.

Острый угол меньше прямого угла.

![]()
Прямой угол равен 90⁰.
![]()

 Тупой угол больше 90⁰.
Тупой угол больше 90⁰.
![]() ● Развернутый угол равен 180⁰.
● Развернутый угол равен 180⁰.
Измеряют углы с помощью транспортира.



С
135⁰
 0⁰ 180⁰
0⁰ 180⁰

![]() А В
А В
L ABC = 135⁰.







 3
3 4
4




 а
а Квадрат – это прямоугольник у которого все стороны равны.
Квадрат – это прямоугольник у которого все стороны равны.  Прямая - нет начала, нет конца.
Прямая - нет начала, нет конца. 











