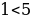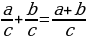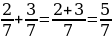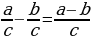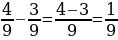Просмотр содержимого документа
«Справочные материалы по математике 5 класс (на стенд)»
ШКАЛЫ И КООРДИНАТЫ
Деления на линейке, термометре, весах и т.д.
образуют шкалу.
А В


 Длина отрезка АВ равна 5 см.
Длина отрезка АВ равна 5 см.
Деление
термометра - 5˚C
Термометр
показывает 25˚C
O A x





 0 1 2 3 4 5
0 1 2 3 4 5
Бесконечная шкала Ox называется координатной прямой. Точка A имеет координату 4, пишут A(4).
РЕШЕНИЕ УРАВНЕНИЙ
Уравнение – равенство, которое содержит неизвестную букву.

Пример:
2x + 5 = 7
Значение буквы, при котором уравнение превращается в верное числовое равенство, называется корнем уравнения.
x = 1 - корень уравнения 2x + 5 = 7, так как
2 * 1 + 5 = 7 – верное равенство.


Примеры:
Решить уравнение – означает найти все его корни.
1) 3x - 12 = 15 2) (x + 3) * 5 = 25 3) 2x + x = 15
3x = 15 + 12 (x + 3) = 25 : 5 3x = 15
3x = 27 x + 3 = 5 x = 15 : 3
x = 27 : 3 x = 5 – 3 x = 5
x = 9 x = 2 Ответ: x = 5.
Ответ: x = 9. Ответ: x = 2.

ОБЫКНОВЕННАЯ ДРОБЬ. СРАВНЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
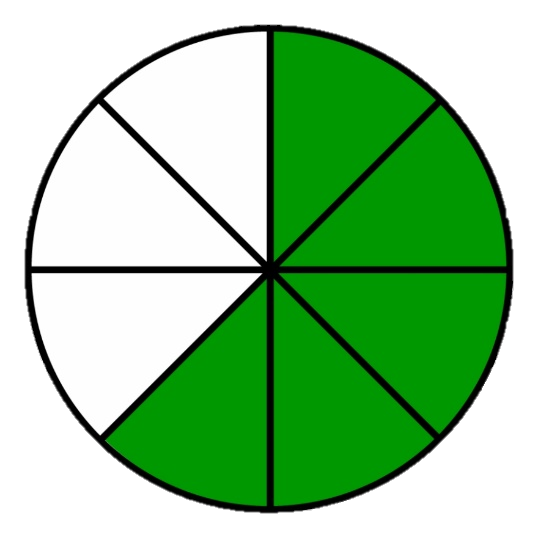
5 долей из 8 — это дробь 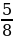 .
.
5 — числитель дроби (сколько долей взято)
8 — знаменатель дроби (сколько долей взято)

Пример:
Дроби можно изображать на координатной прямой 






0 
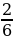
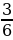
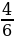
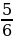 1
1


Пример:
Сравнение дробей с одинаковым знаменателем: из двух дробей с одинаковым знаменателем меньше та дробь, числитель которой меньше.

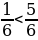 , так как
, так как 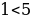
| СВОЙСТВА СЛОЖЕНИЯ | СВОЙСТВА ВЫЧИТАНИЯ |
|
| Переместительное свойство: a + b = b + a | Свойство вычитания суммы из числа: a - (b + с) = a - b - c |
|
| Сочетательное свойство: a + (b + с) = (a + b) + c | Свойство вычитания числа из суммы: (a + b) - с = (b – с) + a |
|
| Свойство нуля: a + 0 = a | Свойство нуля: a - a = 0 |
|
| СВОЙСТВА УМНОЖЕНИЯ |
|
| Переместительное свойство: a * b = b * a | Сочетательное свойство: (a * b) * c = a * (b * с) |
|
| Распределительное свойство: (a + b) * с = a * c + b * c (a - b) * с = a * c - b * c |
|
| Свойство единицы: a * 1 = a | Свойство нуля: a * 0 = 0 |
|
| РАСПРЕДЕЛИТЕЛЬНЫЕ СВОЙСТВА ДЕЛЕНИЯ |
|
| (a + b) : с = a : c + b : c | (a - b) : с = a : c - b : c |
|
| (a * b) : с = (a : c) * b = (b : c) * a a : (b * с) = (a : b) : c = (a : c) : b |
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Правило сложения дробей
с одинаковыми знаменателями:

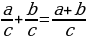
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же:

Пример:

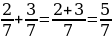
Правило вычитания дробей
с одинаковыми знаменателями:

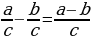
Чтобы из одной дроби вычесть другую дробь с тем же знаменателем, из числителя
уменьшаемого вычесть числитель
вычитаемого, а знаменатель оставить тот же:

Пример:

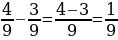
ТАБЛИЦА СТЕПЕНЕЙ
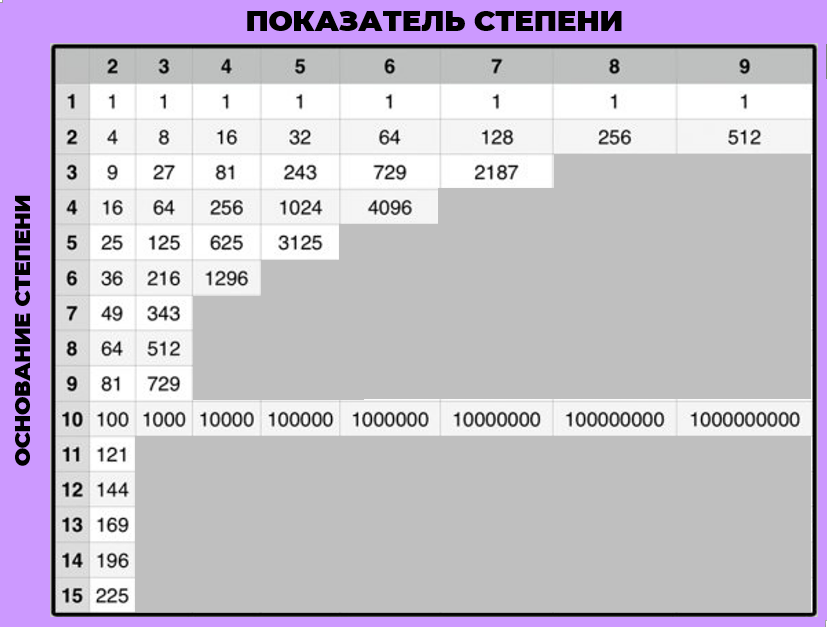
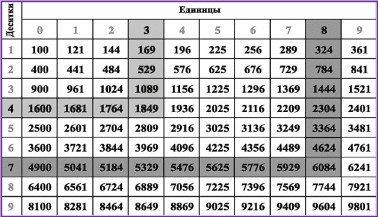
ТАБЛИЦА КВАДРАТОВ ОТ 10 ДО 99








 Длина отрезка АВ равна 5 см.
Длина отрезка АВ равна 5 см.




 0 1 2 3 4 5
0 1 2 3 4 5



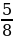 .
.



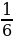
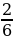
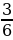
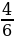
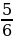 1
1


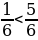 , так как
, так как