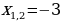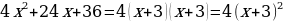| Если в уравнение переменная входит в виде некоторой функции от одного и того же выражения, то, как правило, обычно удобно это одинаковое выражение с переменной обозначить одной буквой (новой переменной) |
| 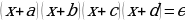
| Перегруппировать сомножители так (если возможно), чтобы выполнялось равенство 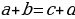 , , И попарно раскрыть скобки | 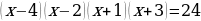
Решение. Перепишем уравнение таким образом: 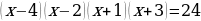
(тогда -4+3=-2+1) и раскроем скобки. Замена 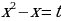 дает уравнение дает уравнение 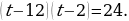 Тогда Тогда 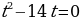
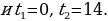
Обратная замена дает уравнение 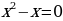 или или 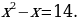 Отсюда Отсюда 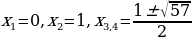 |
| Возвратное уравнение Уравнение вида f(x)=0, Где f(x)- многочлен стандартного вида, у которого равны коэффициенты членов, одинаково удаленных от начала и конца уравнения | Уравнение четной степени делим на степень среднего члена и группируем члены с одинаковыми коэффициентами. Уравнение нечетной степени всегда имеет корень 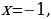 делим его на делим его на 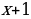 (получаем возвратное уравнение четной степени) (получаем возвратное уравнение четной степени) | 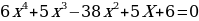
Решение. Это возвратное уравнение четной степени. Так как 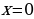 не является его решением, то, разделив обе части на не является его решением, то, разделив обе части на 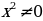 (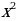 - степень с переменной среднего члена), получим уравнение, равносильное данному. - степень с переменной среднего члена), получим уравнение, равносильное данному. Группируя члены с одинаковыми коэффициентами, получаем уравнение 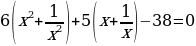 , решения которого приведены выше , решения которого приведены выше |







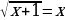
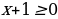 , т.е.
, т.е. 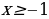
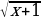 определяется условием
определяется условием 
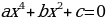
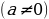
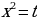
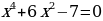
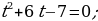
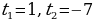
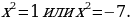
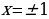
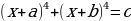
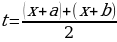
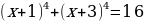
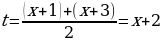
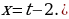
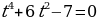 .
.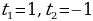
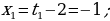
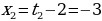
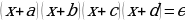
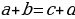 ,
,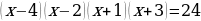
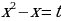 дает уравнение
дает уравнение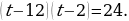 Тогда
Тогда 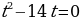
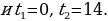
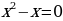 или
или 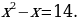 Отсюда
Отсюда 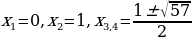
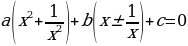
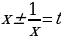
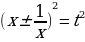 и отсюда
и отсюда 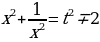
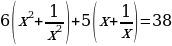
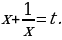 Тогда
Тогда 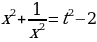
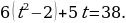
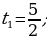
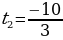 . Решая эти уравнения, получаем
. Решая эти уравнения, получаем 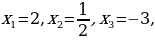
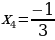
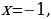 делим его на
делим его на 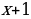 (получаем возвратное уравнение четной степени)
(получаем возвратное уравнение четной степени)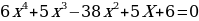
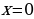 не является его решением, то, разделив обе части на
не является его решением, то, разделив обе части на 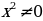
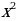 - степень с переменной среднего члена), получим уравнение, равносильное данному.
- степень с переменной среднего члена), получим уравнение, равносильное данному.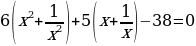 , решения которого приведены выше
, решения которого приведены выше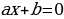 , где a и b – действительные числа.
, где a и b – действительные числа.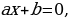 тогда
тогда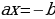
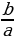
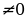
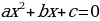 , где a, b, c – некоторые числа, причем а≠0, называют квадратным
, где a, b, c – некоторые числа, причем а≠0, называют квадратным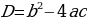 - дискрминант
- дискрминант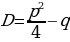 – дискриминант приведенного уравнения
– дискриминант приведенного уравнения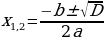
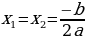
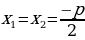
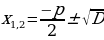 , два различных корня
, два различных корня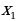 и
и 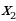 – корни квадратного уравнения
– корни квадратного уравнения 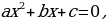 то
то 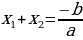
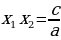
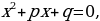 то
то 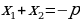
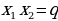
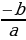 , а произведение равно
, а произведение равно 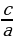 , то эти числа являются корнями квадратного уравнения
, то эти числа являются корнями квадратного уравнения 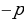 , а произведение равно
, а произведение равно 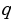 , то эти числа являются корнями приведенного квадратного уравнения
, то эти числа являются корнями приведенного квадратного уравнения 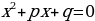
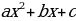 , то
, то 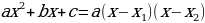
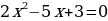 при
при 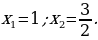
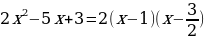
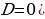 , то
, то 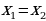 и тогда
и тогда 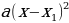 при
при 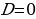
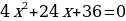 при
при