
Открытый урок
по статистике
Средние величины в статистике.
Средняя арифметическая
Разработала
преподаватель
специальных дисциплин
Зотова Н.Н .
Алматы 2017

«Статистика знает всё» , - утверждали Ильф и Петров в своем знаменитом романе «Двенадцать стульев» и продолжали :
«Известно, сколько какой пищи съедает в год средний гражданин республики...
Известно, сколько в стране охотников, балерин... станков, велосипедов, памятников, маяков и швейных машинок...
Как много жизни, полной
пыла, страстей и мысли,
глядит на нас
со статистических таблиц!..»

Повторение –
мать учения
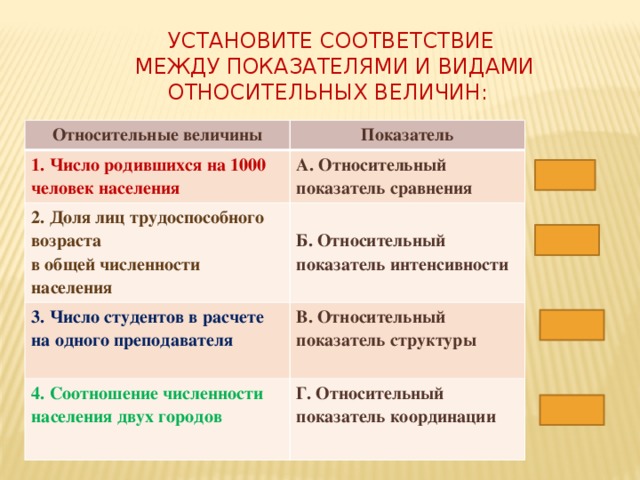
Установите соответствие между показателями и видами относительных величин:
Относительные величины
Показатель
1. Число родившихся на 1000 человек населения
А. Относительный показатель сравнения
2. Доля лиц трудоспособного возраста
3. Число студентов в расчете на одного преподавателя
в общей численности населения
В. Относительный показатель структуры
Б. Относительный показатель интенсивности
4. Соотношение численности населения двух городов
Г. Относительный показатель координации
Г
В
Б
А

Абсолютные показатели
могут выражаться
А) в натуральных единицах измерения;
Б) в процентах;
В) в условно – натуральных единицах измерения;
Г) в д енежных единицах измерения;
Д) в виде простого кратного отношения
(в виде коэффициентов);
Е) в трудовых единицах измере ния.

Показатели, выражающие размеры, объем,
уровни социально-экономических
явлений и процессов,
являются величинами
А) Абсолютными;
Б) Относительными

Относительные величины получаются в результате:
А) сложения индивидуальных абсолютных величин
Б) подсчета числа единиц, входящих в каждую группу или совокупность в целом;
В) деления одного абсолютного показателя на другой

О тносительные статистические показатели могут выражаться
А) в виде простого кратного отношения;
Б) в процентах;
Г) в трудовых единицах измерения
Д) в виде условно-натуральных единицах измерения;
Е) в денежных единицах измерения.

ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧИНЫ
Средняя величина - обобщенная количественная характеристика признака в однородной статистической совокупности в конкретных условиях места и времени (характеристика уровня цен, заработной платы, основного капитала, численности населения и др.).

Сущность средней
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака некоторой уравновешенной средней величиной .

Ученые о средних величинах
Английский экономист
В. Петти (1623—1687 гг.) широко использовал средние величины.
Он хотел использовать их
в качестве меры стоимости расходов на среднее дневное пропитание одного работника.

Бельгийский статистик А. Кетле
(1796—1874 гг.) выразил взгляды на среднюю величину в своей теории среднего человека.
Средний человек – это человек, обладающий всеми качествами в среднем размере
средняя смертность или рождаемость, средний рост и вес,
средняя быстрота бега,
средняя наклонность
к браку и самоубийству,
к добрым делам и т. д.).
Для А. Кетле
средний человек
– это идеал человека

Английский статистик
А. Боули (1869– 1957гг.) – один из самых видных теоретиков новейшего времени в области теории средних величин. А. Боули рассматривает средние величины лишь с количественной стороны, тем самым отрывает количество от качества.

К. Маркс утверждал,
что в средней величине погашаются индивидуальные отклонения от общего уровня и средний уровень становится обобщающей характеристикой массового явления

Применение
Плановые расчеты
Прогнозные расчеты
Финансовые расчеты

Средняя для некоторых экономических показателей
Средняя цена
Стоимость реализованного товара
реализованного=
товара
Количество реализованного товара
Средняя
Затраты на производство продукции
себестоимость =
продукции
Количество произведённой продукции
Средняя
Фонд заработной платы
заработная
=
плата
работающих
Количество
Ф
актически достигнутый показатель
Средний
процент
=
выполнения плана
Запланированный показатель

Виды средних показателей
Средние
Структурные
Степенные
- Геометрическая
- Квадратическая
- Гармоническая
- Арифметическая
16

Средняя арифметическая простая используется в тех случаях, когда варианты или варьирующие признаки встречаются только по одному разу и имеют одинаковый вес в совокупности.
Средняя арифметическая взвешенная используется,
когда данные сгруппированы,
а отдельные значения признака встречаются неодинаковое число раз.

Пример 1.
Имеются следующие данные о заработной плате рабочих
Табельный номер рабочего
1
Заработная плата, (тенге)
103000
2
3
125000
4
94000
5
93500
107000
6
7
82500
8
84200
9
93700
10
72200
102500
Обозначив заработную плату через x , определим сумму заработной платы всех 10 рабочих, тогда
где n – число значений x , равное числу рабочих бригады .
тенге

Пример 2.
Имеются следующие данные:
№ бригады
1
Число рабочих
Заработная плата одного рабочего (тенге)
2
10
12
97000
89000
Определить среднюю заработную плату рабочего по 2 бригадам
Исходя из имеющихся данных фонд заработной платы по каждой
бригаде определим путем умножения заработной платы одного
рабочего ( x ) на число рабочих( f ) , а по двум бригадам вместе
как сумму
, тогда
тенге

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака.
Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности,
а произведение этих единиц
на значения признака
(то есть М=х*f).

Пример 3. Имеются следующие данные
№ бригады
1
Заработная плата одного рабочего, д.е.
Фонд заработной платы, д.е.
2
93000
83500
930000
1252500
Помня, фонд заработной платы является произведением заработной платы одного рабочего на количество рабочих,
для расчета средней заработной платы используется
формула средней гармонической
:
Тогда
тенге

Средняя геометрическая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

Задача 1. На колледжной спартакиаде проводится несколько квалификационных
забегов на 100 метров, вот их результаты.
15,5; 16,8; 21,8; 18,4; 16,2; 32,3; 19,9; 15,5; 14,7; 19,8; 20,5; 15,4.
Среднее арифметическое равно:
18.9
Задача 2. . Две автомашины прошли один и тот же путь (240 км): одна со скоростью 60 км/ч, другая – 80 км/ч. Определите среднюю скорость автомашины
68,6
Задача 3. Какую величину выигрыша можно считать средней, если максимальный размер выигрыша – 1 млн.тенге., а минимальный –
100 тенге.?
500 050
Задача 4. На основе приведенных данных вычислите среднюю цену хлеба.
Наименование
Объем продажи (кг)
Хлеб «Бородинский»
Цена (тг.)
100
Хлеб «Формовой»
150
80
60
68
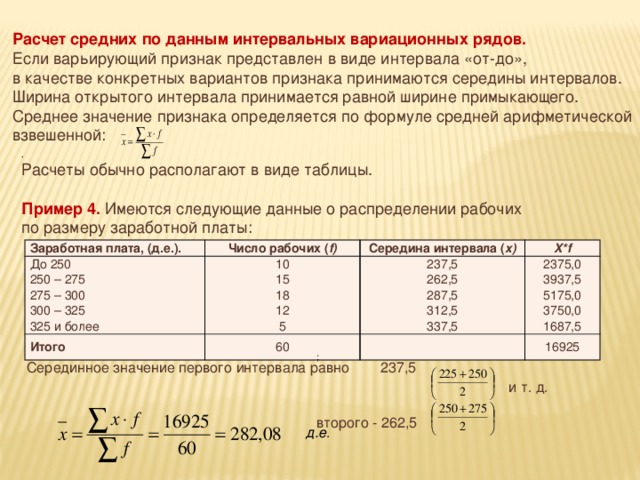
Расчет средних по данным интервальных вариационных рядов.
Если варьирующий признак представлен в виде интервала «от-до»,
в качестве конкретных вариантов признака принимаются середины интервалов.
Ширина открытого интервала принимается равной ширине примыкающего.
Среднее значение признака определяется по формуле средней арифметической
взвешенной:
.
Расчеты обычно располагают в виде таблицы.
Пример 4. Имеются следующие данные о распределении рабочих по размеру заработной платы:
Заработная плата, (д.е.).
Число рабочих ( f)
До 250
Середина интервала ( x)
Итого
250 – 275
10
X*f
60
237,5
275 – 300
15
2375,0
300 – 325
18
262,5
325 и более
16925
12
3937,5
287,5
5175,0
5
312,5
3750,0
337,5
1687,5
;
второго - 262,5
Серединное значение первого интервала равно 237,5
и т. д.
д.е .
Свойства средней арифметической
Первое свойство . Сумма отклонений индивидуальных значений признака от их средней арифметической величины равна нулю.
Это свойство средней может быть использовано, в частности, для контроля правильности вычислений арифметической средней: если средняя вычислена правильно, сумма отклонений должна равняться нулю (практически, с учетом округлений, допускаемых при вычислении средней - очень близка к нулю).
Второе свойство . Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшиться во столько же раз.
Вследствие этого свойства индивидуальные значения признака можно сократить в n раз, произвести расчет средней и результат умножить на n. Возможно использовать, если, например, заработная плата всех работников фирмы увеличилась на 10% (увеличилась в 1.1 раза), то и средняя заработная плата работников фирмы увеличилась на 10%.
Третье свойство. Если к каждому индивидуальному значению признака прибавить или вычесть постоянное число, то средняя величина увеличится (или уменьшится) на это же число.
Можно использовать, если, например, цена на товар увеличилась на 500 тенге вследствие увеличения процентной ставки фирмы-продавца, следовательно и средняя стоимость товара увеличится на 500 тенге.
Четвертое свойство. Если все веса средней (частоты f) одинаково увеличить (или уменьшить) в несколько раз, средняя арифметическая не изменится.
Увеличение всех весов в несколько раз приводит к тому, что во столько же одновременно увеличится и числитель, и знаменатель дроби (средней арифметической), поэтому значение дроби не изменяется.
Пятое свойство. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа.

Когда нужно и не нужно
среднее арифметическое?
(варианты ответов студентов):
Сравнение уровня зарплат в различных отраслях экономики, температуру и уровень осадков на одной и той же территории за сопоставимые периоды времени, урожайность выращиваемых культур в разных географических регионах и т. д.
Вычисление средних трат в семье на продукты, средней урожайности картофеля на огороде, средних расходов на продукты, чтобы понять, как поступать в следующий раз, чтобы не было большого перерасхода, средней оценки за семестр – по ней поставят оценку за год.
НО !
Нет смысла вычислять среднюю зарплату моей мамы и главы администрации президента, среднюю температуру здорового и больного человека, средний размер обуви у меня и у моего брата.

Немного юмора
(высказывания о статистике):
Статистика - наука, занимающаяся изготовлением
недостоверных фактов из достоверных цифр
(Эван Эсари)
Статистика может доказать что угодно, даже правду
(Ноэл Мойнихан)
Статистика - это наука о том, сколько всего приходится на каждого человека, если бы все делились справедливо. (Константин Мелихан)
Статистики как судебные психиатры –
они могут подтвердить правоту обеих сторон
(Фиорелло Да Тардиа)
Не принимай на веру того, что говорит статистика,
пока тщательно не изучишь, о чем она умалчивает
(Уильям Уотт)
Статистика, пожалуй, это самая божественная из наук. Ведь она переводит любое событие из разряда случайного
в разряд закономерного.
Для политиков статистика - меч, для бюрократов - щит.
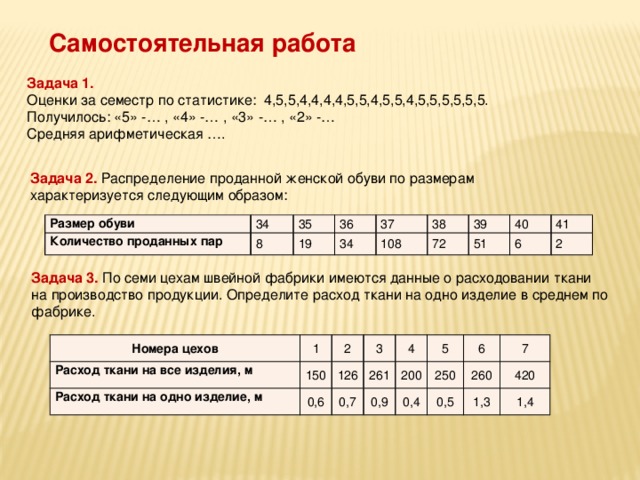
Самостоятельная работа
Задача 1.
Оценки за семестр по статистике: 4,5,5,4,4,4,4,5,5,4,5,5,4,5,5,5,5,5,5.
Получилось: «5» -… , «4» -… , «3» -… , «2» -…
Средняя арифметическая ….
Задача 2. Распределение проданной женской обуви по размерам
характеризуется следующим образом:
Размер обуви
Количество проданных пар
34
8
35
19
36
37
34
108
38
72
39
51
40
6
41
2
Задача 3. По семи цехам швейной фабрики имеются данные о расходовании ткани
на производство продукции. Определите расход ткани на одно изделие в среднем по фабрике.
Номера цехов
Расход ткани на все изделия, м
1
Расход ткани на одно изделие, м
2
150
3
126
0,6
4
261
0,7
5
200
0,9
0,4
6
250
7
0,5
260
1,3
420
1,4

Задача 4 . Распределение рабочих по стажу работы
характеризуется следующими данными.
Стаж работы, лет
Число рабочих, чел.
до 2
4
2-4
23
4-6
20
6-8
8-10
35
11
10 и более
7
Итого
100

Домашнее задание
1. Изучить тему
2. Сделать презентацию на тему «Значение средних величин в экономике, привести примеры»
3. Решить задачу
Известна выработка рабочих трех строительных бригад
.
Номер рабочего
Дневная выработка рабочего, шт.
1-я бригада
1
2-я бригада
35
2
3-я бригада
32
38
3
4
36
34
40
35
42
33
5
6
36
34
41
33
45
35
7
40
–
33
43
30
41
Определите среднее число деталей, обрабатываемых одним рабочим в день:
1) для каждой бригады, дайте сравнительную характеристику этих средних;
2) для всех бригад в целом;
3) ответьте на вопрос, как изменится среднедневная выработка рабочего по каждой бригаде, если все индивидуальные значения выработки:
а) увеличить на 5 единиц;
б) уменьшить на 5 единиц;
в) увеличить в два раза;
г) уменьшить в два раза .

Обобщение
изученного материала
Средняя должна характеризовать качественно однородную совокупность;
Средние должны исчисляться по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально-экономические явления .
Далеко не всегда имеет смысл вычислять среднюю,
т.к. во многих ситуациях
это может не иметь никакого содержательного смысла

Подведение итогов
В заключение нашего урока ответьте,
пожалуйста, на следующие вопросы:
Что тебе больше сего понравилось? ______________
Что тебе меньше всего понравилось? _____________
Я узнал(а) _____________________________________
Еще я хотел(а) бы узнать ________________________

Используемые сайты
http://fb.ru/article/108141/mediana-v-statistike-ponyatie-svoystva-i-raschet
http://fb.ru/article/108141/mediana-v-statistike-ponyatie-svoystva-i-raschet#image239723
http://ramki-vsem.ru/kliparty-zhivotnye.html
( http://nirvana.tomsk.ru/dictionary?id=9&word=%EC%E5%E4%E8%E0%ED%E0/ )

Спасибо за внимание!
Успехов
в приобретении
знаний!







 , где
, где  тенге
тенге , тогда
, тогда тенге
тенге тенге
тенге  .
.
 ;
; и т. д.
и т. д. д.е.
д.е.











































