Магия чисел и симметрия фигур
Понятие «симметрия» встречается в философии и искусстве, в науке и обиходной речи.
Симметрия есть идея,-утверждал математик Г. Вейль,-с помощью которой человек в течении веков пытался объяснить и порядок , и красоту, и совершенство.
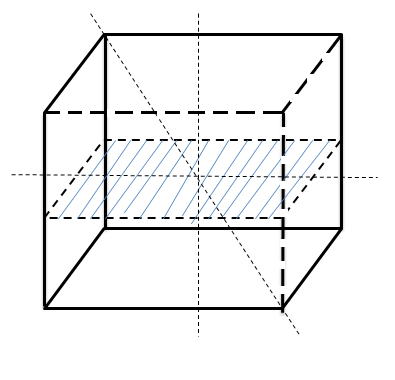
Симметрия обычно связывают с геометрией, с фигурой. Так, говорят, что равнобедренный треугольник имеет одну ось симметрии, правильный треугольник-три оси , правильный четырехугольник (квадрат) – четыре оси, правильный шестигранник (куб) имеет тринадцать осей симметрии и девять плоскостей симметрии (на рисунке 1 указаны лишь некоторые из них).
1

Великим открытием Декарта считают объединения им алгебры и геометрии, когда он точки на прямой и плоскости стал характеризовать числами (их координатами).
Но сама идея соединения чисел и фигур возбуждает ум ребенка и в самых простейших случаях. Мы приглашаем читателя совершить с детьми небольшое путешествие в мир чисел и фигур. Для этого нужно немногое: иметь под рукой клетчатую тетрадь и карандаш, разве еще уметь складывать в уме хотя бы в пределах 50!
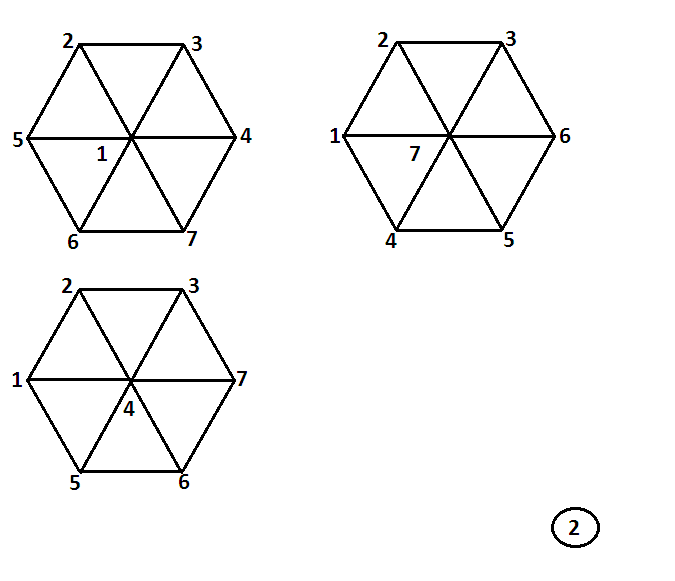
Пусть даны семь чисел: 1, 2, 3, 4, 5, 6, 7.
Требуется расположить их в вершинах шестиугольника и его центре так, чтобы суммы трех чисел на каждом диаметре были равны.
При каждом решении эта сумма наибольшая? Ответ можно увидеть (рисунок 2), сравнивая три решения (других нет).
Наиболее древней математической задачей, поражавшей воображение людей необъяснимой тайной сочетания постоянства и симметрии, были, несомненно, так называемые магические квадраты.
Магический квадрат третьего порядка (то есть три на три) был известен в Азии несколько тысяч лет назад; его считали талисманом, и по сей день там можно увидеть его изображение на амулетах.
Магический квадрат третьего порядка имеет постоянную сумму по любому из трех направлений, равную 15 (рисунок 3). 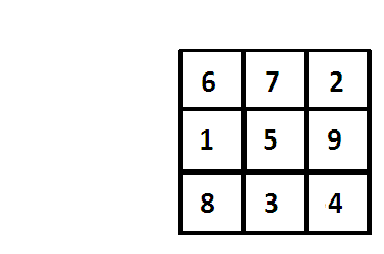

РР
Рассмотрите внимательно этот простейший магический квадрат и, закрыв его, попробуйте восстановить по памяти.
Интеллектуальное удовольствие, извлекаемое при постижении тайны составления магических квадратов, несравнимо с простым запоминанием готового расположения чисел – такое запоминание, впрочем, бывает обычно и непрочным.
Начнем с простого вопроса: почему постоянная сумма чисел квадрата третьего порядка должна равняться 15?
Найдем сумму чисел от 1 до 9, эта сумма равна 45. Как ни располагай числа в клетках квадрата, сумма их, понятно, меняться не будет. При специальном (магическом) расположении эта сумма должна распределиться поровну между тремя рядами; значит, сумма трех чисел в любом ряде будет равна 45:3=15.
Заполним каждую клетку квадрата третьего порядка пятеркой (рисунок 4).
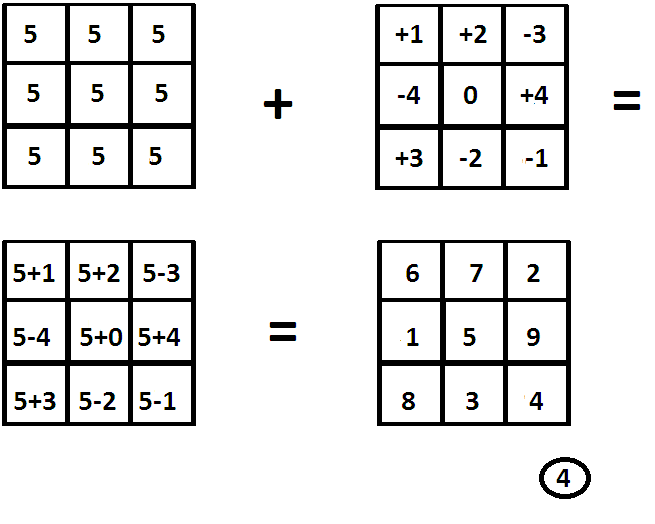
Составим в помощь себе квадрат с нулевой магической суммой по любому направлению. Этот квадрат легко запоминается, так как в нем симметричные числа противоположны, сумма чисел в каждом ряду равна нулю.
Сложив соответствующие элементы двух вспомогательных квадратов, получим искомый магический квадрат.
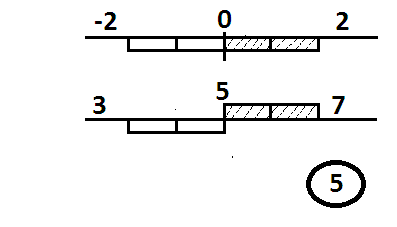
Заметим впрок следующее (это нам потом пригодится для построения магического куба третьего порядка). В центре квадрата число 5 – среднее число девятки. 1, 2, 3, 4, 5, 6, 7, 8, 9.
Подобно тому, как числа +2 и -2 на числовой оси симметричны относительно нуля, так и числа 7 и 3 симметричны относительно числа 5, так как они расположены правее и левее его на одном и том же расстоянии от среднего числа (рисунок 5). Мы видим, что магия чисел связана с пространственной симметрией.
Но вернемся к нашим квадратам.
Квадрат три на три – частный случай магических квадратов нечетного порядка; за ним следуют магические квадраты пять на пять, семь на семь и т.д.
Чтобы построить магический квадрат пятого порядка, рассуждаем так: в квадрате три на три среднее число 5, а в квадрате пять на пять средне число 13; 13 больше 5 на 8. Составим для квадрата пять на пять центральный квадрат три на три, для чего ко всем его числам прибавим по 8 (рисунок 6).
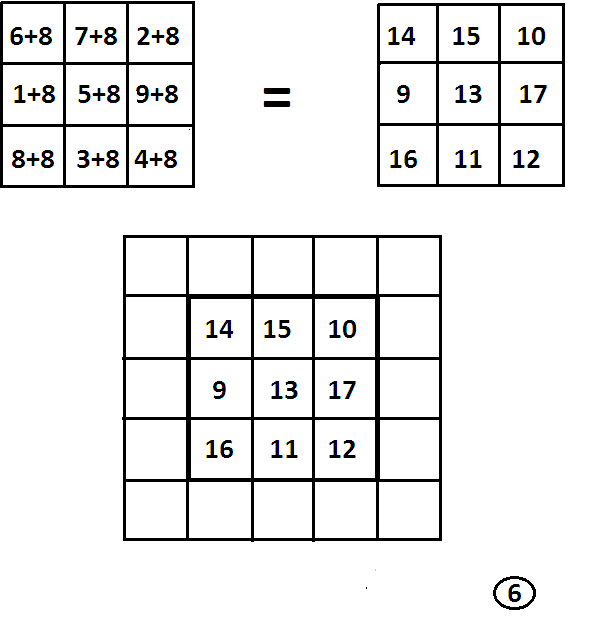
Предлагаем читателю закончить построение магического квадрата пять на пять, распределив оставшиеся числа (от 1 до 8 и от 18 до 25) клетках, окружающих квадрат три на три. ( Постоянную сумму магического квадрата пять на пять можно найти так же, как это мы делали раньше для квадрата три на три; она равна 65.)
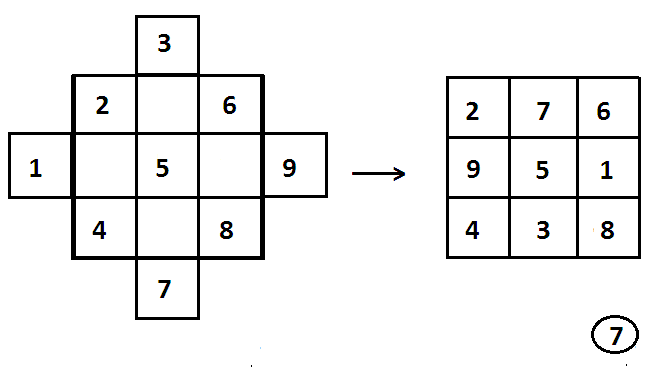
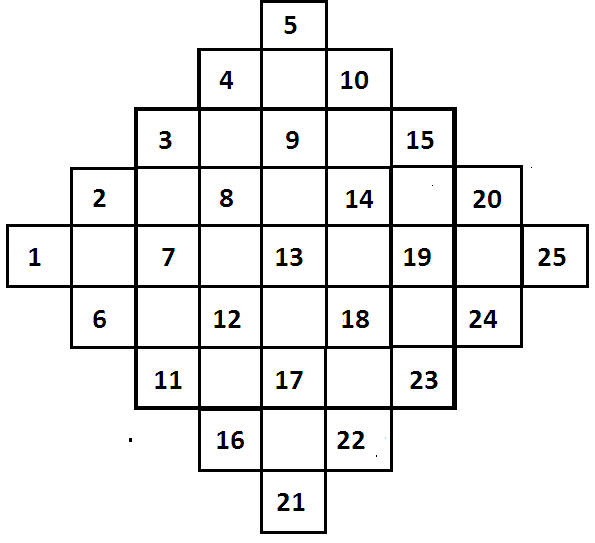
Удобен для обобщения другой метод (алгоритм) составления магических квадратов нечетного порядка, когда начинают с диагональной записи групп чисел. Из рисунка 7 видно, как строится (с помощью симметрического переноса чисел относительно осей симметрии) магический квадрат три на три. Дана также исходная запись для квадрата пять на пять; построение выполните сами.
Несколько труднее запомнить способ составления магического квадрата четвертого порядка (постоянная сумма 34). Квадрат четыре на четыре обладает совершенно удивительными свойствами (рисунок 8).
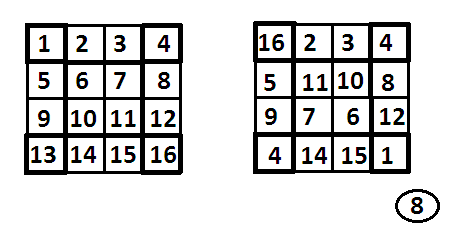
Сначала распишем числа от 1 до 16 последовательно в четырех рядах друг под другом.
Поменяем местами числа в противоположных вершинах (1 и 16, 4 и 13); так же сделаем с числами среднего квадрата (6 и 11, 7 и 10).
Оставив остальные числа на месте, получим искомый магический квадрат четвертого порядка.
Не зная этого приема, пришлось бы долго искать случайной удачи при методе случайной подгонки чисел в составляемом магическом квадрате.
Впрочем, можно разжечь огонь любопытства, у юного слушателя предложив ему самостоятельно найти какой-либо иной способ составления магического квадрата (существует много различных вариантов решения этой задачи).
Выделим в составленном нами квадрате какую-либо четверку чисел, образующих квадрат два на два; так, четверка чисел 9, 7, 4, 14 в левом нижнем углу обладает тем замечательным свойством, что в сумме они составляют опять-таки 34 (рисунок 9).
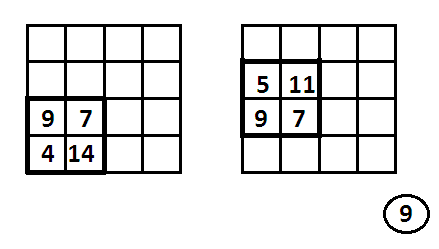
Но получается ли тоже самое в нашем квадрате для любой подобной четверке? Нетрудно убедиться, что для некоторых групп четверок это не так, например, для чисел 5, 11 9, 7.
Можно ли составить такой квадрат, чтобы в нем любая такая группа четверок в сумме составляла 34? Математики нашли такой квадрат. Вы видите его на рисунке 10.
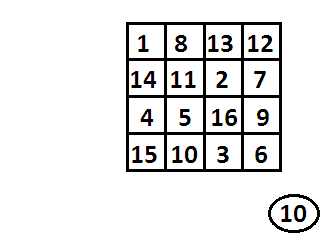
Этот квадрат был назван «дьявольским». Мало того, что сумма 34 образует четверки чисел по всем направлениям (как во всяком магическом квадрате). Мало того, что такую сумму дает любой квадрат два на два, выбранный внутри него. Оказывается, есть еще десять конфигураций, видов взаиморасположения четырех клеток квадрата, в которых выполняется то же условие! Но об этом мы поговорим в следующий раз. (А вы со своим ребенком-школьником, быть может, найдете пока некоторые из этих конфигураций? )









































