РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ СРЕДСТВАМИ ПРЕДМЕТНЫХ И ГРАФИЧЕСКИХ МОДЕЛЕЙ НА УРОКАХ МАТЕМАТИКИ 1 КЛАССА
С.В. Мацуева
студентка
Красноярский педагогический колледж им. Горького
Научный руководитель преподаватель математики Т.А. Вахромеева
КГБПОУ «Красноярский педагогический колледж №1 им. М. Горького»
Аннотация. В основе Федерального государственного образовательного стандарта начального общего образования заложена концепция формирования универсальных учебных действий. Логические действия относятся к одному из видов универсальных учебных действий. Их формирование является важной составляющей работы учителей начальных классов, так как логические операции способствуют развитию у младших школьников активной познавательной позиции. В начальной школе наибольшую возможность для формирования логических действий имеет предмет математика. По мнению различных авторов, предметные и графические модели способствуют научить учащегося решать логические задачи. В статье подробно раскрывается, как решать логические задачи с помощью предметных и графических моделей на уроках математики 1 класса.
Ключевые слова: предметная модель, графическая модель, логическое мышление
На уровне начального общего образования изучение математики имеет особое значение в развитии обучающего. Приобретённые им знания, опыт выполнения предметных и универсальных действий станут фундаментом обучения в дальнейшем.
В федеральном государственной образовательной стандарте начального общего образования в пункте №42.1 разделе №3 «работа с информацией» говорится о том, что обучающимся нужно «анализировать и создавать текстовую, видео, графическую, звуковую, информацию в соответствии с учебной задачей». [3.18] В предметных результатах по учебному предмету «Математика» рассматривается развитие логического мышления – это «умения распознавать верные (истинные) и неверные (ложные) утверждения в простейших случаях в учебных и практических ситуациях, приводить пример и контрпример, строить простейшие алгоритмы и использовать изученные алгоритмы (вычислений, измерений) в учебных ситуациях» [3.25]
Таким образом, мы видим, что развитие логического мышления является в приоритете и для этого используются графические модели.
Формирование логического мышления у детей младшего школьного возраста, по мнению Вергелес Г.И., - одна из основных задач обучения в начальном курсе математики. [2]
Многочисленные наблюдения педагогов, таких, как например Зака А. З. показали, что ребёнок, не научившийся учиться, не овладевший базовыми приёмами мыслительной деятельности, обычно переходит в разряд неуспевающих. С 1 класса необходимо учить анализировать, рассуждать, делать выводы.
Э.И. Александрова считает, что предметную модель в 1 классе можно использовать для сравнения объектов по различным признакам (по цвету, по форме, по размеру). [1]
Для использования графической модели, по мнению Э.И. Александровой, необходимо задать конкретно-практическую задачу. [1]
Применение предметных и графических моделей для формирования логического мышления позволяет наглядно показать решение логической задачи.
Решение логических задач с помощью предметной модели
Предметная модель – физическое действие с предметами: палочки, пуговицы, полоски бумаги и т.п. К этому виду моделей относятся и мысленное воссоздание реальной ситуации, описанной в задаче. (К.А. Малюгина)
Уже с 1 класса на уроке математика учащимся нужно давать возможность решать логические задачи. Здесь мы рассмотрим задачи, которые решаются с помощью предметной модели.
Пример1: Маша выше Пети, Петя выше Коли. Кто самый высокий?
В качестве предметной модели учащимся можно предложить полоски из бумаги. Берём полоску нужной нам длины и подписываем соответствующими именами, опираясь на условие задачи.

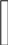

Маша Петя Коля
Здесь мы видим, полоска с именем Маша самая высокая. Исходя из условия задачи следует, что самой высокой является Маша.
Такой метод можно использовать с задачами, которые имеют формулировки «больше», «меньше», «выше», «ниже» и т.д. Также, в качестве предметной модели можно использовать реальные объекты и предметы.
Пример2: Если красное яблоко больше жёлтого, а жёлтое больше зелёного, то какое меньше всех?
В качестве предметной модели учащиеся могут использовать сами яблоки или вырезанные из бумаги круги соответствующего цвета.



Представив предметную модель в таком виде, можно сделать вывод о том, что зелёное яблоко меньше всех. Предметная модель позволяет наглядно увидеть условие задачи и решить её, те самым, развивая логическое мышление. По такому же принципу решаются и остальные задачи. Главное, дать установку учащимся на использование предметных моделей и показать наглядный пример. Использование предметных моделей поможет учащимся 1 класса научиться решать простые логические задачи и развить логическое мышление.
Примеры задач на логическое мышление с использованием предметной модели
Если бы лошадь была ниже кролика и больше жирафа, то кто был бы выше всех?
Летели утки: одна впереди и две позади, одна и две впереди. Одна между двух и три в ряд. Сколько всего летело уток?
Дуб выше Берёзы, Берёза выше Рябины. Какое дерево выше всех?
Ваня старше Вовы, а Вова старше Кости. Кто из мальчиков младше всех?
Сколько ушей у трёх мышей?
Решение логических задач с помощью графической модели
Графическая модель – изображение, реализованное с помощью графического действия, которое не только воспроизводит объект исследования, его отдельные свойства и отношения, но и позволяет осуществить их дальнейшее изучение. ( Н.В. Нашалахова)
В учебниках 1-го класса по математике можно встретить задачи, где используется графическая модель. К 1 классе в качестве графической модели используются схемы, таблицы.
Пример1: В стакан, банку и кувшин налили молоко, квас, компот. В стакане не компот, в кувшине не квас и не компот. Где что налито?
В данной задаче уместно использовать в качестве графической модели таблицу. В таблице нужно обозначить все объекты, которые показаны в условии задачи.
| Название объекта | Стакан | Банка | Кувшин |
| Молоко | - | - | + |
| Квас | + | - | - |
| Компот | - | + | - |
Данная задача требует подробного и логического рассуждения. Для начала, нужно начертить таблицу и знаком «-» отметить варианты, которые не рассматриваются, исходя из условия задачи. Так, например, в задаче сказано, что в стакане нет компота, значит в колонке мы ставим «-», этот вариант сразу не рассматривается. Исходя из условия задачи, в кувшине не налит квас и компот. Уместно предположить, что в кувшине находится молоко. Поэтому, в колонке на этом месте ставим «+». Проведя подобные логические рассуждения, можно сделать вывод о том, что в стакане квас, в банке компот, в кувшине молоко.
В данной задаче с помощью графической модели в виде таблицы мы провели цепочку логических рассуждений, которые позволили сделать нам правильный вывод к задаче. В таком случае, графическая модель в виде таблицы позволяет развивать умение проводить логические рассуждения.
Пример 2: Гепард пробежал дальше, чем тигр. Кто пробежал меньше?
В данной задаче уместно создать схему, которая позволит наглядно увидеть ответ к задаче.
Г епард
епард
Т игр
игр
Исходя из данных в графической модели в виде схемы мы видим, что тигр пробежал меньше всего. Такого рода логические задачи позволяют обучающимся 1-го класса наглядно и с ходу сказать правильный ответ.
Примеры логических задач с использованием графических моделей
1. В трёх тарелках лежат разные фрукты. Бананы лежат не в синей и не в оранжевой тарелке. Апельсины не в синей и не в розовой тарелке. В какой тарелке лежат сливы? А бананы и апельсины?
2. Под ёлкой цветок не растёт, под берёзой не растёт не грибок. Что растёт под ёлкой? Что растёт под берёзой?
3. Самолёт движется быстрее, чем поезд. Кто приедет позже?
4. По дорожке из жёлтого кирпича идут: Элли, Тотошка, Лев, Страшила и Железный Дровосек. Элли идет впереди Железного Дровосека, Страшила впереди Тотошки, Железный Дровосек впереди Страшилы, а Тотошка обогнал Льва. В каком порядке идут сказочные герои?
5. Дерево распилили на 5 частей. Сколько раз подряд распилили дерево?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Александрова, Э.И. Методика обучения математике в начальной школе. 1 класс: Пособие для учителя.— электрон. текст;
Особенности развития логического мышления младших школьников // З.М. Бобоева, 2022;
Федеральный государственный образовательный стандарт начального общего образования (Утвержден приказом Министерства образования и науки Российской Федерации от 31.05.2021 № 286) — М.: Просвещение, 2021 — 18 с;












 епард
епард игр
игр 









