уравнения и неравенства как математические модели
Содержание
| Введение………………………………………………………………… | 3 |
| 1.Примеры решения уравнений с параметрами как математической модели……………………………………………………………………….. |
4 |
| 1.1.Вид соотношений с выделенными параметрами…………………… | 5 |
| 1.2. Пример решения неравенства с параметром……………………. | 6 |
| Заключение………………………………………………………………… | 10 |
| Список литературы………………………………………………………. | 11 |
Введение
Математическая статистика − наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Любой творчески работающий специалист физического воспитания в ходе своей работы получают фактический экспериментальный материал (первичный цифровой массив). Если эти данные не будут корректно обработаны с помощью методов математической статистики, то их работа теряет всякий теоретический и практический смысл.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
Цель: проанализировать уравнения и неравенства как математические модели.
Задачи:
Провести теоретический анализ литературы по теме исследования.
Рассмотреть:
примеры решения уравнений с параметрами как математической модели;
вид соотношений с выделенными параметрами;
пример решения неравенства с параметром.
Сформулировать выводы.
1.Примеры решения уравнений с параметрами как математической модели
Ряд проблем в различных отраслях человеческой деятельности может быть изучен математическими методами. На этом пути, применяя язык математики, изучаемым явлениям ставят в соответствие модельные явления. Если они описаны с помощью математических правил, то такие модели называются математическими. Примером такого процесса является процесс решения простейших так называемых «текстовых» задач с помощью сведения их к уравнениям или неравенствам [7].
Любая предметная область характеризуется своим набором понятий связей между ними. Каждая предметная область имеет свои специфические методы решения задач. Необходимость в формализованном представлении знаний возникла в связи с их обработкой средствами компьютерной техники. Методология моделирования и формализации концептуальных знаний, ориентированная на их компьютерную обработку, является одной из основных тем развития искусственного интеллекта [7].
Под моделью мы будем понимать «систему произвольной природы, отражающую свойства, характеристики и связи моделируемого объекта (объекта-оригинала), которые считаются существенными для решения данной задачи» [5, с. 46]. При этом отсутствие в модели несущественных элементов не менее важно, чем присутствие в ней существенных.
Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала. Полное соответствие модели оригиналу невозможно по определению.
Приведем пример.
Пример. Рассмотрим уравнение 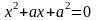 . Его можно понимать как квадратное уравнение относительно неизвестного х , а можно понимать как квадратное уравнение относительно неизвестного а с параметром х. Следует же понимать это уравнение как уравнение с двумя неизвестными х и а. В левой части уравнения стоит математическое выражение от двух аргументов х и а.
. Его можно понимать как квадратное уравнение относительно неизвестного х , а можно понимать как квадратное уравнение относительно неизвестного а с параметром х. Следует же понимать это уравнение как уравнение с двумя неизвестными х и а. В левой части уравнения стоит математическое выражение от двух аргументов х и а.
Множество решений такого уравнения – это множество пар чисел, при подстановке которых в уравнение получается верное равенство.
Взгляд относительно х говорит о решении уравнения относительно х. В этом случае аргументы х и а считают неравноправными. Поэтому необходимо выразить при решении х через а, которое называют «параметром».
Можно рассмотреть это уравнение по-другому, взгляд относительно а: необходимо иметь ответ в таком виде, чтобы для каждого значения а было указано, какие числа х в паре с этом а дают решения данного уравнения.
На этом пути, если брать разные основания для классификаций (например, от вида математического выражения, задающего уравнение) и учитывая разные взгляды на аргументы, входящие в это математическое выражение, получим спектр разных типов уравнений (неравенств).
1.1.Вид соотношений с выделенными параметрами
В реальных задачах (например, с физическим содержанием) естественно вводится неравноправие аргументов, входящих в уравнение. Они делятся на «неизвестные», обозначаемые, как правило, последними буквами латинского алфавита (…, x, y, z), и «параметры» – обозначаемые первыми буквами (a, b, c,…) [7].
Рассмотрим один из способов решения задачи с параметрами:
значение параметра (или параметров, если их несколько) считается произвольно фиксированным, и затем ищется решение задачи так, как обычно обращаются с уравнениями и неравенствами с одним неизвестным.
Ответом должно быть перечисление решений для каждого допустимого значения параметра.
Например, ответ при решении неравенства 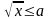 лучше всего записывать в виде:
лучше всего записывать в виде:
при 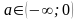 решений нет;
решений нет;
при 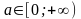 имеем любое х из
имеем любое х из 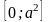 [7].
[7].
Отметим, что выяснение зависимости решений от значений параметра есть часть процесса решения задачи. Иногда это называют исследованием и отделяют от непосредственного решения. Необходимо запомнить и уяснить, что решение задачи с параметрами без такого этапа не дает решение. Задача нерешена!
1.2.Пример решения неравенства с параметром
Решить неравенство
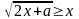 .
.
Решение. 1) Находим естественную область определения. Это множество пар 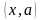 , при которых выражение, задающее задачу определено. Имеем, что
, при которых выражение, задающее задачу определено. Имеем, что 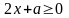

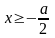 .
.
2) Так как 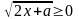 рассмотрим сначала случай
рассмотрим сначала случай 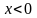 . Тогда все пары
. Тогда все пары 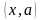 , входящие в область определения, являются решениями.
, входящие в область определения, являются решениями.
3) Рассмотрим случай 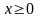 . Тогда
. Тогда 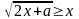

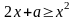

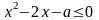 . Исследуем дискриминант получившегося трехчлена. Он равен
. Исследуем дискриминант получившегося трехчлена. Он равен 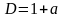 .
.
3.1. При 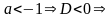 действительных решений нет.
действительных решений нет.
3.2. При 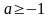 , решая квадратное неравенство, имеем, что
, решая квадратное неравенство, имеем, что 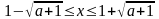 . Однако теперь надо согласовать полученное условие с условиями:
. Однако теперь надо согласовать полученное условие с условиями: 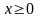 и
и 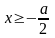 . Это при водит к системе неравенств: Получаем, что х должен быть больше (или равен) каждого из трёх чисел 0,
. Это при водит к системе неравенств: Получаем, что х должен быть больше (или равен) каждого из трёх чисел 0, 
 . Поэтому надо знать, как они расположены на числовой оси в зависимости от параметра а. Рассмотрим варианты: а) первое число больше третьего .
. Поэтому надо знать, как они расположены на числовой оси в зависимости от параметра а. Рассмотрим варианты: а) первое число больше третьего .
б) первое число больше второго  .
.
Получаем два случая:  и
и  .
.
3.2.1) Пусть  . В этом случае из трех исходных чисел самым большим является первое – число 0. Остаются условия
. В этом случае из трех исходных чисел самым большим является первое – число 0. Остаются условия 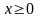 и
и  .
.
3.2.2) Пусть  . Теперь первое число меньше второго и третьего. Сравним второе и третье:
. Теперь первое число меньше второго и третьего. Сравним второе и третье: 


 .
.
Это не выполняется ни при каких а. Итак, в этом случае третье число наибольшее. Получили, что 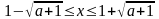 . Объединив все случаи, получим
. Объединив все случаи, получим
Ответ. 1) если  , то решений нет;
, то решений нет;
2) если  , то
, то 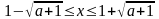 ;
;
3) если  , то
, то  .
.
Как уже отмечалось, задачи с параметрами могут бать по-разному классифицированы:
по виду математического выражения (линейные, квадратные и т.д.);
по количеству неизвестных и выражений (системы и т.д.);
по количеству параметров [7].
Выделены и классы методов их решения (формальный, геометрический и др.).
Пример математической модели.
Задача
Производственное объединение, в которое входят две мебельные фабрики, нуждается в обновлении парка станков. Причем первой мебельной фабрике нужно заменить три станка, а второй-семь. Заказы можно разместить на двух станкостроительных заводах. Первый завод может изготовить не более 6 станков, а второй завод примет заказ если их будет не мение трех. Требуется определить как размещать заказы [8].
Решение
Введем переменные: xij-количество станков, которое будет изготавливать i-й завод для j-й фабрики.
По условию задачи:
x11+x12 6
6
x21+x22 3
3
Кроме того, должны выполняться условия:
x11+x21=3
x12+x22=7
Получаем систему ограничений в форме неравенств и уравнений:
x11+x21=3
x12+x22=7
x11+x12 6
6
x21+x22 3
3
xij 0; i=1,2; j=1,2;
0; i=1,2; j=1,2;
Мы составили математическую модель нашей задачи. Решая систему мы найдем множество различных решений. Вот одно из них:
x11 = 2,
x12 = 3,
x21 = 1,
x22 = 4.
Оптимальное решение будет зависеть от других параметров, отдаленности заводов, цены на станки и т.д.
Заключение
Таким образом, в ходе исследования мы проанализировали уравнения и неравенства как математические модели.
Рассмотрели:
примеры решения уравнений с параметрами как математической модели;
вид соотношений с выделенными параметрами;
пример решения неравенства с параметром.
Список литературы
Бантова М.А. Методическое пособие к учебнику математики. – М.: Просвещение, 2011. – 64 с.
Гусева, Е.Н. Экономико-математическое моделирование. – М.: Флинта, 2011. – 439 с.
Лагутин, М.Б. Наглядная математическая статистика. – М.: Бином. Лаборатория знаний, 2011. – 472 с.
Трусов, П. Введение в математическое моделирование. – М.: Логос, 2009. – 440 с.
Чикаш, С.Л. Математическая статистика в спорте. − Улан-Удэ: Издательство Бурятского госуниверситета, 2007. − 58 с.
Шеломовский, В.В. Математическая статистика. – Мурманск: МГПУ, 2009. – 128 с.
Уравнения и неравенства с параметрами как математические модели [Текст]: http://school-collection.iv-edu.ru/dlrstore/5d6a86b6-66ed-5934-b848-6708d909049d/11_13.doc
Математическое моделирование [Текст]: http://www.wikiznanie.ru/ru-wz/index.php/Математическое_моделирование





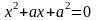 . Его можно понимать как квадратное уравнение относительно неизвестного х , а можно понимать как квадратное уравнение относительно неизвестного а с параметром х. Следует же понимать это уравнение как уравнение с двумя неизвестными х и а. В левой части уравнения стоит математическое выражение от двух аргументов х и а.
. Его можно понимать как квадратное уравнение относительно неизвестного х , а можно понимать как квадратное уравнение относительно неизвестного а с параметром х. Следует же понимать это уравнение как уравнение с двумя неизвестными х и а. В левой части уравнения стоит математическое выражение от двух аргументов х и а.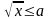 лучше всего записывать в виде:
лучше всего записывать в виде: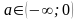 решений нет;
решений нет;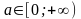 имеем любое х из
имеем любое х из 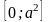 [7].
[7].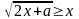 .
.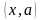 , при которых выражение, задающее задачу определено. Имеем, что
, при которых выражение, задающее задачу определено. Имеем, что 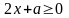

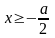 .
.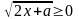 рассмотрим сначала случай
рассмотрим сначала случай 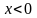 . Тогда все пары
. Тогда все пары 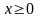 . Тогда
. Тогда 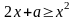
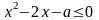 . Исследуем дискриминант получившегося трехчлена. Он равен
. Исследуем дискриминант получившегося трехчлена. Он равен 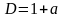 .
.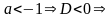 действительных решений нет.
действительных решений нет.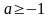 , решая квадратное неравенство, имеем, что
, решая квадратное неравенство, имеем, что 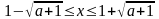 . Однако теперь надо согласовать полученное условие с условиями:
. Однако теперь надо согласовать полученное условие с условиями: 









