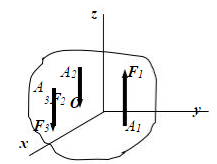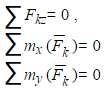Статика. Устойчивость равновесия

Условия равновесия системы параллельных сил

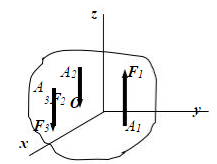
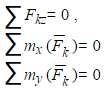
1. 16 Условия равновесия тел при его опрокидывании

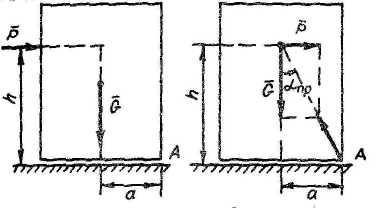
Силы, прилож к свободностоящ телу, м привести к его опрокид как получить усл неопро­кид тела, рассм прямоуг параллелеп (весом G), свободно стоящий на гориз шерохо плти (коэф трения f). Найдем усл неопрокид параллелепип под дейст­вием силы р (см. Рис).В пред полож равновесия тела (положе, предш его опрокид, когда реакция шерохов поверхности прил в т. A)

; ; .

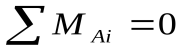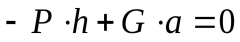Тогда условия неопроки­дывания примут вид:

а) по величине силы; б) по величине плеча ;

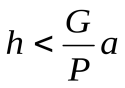в) по углу, составл равнодействующей сил P и G с вертикалью

;г) в общем случае произвольной системы сил,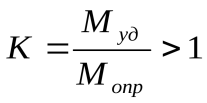

M_уд - удержив момент;M_опр - опрокидыв момент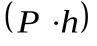;K - коэфф устойчивости.

Пр1 Проверка устойчивости кра­на, если вес поднимаемого груза G_г, вес крана G_к, вес противо-веса G_п, ветр нагрузка P_в. Коэффициент устойчивости д б не менее k = 1,25. Груз подним равно. На рис раз­меры - в метрах. G_г = 50 кН; G_к = 600 кН; G_п = 25 кН; P_в = 12 кН.

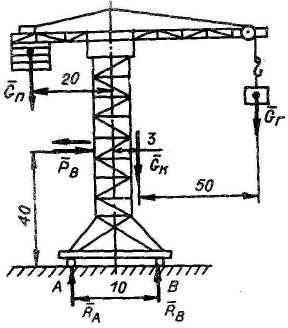
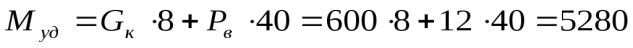
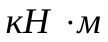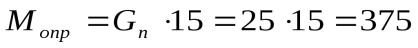
1. Кран без груза Опрокидывание возм вокруг т. A. В положении предельного равновесия реакция R_в = 0. Направление ветра вправо:; ;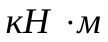k = 14,0 - кран устойчив.

Направление ветра влево:

 ;;

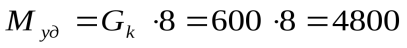
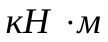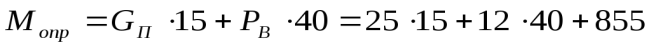
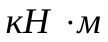2. Кран с грузом

Опрокидывание возможно вокруг т B. В положении предельного равновесия реакции R_A = 0. Направл вет­ра вправо:

 ;

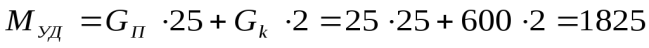
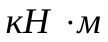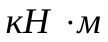; k = 0,63 - кран неустойчив.

Вывод: при ветре кран к эксплуатации непригоден.

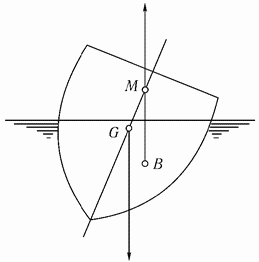
Если ц т выше метацентра, то равновесие неустойчиво, а результир момент от откл стремится увел угол наклона до тех пор, пока корабль не опрокинется.

Система 2 параллельных сил на ломаном рычаге (опрокидывание прямоугольника)

Заменим силы P, Q эквивал равнодействующей P+Q делящей концы рычага в от сводим задачу к эквивал физическому маятнику . Сл А)-качания большой амплитуды –неустойчивое равновесие. Сл б) –качания небольшой ампл справа – большая амплитуда – полное опрокидывание

Статическое равновесие — это такое равновесие когда под действием приложений сил тело находится в состоянии покоя.

Динамическое равновесие — это такое равновесие, когда под действием сил тело не изменяет своего движения

положение равновесия системы q₁ = q₂ = ...= q_s  = 0 назыв устойчивым, если всегда м найти такие дост малые начальные знач , при кот  движение системы  не б выходить из любой зад сколь угодно малой окрестн положения равновесия . Для с-мы с 1 ст свободы устойч движение системы м наглядно изобр в фазовой пло=ти (рис. Для устойч положения равновесия движение изобр точки, нач в обл [], не будет в дальн выходить за пределы обл .

Если механич с-ма нах в равновесии в потенц силовом поле, то получ след усл равновесия:

Т Лагранжа - Дирихле: положение равновесия консервативной механич системы устойчиво, если в полож равновесия потенциальная энергия системы имеет изолированный минимум

т1 Кельвина: Наличие диссипат сил не нарушает устойч полож равновесия (система б перемещаться до тех пор пока не уравновесится).

т2 Кельвина: Добавление диссипативных сил увеличивает устойчивость положения равновесия.

т3 Кельвина: Никакими диссипат силами нельзя превратить неустойч положение в устойчивое.

Т2 Томпсона-Кэта. Если состояние равновесия консервативной с-мы устойчиво то при добав-лении диссипативных и гироскопических сил устойчивость сохраняется.

Критерий Сильвестра

Выражение для потениальной энергии системы в обобщенных координатах

1 степень свободы	S степеней свободы
	-обобщенные к-ты жесткости

чтобы квадратичная форма с вещ коэфф б опред-положит, необх и дост, чтоб все гл диаг миноры А _1г Д₂, . . ., А_п матрицы ее коэфф б положит, т. е.

Разложим эту ф в ряд по степ х_х и х₂. Имеем

усл Сильвестра вып (все ) и поэтому ф V в окр пуля определ положит. на всей пл=ти х_гх₂ ф V только положительна,

Проверка устойчивости равновесия физического маятника с несколькими пружинами

Пусть есть тело с неподвижной осью вращения (физический маятник) закрепленное в к точках пружинами.

-жесткость i-пружины, координаты точки закрепления в теле

координаты точки закрепления (опоры) 2 конца пружины

- длина i-пружины в нерастянутом состоянии

Предполагаем пружины достаточно длинными, их деформация при повороте маятника – в рамках закона Гука.

Выражение для потенциальной энергии системы в зависимости от угла поворота имеет вид

Переменная составляющая (зависимость от угла поворота )имеет вид

Периодическая функция лостигает хотя бы одного минимума и максимума.Значит есть по меньшей мере 1 устойчивое и неустойчивое положение равновесия

Пр1 Равновесие маятника с пружиной

Если то вып усл Лагранжа–Дирихле - устойчивое положение равновесия.

Если т о положение неустойчиво– согласно т 2 Ляпунова

При явл устойчивым реш – по т Лагранжа–Дирихле.

При устойчиво

Пр2 Маятник с 2 пружинами жесткости с натянутыми силами

Проверка устойчивости равновесия

Примем угол отклонения маятника влево малым ..Рассматриваем линеаризованные уравнения. Полагаем Из теоремы синусов (рис ниже)

Обозначим тогда

Длины пружин

левая пружина укоротится на а правая удлинится на Новые значения сил упругости пружин = =

их проекции на тангенциальное направление

момент - будет отрицательным (устойчивое равновесие) при выполнении условия

определение положений устойчивого равновесия через минимум потенциальной энергии

для прим.2 воспользуемся (1) подставив в нее значения координат, длин, жесткостей

=0,=0 тогда

=

Условие экстремума

2 решения

а) б)

Легко убедиться, что функция достигает максимума

при , т.е неустойчивые положения равновесия

и минимума при т е. устойчивые положения равновесия

Пр3 Физический маятник соединенный с грузом через шкив

Условие равновесия

Условие равновесия

потенц энергия не имеет мин при

Нет устойчивого равновесия

53.5 На гладкий цилиндр радиуса r опираются 2 однородных тяжелых стержня, соед шарниром A. Длина каждого стержня 2a. Опр угол 2ϑ раствора стержней, соотв положению равновесия

Пр2 определения положений равновесия и исследования их устойчивости

Рис.2

Рассм механич систему, из трубки AB, кот стержнем OO₁ соед с гориз осью вращ, и шарика, кот перемещ по трубке без трения  и связан с то A трубки пружиной рис. Опр полож равнов симы и оценим их устойч при след парам: длина трубки l₂= 1 м, длина стержня  l₁ =0,5 м.  длина недеформир пружины l₀ = 0,6 м , жестк пружины c = 100 Н/м. Масса трубки  m₂ = 2 кг , стержня - m₁ = 1 кг и шарика - m₃ = 0,5 кг. Расст OA равно l₃   =  0,4 м.

потенц энергии с-мы склад из потен энергии 3 тел, нах в однородном поле силы тяжести, и потенц энергии деформир пружины. Потенц эн тела в поле силы тяжести= произв веса тела на высоту его ц т над пл\тью, в кот потенци энергия счит=0. Пусть потенц энергия=0 в плоскости, проходящей через ось вращения стержня OO₁ , тогда для сил тяжести

Для силы упругости потенциальная энергия опр вел деформации 

Найдем возможные положения равновесия системы. Значения координат в положении равнове-сия есть корни следующей системы уравнений.

Подоб сму ур м составить для любой мех системы с 2 ст сво. В некот сл м получить точное реш системы. Для смы (5) такого реш не сущест, поэтому корни н искать с пом численных методов.

Решая систему трансценд уравн (5), получаем два возм положения равновесия:

Для оценки устойч получ полож равнове найдем все 2е производ от потенц энергии по обобщ координатам и по ним определим обоб коэффициенты жесткости.

Тогда для 1 полож равнов

Восп критерием Сильвестра

Для 2го полож равнов

Таким обр, 1е положение равновесия устойчиво, 2е - неустойчиво.

M53.14 Иссл устойчивость вертикального положения равновесия «обращенного двойного маятника, на рис. Маятник м б схематизнр в виде 2 мат точек масс m₁ и m₂, связ стержнями длин l₁ и l₂. В вертикальном полож равновесия пружины (жесткости их k₁ и k₂) не напряжены. M53.16 В маятнике паллографа груз M подвеш на стержне OM, свободно прох через вращ цилиндрик O и шарнирно соед в т A с коромыслом AO₁, вращ около оси O₁. Длина коромысла r, расст от ц ма груза до шарнира A l, расст OO₁=h. Исследовать устойчивое вертикальное поло-жение равновесия маятника. Размером груза и массой стержней пренебречь.

Для консервативных сил выполняются следующие тождества:

 — ротор консервативных сил равен 0; — работа консервативных сил по произв замкнутому контуру =0;  — консервативная сила явл градиентом некой скалярной функции , называемой силовой.

Устойчивость с-мы электрических зарядов

Т Ирншоу Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кр кулоновских сил притяжения и отталкивания не действует иные силы. для сил ньютоновской гравитации  у системы из любого числа зарядов при любом их расположении  потенциальная  энергия взаимодействия не имеет минимума и потому устойчивое статическое распределение  электрических зарядов, находящихся на конечном расстоянии др от др невозможно.

из нее б сделан вывод о том, что атом не предст статич (неподв) систему зарядов и что устойч атома м б обесп только непрер движением его частиц — электронов

Томсоновская модель атома	Модель атома Резерфорда — Бора.
1 — однородно распред положи­т заряд; 2 — отриц заряд, сконц в центре Раз заряды не могут иметь устойч полож, то,, непр предст вещество постр из статич точечных зарядов (эл-нов и протонов), управл только з нами электростатики.	1 — положительные ядра в центре; 2 — отрицательные электроны на планетных орбитах.

.

http://studopedya.ru/1-70321.html