Статистический анализ
итоговой аттестации выпускников
по математике
Исследовательская работа по «Статистике»
МБОУ Школа № 31 г. Ростова-на-Дону
Кряквина Л.Н.,
учитель математики
2007 год
Оглавление
стр.
1.Введение……………………………………………………… 3
2. Основная часть (результаты исследования)……………………… 4
3. Выводы по материалам исследования…………………………….. 9
4. Приложения………………………………………………………… 10
5. Список использованной литературы……………………………… 16
Введение
Целью работы является анализ результатов итоговой аттестации учащихся 11 классов по математике на основе методов математической статистики.
Математическая статистика возникла в 17 веке и развивалась параллельно с теорией вероятностей. Дальнейшее развитие математической статистики (вторая половина 19 – начало 20 века) обязано, в первую очередь П.Л.Чебышеву, А.А.Маркову, А.М.Ляпунову, а также К.Гауссу, А.Кетле, Ф.Гальтону, К.Пирсону и др. [3].
В 20 веке наиболее существенный вклад в математическую статистику был сделан российскими математиками (В.И.Романовский, Е.Е.Слуцкий, А.Н.Колмогоров, Н.В.Смирнов), а также английскими (Стьюдент, Р.Фишер, Э.Пирсон) и американскими (Ю.Нейман, А.Вальд) учеными.
Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности. Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Важнейшим показателем качества образования является объективная оценка учебных достижений учащихся. Этот показатель важен как для всей системы образования, так и для каждого отдельного ученика. Важной особенностью ЕГЭ является оценка уровня подготовленности учащихся с учетом уровня трудности и дифференцирующей силы верно выполненных заданий.
ЕГЭ по математике как эксперимент проводится по России с 2001 года. С 2002 года в этот эксперимент включены и школы Ростовской области.
Поэтому возникла необходимость определения корреляции (некоторой статистической зависимости) годовых оценок и результатов ЕГЭ.
Данная работа содержит основные определения и формулы, которые были использованы для расчетов.
В работе проведены исследования результатов ЕГЭ по математике выпускников МОУ СОШ № 31 с 2004 по 2006 год на основе методов математической статистики. На основе годовых оценок и оценок по ЕГЭ учащихся 11-х классов были вычислены выборочное среднее квадратичное отклонение и выборочный коэффициент корреляции, а также составлена эмпирическая функция по данному распределению выборки (на основе оценок, полученных на ЕГЭ за три года) и для наглядности построены полигоны и гистограммы частот распределения.
Результаты исследования.
Введем основные определения.
Эмпирическая функция распределения [1].
Пусть известно статистическое распределение частот количественного признака Х. Пусть nx – число наблюдений, при которых наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем выборки). Если х изменяется, то изменяется и относительная частота, т.е. относительная частота nx/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Хx/n, где nx – число вариант, меньших х , n - объем выборки.
Свойства функции F*(x):
значения эмпирической функции принадлежат отрезку [0;1];
F*(x) – неубывающая функция;
если х1 – наименьшая варианта, то F*(x)=0 при х1; если xk – наибольшая варианта, то F*(x)=1 при хxk.
Полигон и гистограмма [1].
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1;n1); (x2;n2);…(xk;nk). Для построения полигона частот на оси абсцисс откладываю варианты xi, а на оси ординат – соответствующие им частоты ni.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников. основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна hni/h=ni – сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Выборочная средняя [1],[2].
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.
Выборочной средней 
 n называют среднее арифметическое значение признака выборочной совокупности. Если все значения x1 , x2 ,…xk признака выборки объема n различны, то
n называют среднее арифметическое значение признака выборочной совокупности. Если все значения x1 , x2 ,…xk признака выборки объема n различны, то 
 n = (x1 + x2 +… + xn)/n.
n = (x1 + x2 +… + xn)/n.
Если же значения признака x1 , x2 ,…xk имеют соответственно частоты n1, n2, …nk, причем n1 + n2 +… + nk = n, то 
 n = (x1 n1 + x2 n2 +… + xk nk)/n (1).
n = (x1 n1 + x2 n2 +… + xk nk)/n (1).
Отклонение от общей средней.
Рассмотрим совокупность значений количественного признака Х объема n:
значения признака x1 , x2 ,…xk
частоты n1, n2, …nk
При этом n1 + n2 +… + nk = n. Обозначим эту сумму знаком 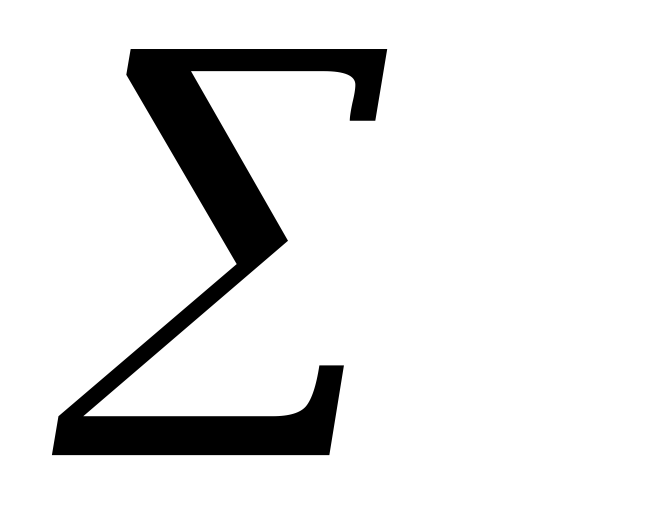 .
.
Найдем общую среднюю: 
 n = (
n = ( )/n.
)/n.
Отсюда  = n
= n . Заметим, что поскольку
. Заметим, что поскольку  - постоянная величина, то
- постоянная величина, то  .
.
Отклонением называют разность xi - 
 n между значением признака и общей средней.
n между значением признака и общей средней.
Выборочная дисперсия [1],[2].
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 
 n , вводят сводную характеристику – выборочную дисперсию.
n , вводят сводную характеристику – выборочную дисперсию.
Выборочной дисперсией Dn называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 
 n.
n.
Если все значения x1 , x2 ,…xk признака выборки объема n различны, то Dn=(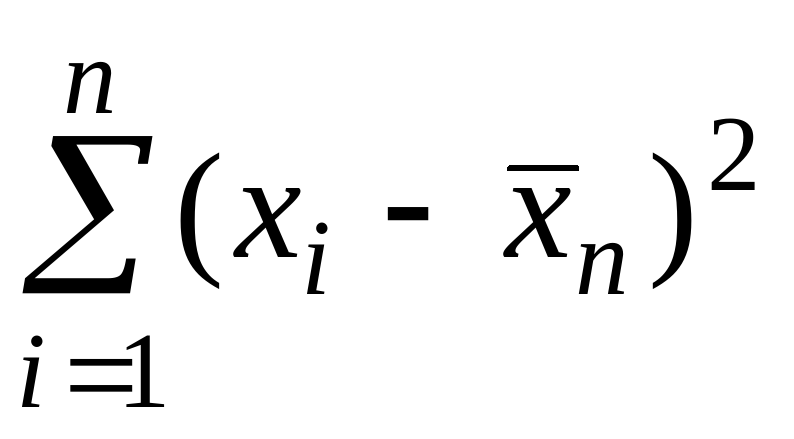 ) / n. Если же значения признака x1 , x2 ,…xk имеют соответственно частоты n1, n2, …nk, причем n1 + n2 +… + nk = n, то Dn=(
) / n. Если же значения признака x1 , x2 ,…xk имеют соответственно частоты n1, n2, …nk, причем n1 + n2 +… + nk = n, то Dn=( )/n (2), то есть выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
)/n (2), то есть выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии  (3).
(3).
Вычисление дисперсии, безразлично – выборочной или генеральной, можно упростить, используя следующую теорему.
Теорема [1].
Дисперсия равна среднему квадратов значений признака минус квадрат общей средней: D=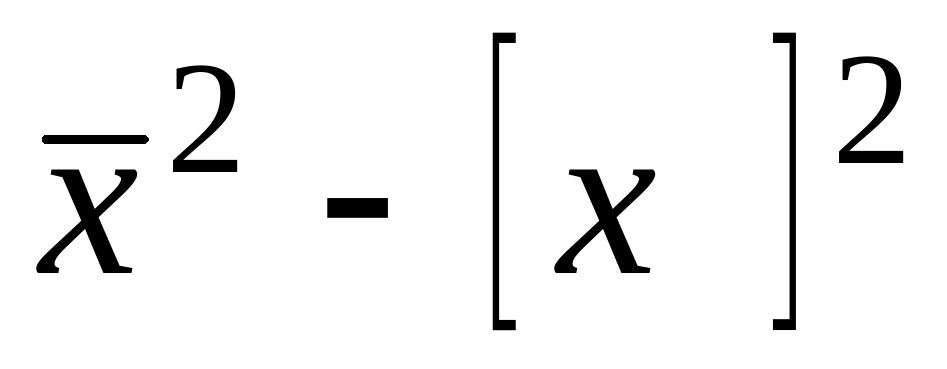 .
.
Выборочный коэффициент корреляции [1],[2].
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или несколько других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X, а затем от нескольких величин.
Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин. Под «общими» здесь подразумеваются такие факторы, которые воздействуют и на Y и на X. В этом случае возникает статистическая зависимость.
Например, если Y зависит от случайных факторов Z1, Z2, V1, V2, а X зависит от случайных факторов Z1, Z2, U1, то между Y и X имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: Z1 и Z2.
Статистической называют зависимость, при которой значение одной из величин влечет изменения распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.
Выборочный коэффициент корреляции определяется равенством
rn = 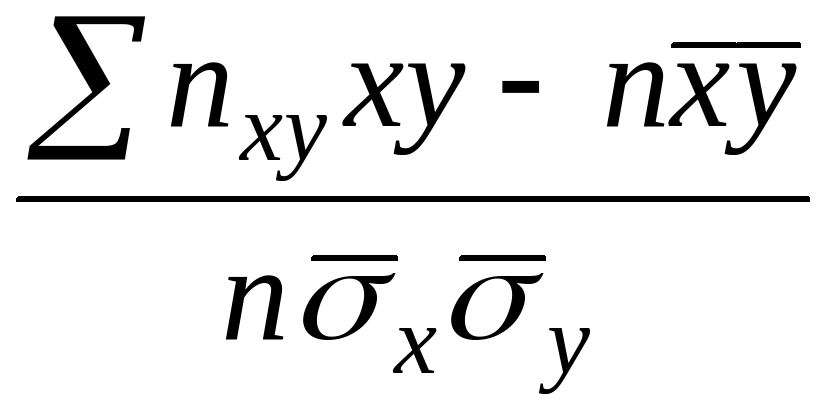 (4), где x, y – варианты (наблюдавшиеся значения) признаков X и Y; nxy – частота пары вариант (x,y); n – объем выборки (сумма всех частот); - выборочные средние. Известно, что если величины Y и X независимы, то коэффициент корреляции r = 0; если r = 1, то Y и X связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции r измеряет силу (тесноту) линейной связи между Y и X.
(4), где x, y – варианты (наблюдавшиеся значения) признаков X и Y; nxy – частота пары вариант (x,y); n – объем выборки (сумма всех частот); - выборочные средние. Известно, что если величины Y и X независимы, то коэффициент корреляции r = 0; если r = 1, то Y и X связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции r измеряет силу (тесноту) линейной связи между Y и X.
По результатам годовых оценок и оценок ЕГЭ по математике выпускников средней школы № 31 г. Ростова-на-Дону за три года вычислим среднюю выборочную, среднее квадратичное отклонение, выборочный коэффициент корреляции. Построим гистограммы и эмпирическую функцию на основе оценок ЕГЭ, а также полигон частот по первичному баллу, полученному на ЕГЭ.
Рассмотрим результаты итоговой аттестации по математике выпускников МОУ СОШ № 31 2004 года и сравним годовые оценки и оценки Единого государственного экзамена (см. приложение № 1).
Из таблицы видно, что результаты по математике за год следующие: «5» - 4, «4» - 21, «3» - 23; оценки по ЕГЭ: «5» - 10, «4» - 19, «3» - 12, «2» - 7. Учитывая, что выпускников 48, имеем объем выборки n=48, по результатам года:
варианты xi : 2 3 4 5
частоты ni: 0 23 21 4;
по результатам ЕГЭ:
варианты yi : 2 3 4 5
частоты ni: 7 12 19 10.
Вычислим общую среднюю годовых оценок по формуле (1):  =3,604167, по той же формуле вычислим общую среднюю оценок по ЕГЭ =3,666667.
=3,604167, по той же формуле вычислим общую среднюю оценок по ЕГЭ =3,666667.
Выборочное среднее квадратичное отклонение вычислим по формулам (2) и (3). По результатам за год =0,643778, по результатам ЕГЭ =0,974861.
Выборочный коэффициент корреляции rn вычислим по формуле (4): rn=0,632834.
Гистограмма, построенная на основе оценок, полученных на ЕГЭ, отображена в приложении № 3.
Построим эмпирическую функцию по данному распределению выборки.
Результаты ЕГЭ-2004 по математике:
| варианты xi | «2» | «3» | «4» | «5» |
| частоты ni | 7 | 12 | 19 | 10 |
Решение. Найдем объем выборки: 7+12+19+10=48. Наименьшая варианта равна 2, следовательно, F*(x)=0 при х =2. Значение х 3, т.е. х1 =2 наблюдалось 7 раз, следовательно, F*(х)=7/48 при 2=х3. Значение х 4, а именно х1 = 2, х2 = 3, наблюдалось 7+12=19 раз, следовательно, F*(х)=19/48 при 3 = х 4. Значение х 5 , а именно, х1=7, х2=12, х3=19, наблюдалось 7+12+19=38 раз, следовательно, F*(х)=38/48 при 4 =х Решение. Найдем объем выборки: 4+7+12+9=32. Наименьшая варианта равна 2, следовательно, F*(x)=0 при х =2. Значение х 3, т.е. х1 =2 наблюдалось 4 раза, следовательно, F*(х)=4/32=1/8=0,125. Значение х 4, а именно х1 = 2, х2 = 3, наблюдалось 4+7=11 раз, следовательно, F*(х)=11/32=0,34375 при 3 = х 4. Значение х 5 , а именно, х1=4, х2=7, х3=12 , наблюдалось 4+7+12=23 раза, следовательно, F*(х)=23/32=0,71875 при 4=х5. Так как х=5 – наибольшая варианта, то F*(х)=1 при х5.
5. Так как х=5 – наибольшая варианта, то F*(х)=1 при х5.
Полигон частот построим, учитывая первичный балл на ЕГЭ. Из таблицы результатов 2004 года видно, что наивысший первичный балл 32 получил Некрасов и такой результат один, самый маленький первичный балл – 4, его также получил один человек. Если за xi взять первичный балл учащихся, а за ni частоту его появления, то таблица для построения полигона частот выглядит так:
| xi | 32 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 7 | 6 | 5 | 4 |
| ni | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 2 | 3 | 4 | 6 | 2 | 4 | 3 | 2 | 5 | 1 | 2 | 1 | 3 | 1 |
График показан в приложении № 2.
Рассмотрим годовые оценки и результаты ЕГЭ по математике выпускников той же школы 2005 года (см. приложение № 1).
Пусть варианты xi – оценки за год, частоты ni – количество «2», «3», «4» и «5», варианты yi – оценки по ЕГЭ, объем выборки n=44 – количество выпускников.
Имеем за год: xi 2 3 4 5
ni 0 19 21 4. Вычисляем выборочную среднюю по формуле (1):  =3,659091, выборочное среднее отклонение по формулам (2) и (3): = 0,644951.
=3,659091, выборочное среднее отклонение по формулам (2) и (3): = 0,644951.
По итогам ЕГЭ: yi 2 3 4 5
ni 3 14 18 9. Вычисляем выборочную среднюю по формуле (1): =3,75, выборочное среднее отклонение по формулам (2) и (3): = 0,866025. Выборочный коэффициент корреляции rn вычислим по формуле (4): rn=0,718229.
Гистограмма оценок ЕГЭ 2005 года по математике показана в приложении № 3.
Построим эмпирическую функцию по данному распределению выборки (результаты выпускников 2005 года на ЕГЭ по математике).
ЕГЭ-2005
| варианты xi | «2» | «3» | «4» | «5» |
| частоты ni | 3 | 14 | 18 | 9 |
Решение. Найдем объем выборки: 3+14+18+9=44. Наименьшая варианта равна 2, следовательно, F*(x)=0 при х =2. Значение х 3, т.е. х1 =2 наблюдалось 3 раза, следовательно, F*(х)=3/44 при 2 = х 3. Значение х 4, а именно х1 = 2, х2 = 3, наблюдалось 3+14=17 раз, следовательно, F*(х)=17/44 при 3 = х 4. Значение х 5 , а именно, х1=3, х2=14, х3=18 , наблюдалось 3+14+18=35 раз, следовательно, F*(х)=35/44875 при 4=х5. Так как х=5 – наибольшая варианта, то F*(х)=1 при х5.
Полигон частот построим с учетом первичного балла.
Занесем в первую строку таблицы первичный балл (xi), а во вторую строку частоту появления этого балла на ЕГЭ (ni):
| xi | 28 | 27 | 26 | 23 | 22 | 21 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 5 | 2 |
| ni | 1 | 1 | 1 | 2 | 3 | 1 | 3 | 1 | 2 | 4 | 4 | 2 | 1 | 2 | 4 | 3 | 2 | 1 | 3 | 2 | 1 |
График показан в приложении № 2.
С 2006 года экзамен по математике в форме ЕГЭ не стал обязательным, а только для тех учащихся, кому он нужен для поступления в высшие учебные заведения. Тем не менее, 32 человека из 58 выпускников выбрали именно такую форму итоговой аттестации. Рассмотрим результаты прошлого года (см. приложение № 1).
Годовые оценки: xi 2 3 4 5
ni 0 13 13 6. Выборочная средняя -  =3,8125, выборочное среднее отклонение - =0,737804.
=3,8125, выборочное среднее отклонение - =0,737804.
Оценки по ЕГЭ yi 2 3 4 5
ni 4 7 12 9. Выборочная средняя =3,8125, выборочное среднее отклонение =0,997982. Выборочный коэффициент корреляции rn вычислим по формуле (4): rn=0,520245.
Гистограмму оценок ЕГЭ по математике прошлого года можно посмотреть в приложении № 3.
Построим эмпирическую функцию по данному распределению выборки (результаты выпускников 2006 года на ЕГЭ по математике).
ЕГЭ-2006
| варианты xi | «2» | «3» | «4» | «5» |
| частоты ni | 4 | 7 | 12 | 9 |
Решение. Найдем объем выборки: 4+7+12+9=32. Наименьшая варианта равна 2, следовательно, F*(x)=0 при х =2. Значение х 3, т.е. х1 =2 наблюдалось 4 раза, следовательно, F*(х)=4/32=1/8=0,125 при 2 = х 3. Значение х 4, а именно х1 = 2, х2 = 3, наблюдалось 4+7=11 раз, следовательно, F*(х)=11/32=0,34375 при 3 = х 4. Значение х 5 , а именно, х1=4, х2=7, х3=12 , наблюдалось 4+7+12=23 раза, следовательно, F*(х)=23/32=0,71875 при 4=х5. Так как х=5 – наибольшая варианта, то F*(х)=1 при х5.
Полигон частот построим с учетом первичного балла на ЕГЭ.
Занесем в первую строку таблицы первичный балл (xi), а во вторую строку частоту появления этого балла на ЕГЭ (ni):
| xi | 26 | 24 | 22 | 20 | 19 | 18 | 17 | 16 | 14 | 13 | 12 | 14 | 13 | 11 | 8 | 7 | 6 | 5 | 4 |
| ni | 1 | 1 | 5 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 4 | 2 | 1 | 2 | 1 |
График показан в приложении № 2.
Выводы.
На основании статистических расчетов можно сделать следующий вывод: значение коэффициента корреляции между годовыми оценками и оценками по ЕГЭ по математике в 2004 году равно приблизительно 0,6, в 2005 году — 0,7, в 2006 году — 0,5. Этот коэффициент достаточно велик, что свидетельствует о присутствии здесь статистической зависимости. В результате трехлетнего наблюдения выяснилось, что особых расхождений в величине найденного коэффициента корреляции не оказалось, несмотря на то, что на эту величину влияли различные факторы. Тем не менее, это говорит о достоверности результатов. Следует отметить, что необходимо продолжить статистический анализ в данном направлении и дальше, чтобы выяснить основные закономерности исследуемых зависимостей. Это можно сделать лишь при достаточно длительных наблюдениях.
Приложение 1
Результаты за год и по ЕГЭ выпускников МОУ СОШ № 31 по математике.
2004 год
| № п/п | Фамилия | Годовая оценка | Оценка по ЕГЭ | Первичный балл | Класс |
| 1 | Балык | 3 | 5 | 22 | 11А |
| 2 | Гордеев | 4 | 4 | 18 | 11А |
| 3 | Деникова | 5 | 5 | 22 | 11А |
| 4 | Дружинина | 4 | 4 | 19 | 11А |
| 5 | Зинченко | 3 | 5 | 20 | 11А |
| 6 | Каплунова | 4 | 4 | 18 | 11А |
| 7 | Карапетян | 3 | 3 | 10 | 11А |
| 8 | Картавик | 3 | 2 | 5 | 11А |
| 9 | Китанин | 3 | 3 | 9 | 11А |
| 10 | Ковалевская | 3 | 3 | 10 | 11А |
| 11 | Костина | 3 | 2 | 4 | 11А |
| 12 | Кузнецов | 3 | 3 | 11 | 11А |
| 13 | Купина | 5 | 5 | 25 | 11А |
| 14 | Курочкин | 4 | 3 | 12 | 11А |
| 15 | Кучерук | 4 | 4 | 12 | 11А |
| 16 | Лариш | 3 | 3 | 10 | 11А |
| 17 | Майорова | 5 | 5 | 24 | 11А |
| 18 | Матушкин | 4 | 4 | 15 | 11А |
| 19 | Михайленко | 4 | 4 | 18 | 11А |
| 20 | Парада | 5 | 5 | 25 | 11А |
| 21 | Пилипчук | 3 | 3 | 6 | 11А |
| 22 | Процик | 3 | 2 | 5 | 11А |
| 23 | Сечкова | 4 | 4 | 14 | 11А |
| 24 | Столяров | 4 | 4 | 19 | 11А |
| 25 | Шкоденко | 4 | 5 | 21 | 11А |
| 26 | Александрова | 3 | 2 | 4 | 11Б |
| 27 | Бугаев | 3 | 3 | 7 | 11Б |
| 28 | Валькова | 3 | 4 | 12 | 11Б |
| 29 | Ватулина | 4 | 3 | 11 | 11Б |
| 30 | Вербенко | 4 | 4 | 15 | 11Б |
| 31 | Галич | 3 | 3 | 7 | 11Б |
| 32 | Гоптарева | 4 | 4 | 13 | 11Б |
| 33 | Гордиенко | 4 | 4 | 16 | 11Б |
| 34 | Гришкина | 4 | 5 | 23 | 11Б |
| 35 | Ефремов | 3 | 2 | 5 | 11Б |
| 36 | Зенкин | 4 | 4 | 13 | 11Б |
| 37 | Казачков | 3 | 2 | 5 | 11Б |
| 38 | Некрасов | 4 | 5 | 32 | 11Б |
| 39 | Ольховская | 3 | 3 | 10 | 11Б |
| 40 | Писарев | 4 | 4 | 16 | 11Б |
| 41 | Приходько | 4 | 4 | 13 | 11Б |
| 42 | Рукас | 4 | 4 | 15 | 11Б |
| 43 | Семенова | 3 | 2 | 5 | 11Б |
| 44 | Соловьев | 3 | 5 | 25 | 11Б |
| 45 | Федоренко | 4 | 4 | 16 | 11Б |
| 46 | Фомичев | 3 | 4 | 15 | 11Б |
| 47 | Цыганкова | 3 | 4 | 15 | 11Б |
| 48 | Юрковец | 3 | 3 | 10 | 11Б |
|
|
| 3,604167 | 3,666667 | среднее |
|
|
|
| 0,643778 | 0,974861 | стандарт откл Пирсона |
|
|
| 0,632834 |
| Коэф коррел |
2005 год
| № п/п | Фамилия | Оценка за год | Оценка по ЕГЭ | Первичный балл | Класс |
| 1 | Анищенко | 5 | 4 | 23 | 11А |
| 2 | Белая | 3 | 4 | 15 | 11А |
| 3 | Бельцева | 3 | 3 | 8 | 11А |
| 4 | Воробьева | 4 | 4 | 17 | 11А |
| 5 | Воскобойникова | 3 | 3 | 9 | 11А |
| 6 | Евсина | 4 | 4 | 15 | 11А |
| 7 | Каплунова | 4 | 5 | 22 | 11А |
| 8 | Левченко | 5 | 5 | 28 | 11А |
| 9 | Мальцева | 3 | 4 | 13 | 11А |
| 10 | Меликсетян | 4 | 5 | 23 | 11А |
| 11 | Навалихина | 3 | 3 | 9 | 11А |
| 12 | Невзорова | 4 | 4 | 14 | 11А |
| 13 | Недвигин | 3 | 4 | 12 | 11А |
| 14 | Осипов | 3 | 3 | 11 | 11А |
| 15 | Позднышева | 3 | 2 | 2 | 11А |
| 16 | Пономарев | 4 | 4 | 19 | 11А |
| 17 | Струкова | 3 | 3 | 11 | 11А |
| 18 | Тягун | 3 | 3 | 10 | 11А |
| 19 | Усачев | 4 | 3 | 10 | 11А |
| 20 | Шестакова | 4 | 5 | 22 | 11А |
| 21 | Аллало | 4 | 4 | 16 | 11Б |
| 22 | Беляев | 5 | 5 | 27 | 11Б |
| 23 | Геворгян | 3 | 3 | 7 | 11Б |
| 24 | Гришкина | 4 | 4 | 17 | 11Б |
| 25 | Давиденко | 3 | 3 | 7 | 11Б |
| 26 | Даниелян | 3 | 2 | 5 | 11Б |
| 27 | Ефимов | 4 | 4 | 19 | 11Б |
| 28 | Земцова | 4 | 4 | 15 | 11Б |
| 29 | Каптуревская | 4 | 4 | 15 | 11Б |
| 30 | Коваленко | 4 | 3 | 11 | 11Б |
| 31 | Кондрашев | 3 | 4 | 16 | 11Б |
| 32 | Коротнев | 4 | 4 | 14 | 11Б |
| 33 | Костенко | 4 | 5 | 21 | 11Б |
| 34 | Кузьмищенко | 4 | 4 | 16 | 11Б |
| 35 | Куценко | 3 | 3 | 12 | 11Б |
| 36 | Лисовенко | 3 | 3 | 11 | 11Б |
| 37 | Миктадова | 4 | 4 | 18 | 11Б |
| 38 | Петренко | 3 | 3 | 10 | 11Б |
| 39 | Попова | 4 | 5 | 19 | 11Б |
| 40 | Савченко | 3 | 3 | 7 | 11Б |
| 41 | Сазонов | 5 | 5 | 26 | 11Б |
| 42 | Скляренко | 3 | 2 | 5 | 11Б |
| 43 | Старчук | 4 | 4 | 16 | 11Б |
| 44 | Шевкунов | 4 | 5 | 22 | 11Б |
|
|
| 3,659091 | 3,75 | среднее |
|
|
|
| 0,644951 | 0,866025 | стандарт откл Пирсона |
|
|
| 0,718229 |
| Коэф коррел |
2006 год
| № п/п | Фамилия | Оценка за год | Оценка по ЕГЭ | Первичный балл | Класс |
| 1 | Абанькин | 4 | 4 | 13 | 11А |
| 2 | Акопян | 4 | 4 | 14 | 11А |
| 3 | Алкидов | 3 | 2 | 4 | 11А |
| 4 | Андрющенко | 3 | 3 | 7 | 11А |
| 5 | Бабурина | 4 | 5 | 22 | 11А |
| 6 | Боев | 5 | 4 | 17 | 11А |
| 7 | Гергерт | 4 | 5 | 22 | 11А |
| 8 | Земнова | 3 | 2 | 6 | 11А |
| 9 | Калужников | 5 | 4 | 14 | 11А |
| 10 | Карташьян | 3 | 4 | 13 | 11А |
| 11 | Коломоец | 4 | 4 | 12 | 11А |
| 12 | Коркошко | 5 | 4 | 12 | 11А |
| 13 | Коцурова | 3 | 2 | 5 | 11А |
| 14 | Кузнецов | 3 | 4 | 16 | 11А |
| 15 | Леньков | 4 | 5 | 24 | 11А |
| 16 | Мальцев | 3 | 3 | 8 | 11А |
| 17 | Мельникова | 3 | 4 | 14 | 11А |
| 18 | Панченко | 5 | 5 | 20 | 11А |
| 19 | Пигунова | 4 | 4 | 14 | 11А |
| 20 | Соловьев | 3 | 3 | 7 | 11А |
| 21 | Уколова | 4 | 5 | 22 | 11А |
| 22 | Федоров | 4 | 5 | 19 | 11А |
| 23 | Чуднова | 4 | 5 | 26 | 11А |
| 24 | Шатилина | 5 | 5 | 22 | 11А |
| 25 | Александрова | 4 | 2 | 5 | 11Б |
| 26 | Болотный | 4 | 3 | 8 | 11Б |
| 27 | Быкова | 5 | 5 | 22 | 11Б |
| 28 | Гладков | 3 | 4 | 18 | 11Б |
| 29 | Замятин | 3 | 4 | 17 | 11Б |
| 30 | Косякова | 4 | 3 | 8 | 11Б |
| 31 | Масленников | 4 | 3 | 11 | 11Б |
| 32 | Шкляр | 3 | 3 | 8 | 11Б |
|
|
| 3,8125 | 3,8125 | среднее |
|
|
|
| 0,737804 | 0,997982 | стандарт откл Пирсона |
|
|
| 0,520245 |
| Коэф коррел. |
Приложение № 2.
Полигоны частот, составленные на основе первичного балла, полученного на ЕГЭ по математике выпускниками МОУ СОШ № 31.
Полигон частот (первичный балл на ЕГЭ-2006)
Полигон частот (первичный балл на ЕГЭ-2005)
Полигон частот (первичный балл ЕГЭ-2004)
Приложение № 3.
Гистограммы оценок, полученных на ЕГЭ по математике выпускниками
МОУ СОШ № 31.
Гистограмма (оценки на ЕГЭ-2006)
Гистограмма (оценки на ЕГЭ-2005)
Гистограмма (оценки на ЕГЭ-2004)
Литература.
Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. - М. Высшая школа, 1999.
Венцель Е.С. Теория вероятностей. М. Высшая школа. 2001.
Гренандер У. Случайные процессы и статистические выводы. М., Мир. 1961.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М. Высшая школа 1974.
Приложение № 4.
Эмпирические функции распределения.
2
















