Стереометрия. Многогранники

Математика - Стереометрия

• Многогранники

Преподаватель

Князева Светлана Евгеньевна

27.03.2020г.

• Стереометрия – это слово происходит от двух греческих слов «стерео» — объемный, пространственный и «метрео» — измерять.
• В стереометрии наряду с простейшими фигурами — точками, прямыми и плоскостями рассматриваются геометрические тела и их поверхности.

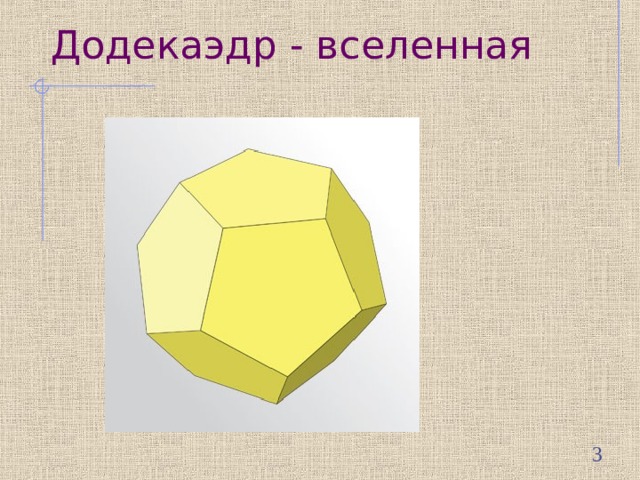
Додекаэдр - вселенная

Куб - земля

Пирамида - огонь

Икосаэдр - вода

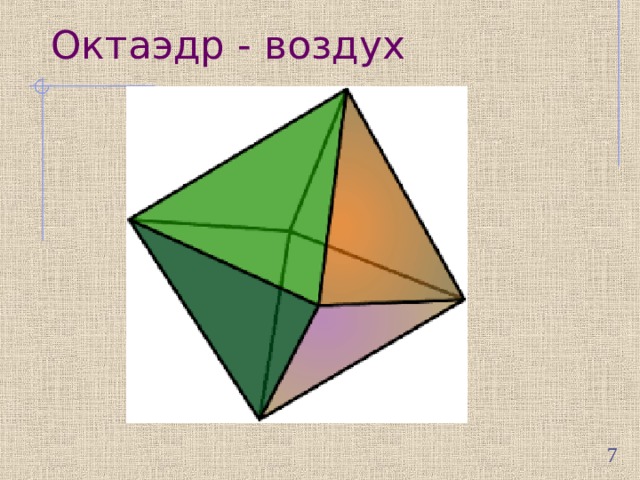
Октаэдр - воздух

Курносый куб

Пирамида

• Это многогранник, составленный из n – угольника и n треугольников, имеющих общую вершину

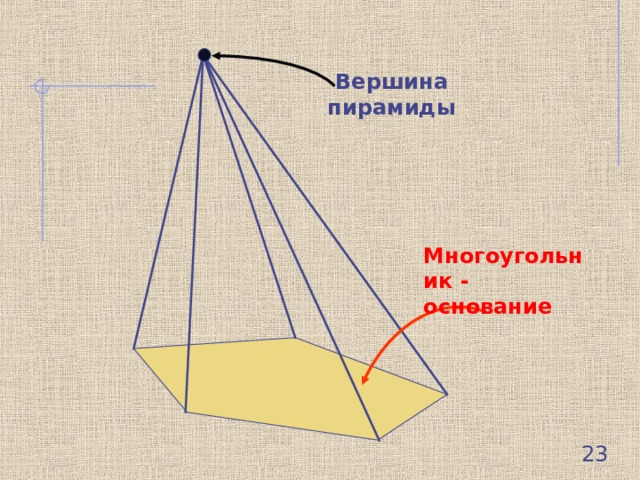
Вершина пирамиды

Многоугольник - основание

23

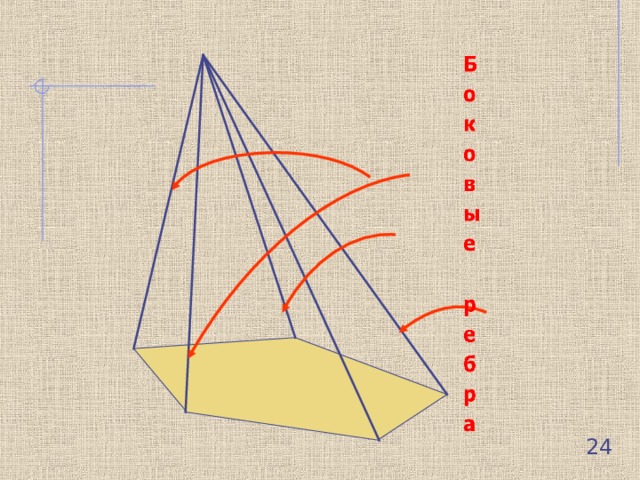
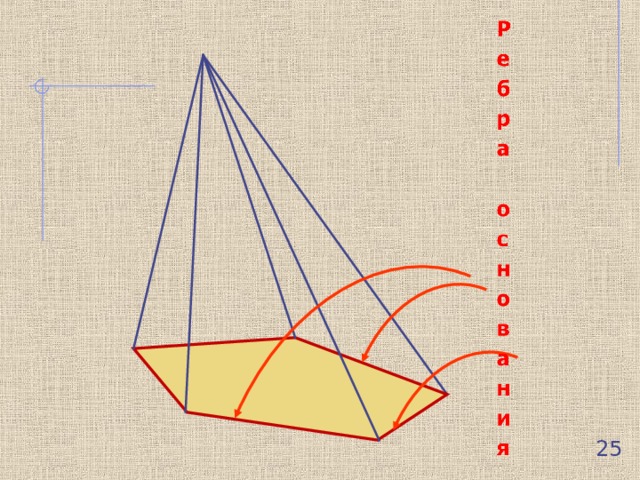
25

25

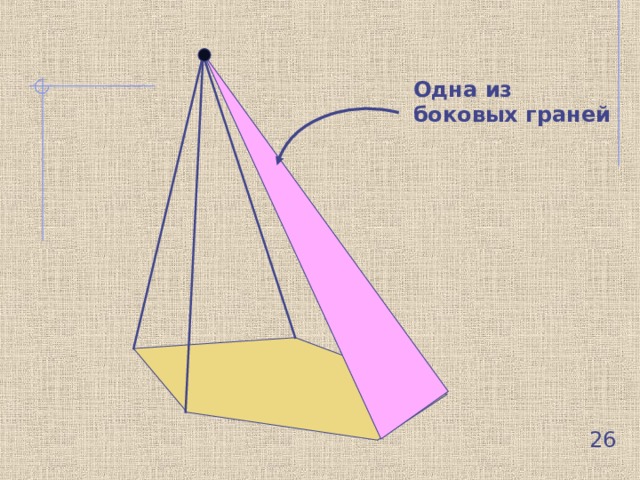
Одна из

боковых граней

26

Пирамиды, как правило называются по названию многоугольника, лежащего в основании.

26

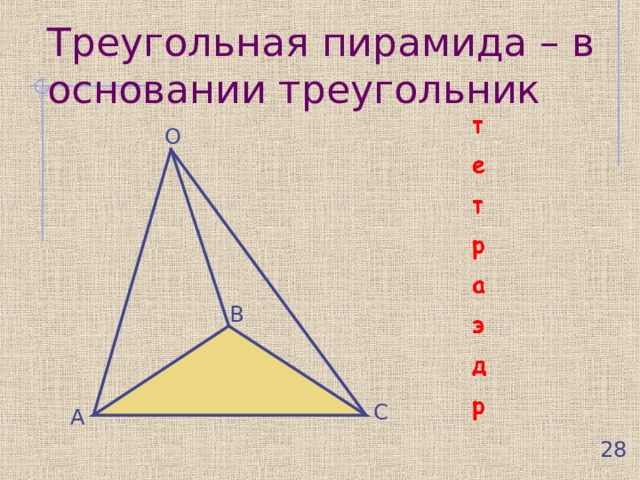
Треугольная пирамида – в основании треугольник

О

В

С

А

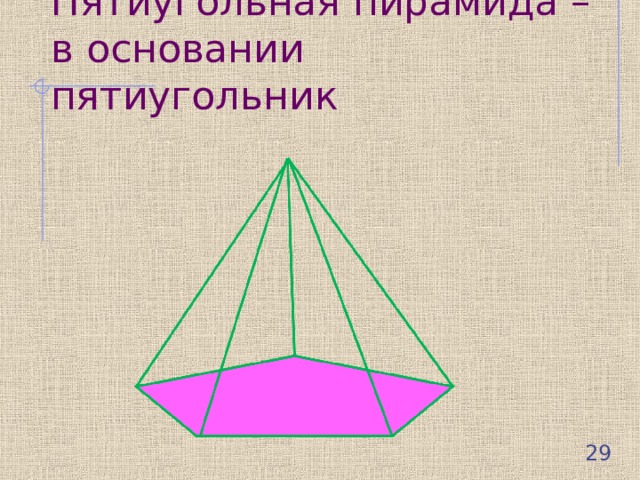
Пятиугольная пирамида – в основании пятиугольник

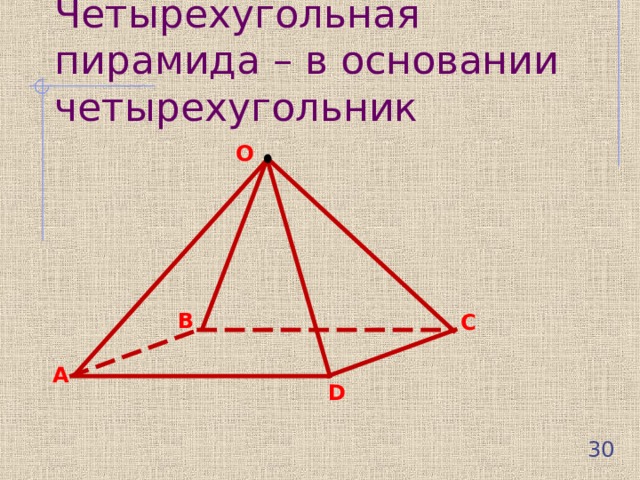
Четырехугольная пирамида – в основании четырехугольник

О

В

С

А

D

А

D

В

С

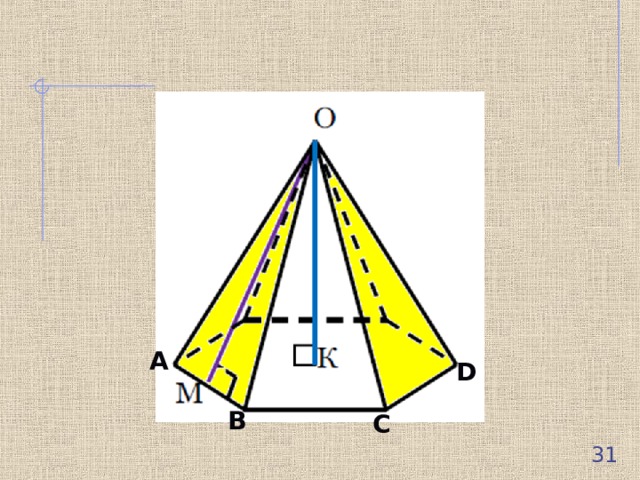
• Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания (ОК), является ее высотой.

Строим треугольную пирамиду. Шаг первый: изображаем треугольник

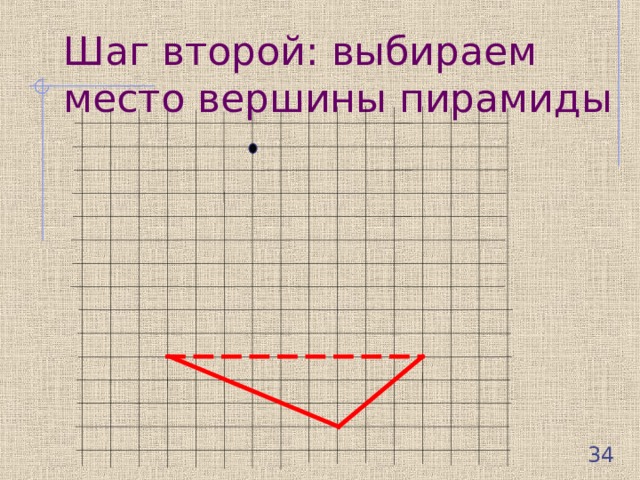
Шаг второй: выбираем место вершины пирамиды

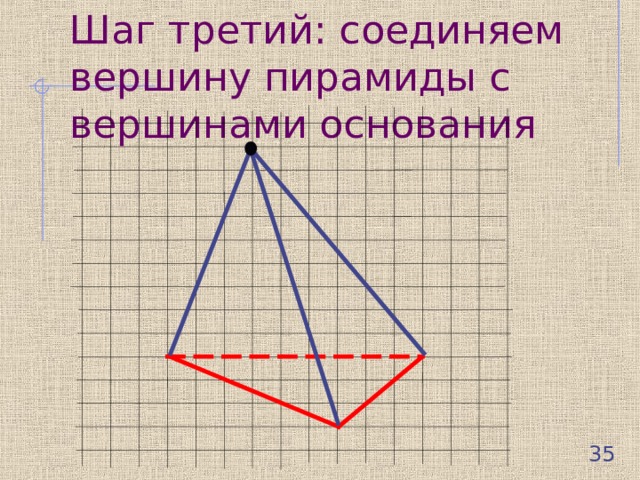
Шаг третий: соединяем вершину пирамиды с вершинами основания

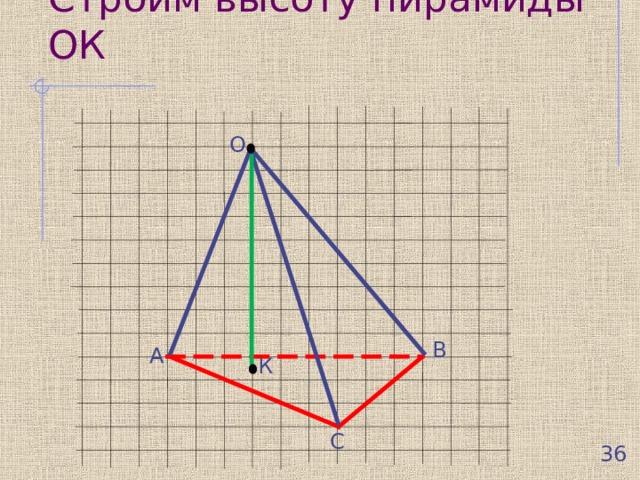
Строим высоту пирамиды ОК

О

В

А

К

С

36

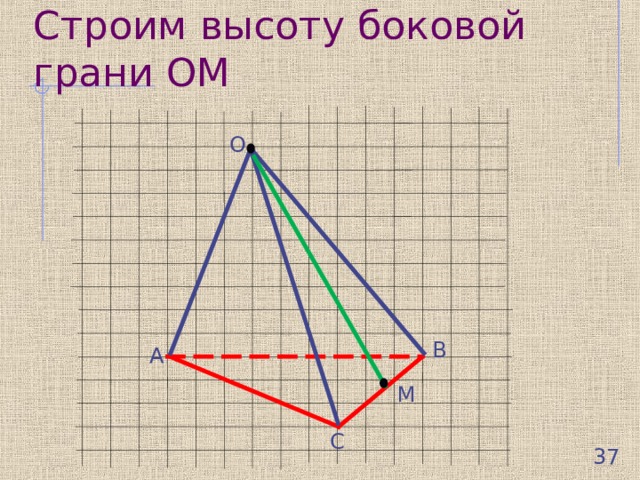
Строим высоту боковой грани ОМ

О

В

А

М

С

37

Строим четырехугольную пирамиду. Шаг первый: изображаем параллелограмм

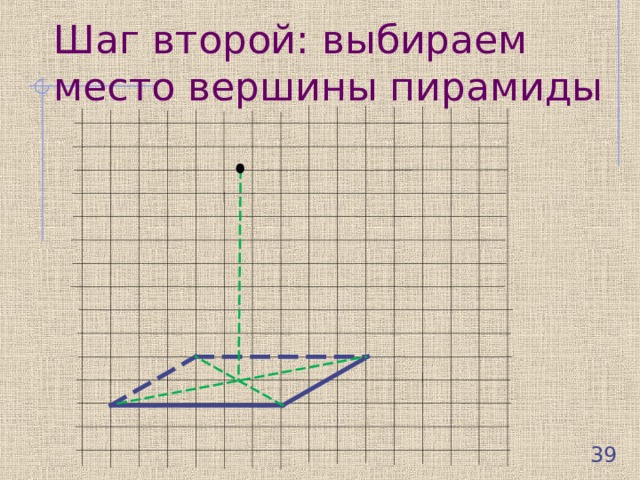
Шаг второй: выбираем место вершины пирамиды

39

Шаг третий: соединяем вершину пирамиды с вершинами основания

О

D

С

А

В

40

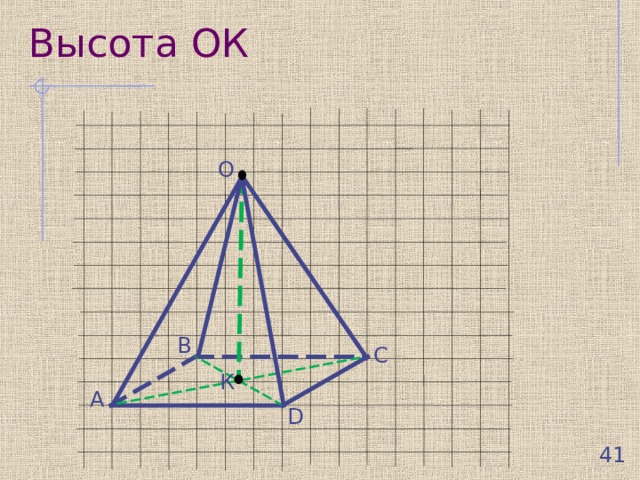
Высота ОК

O

В

С

К

А

D

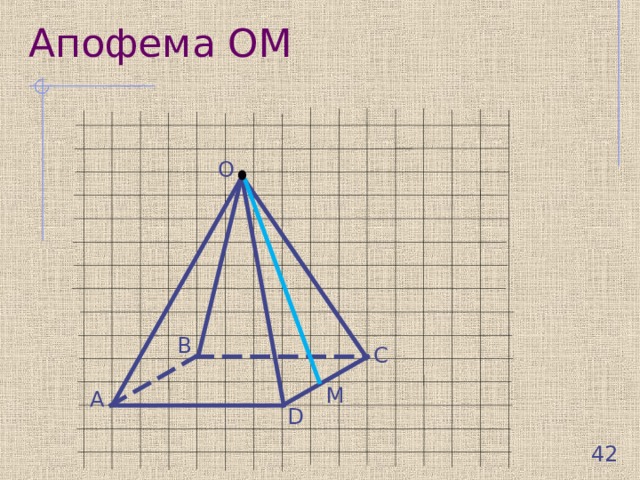
Апофема ОМ

O

В

С

М

А

D

42

ПРИЗМА

• n – угольной призмой называется многогранник, составленный из двух равных многоугольников лежащих в параллельных плоскостях, которые называются основаниями призмы и n параллелограммов, которые называются боковыми гранями призмы. Боковые ребра призмы равны и параллельны друг другу.

42

шестиугольная призма ABCDEF = A 1 B 1 C 1 D 1 E 1 F 1

С 1

В 1

А 1

D 1

F 1

Е

С

В

А

D

F

Е

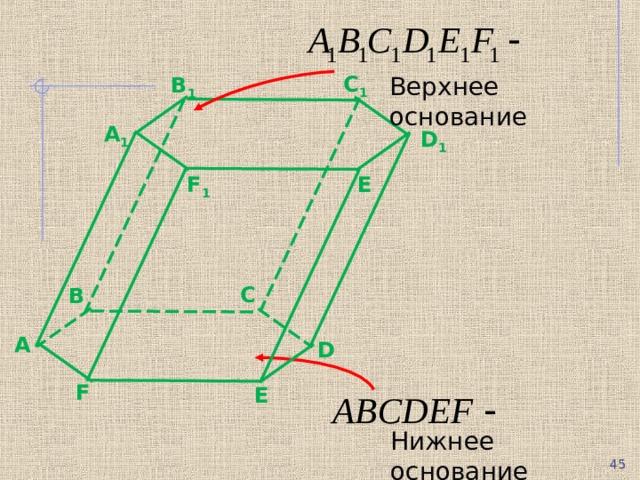
С 1

Верхнее основание

В 1

А 1

D 1

F 1

Е

С

В

А

D

F

Е

Нижнее основание

45

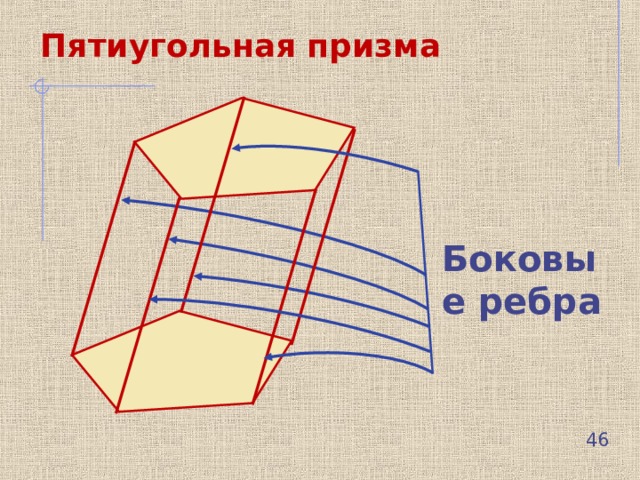
Пятиугольная призма

Боковые ребра

45

Ребра верхнего основания

47

Ребра нижнего основания

48

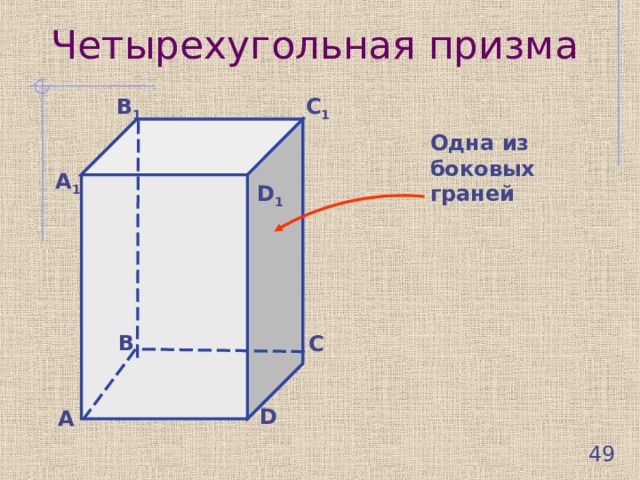
Четырехугольная призма

В 1

С 1

Одна из боковых

граней

А 1

D 1

В

С

D

А

Отрезок АВ, проведенный из произвольной точки одного основания, перпендикулярно к плоскости другого основания, называется высотой призмы. Все высоты призмы равны и параллельны друг другу.

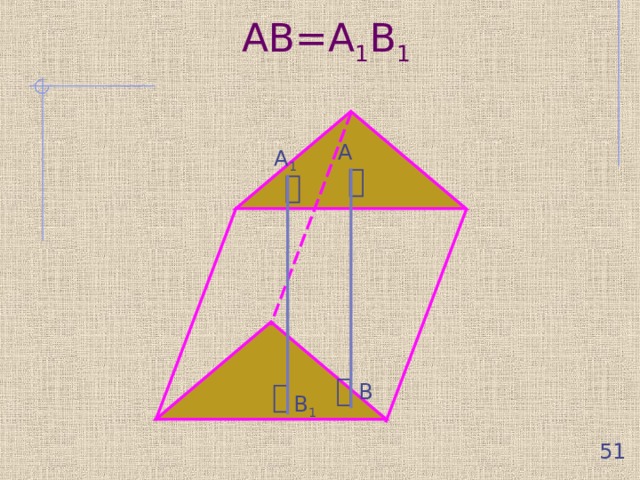
АВ=А 1 В 1

А

А 1

В

В 1

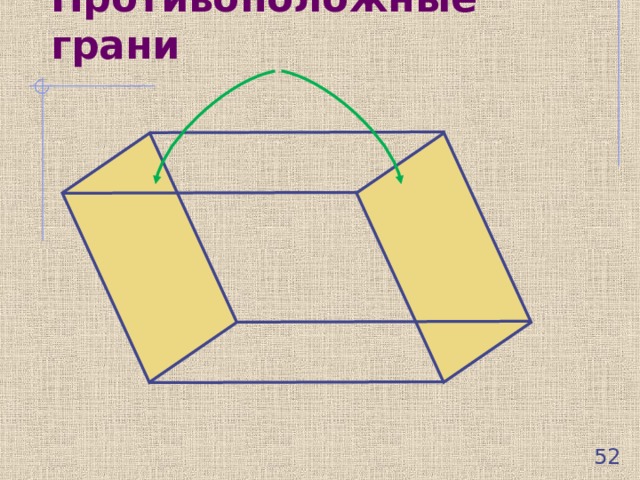
Противоположные грани

В 1

С 1

А 1

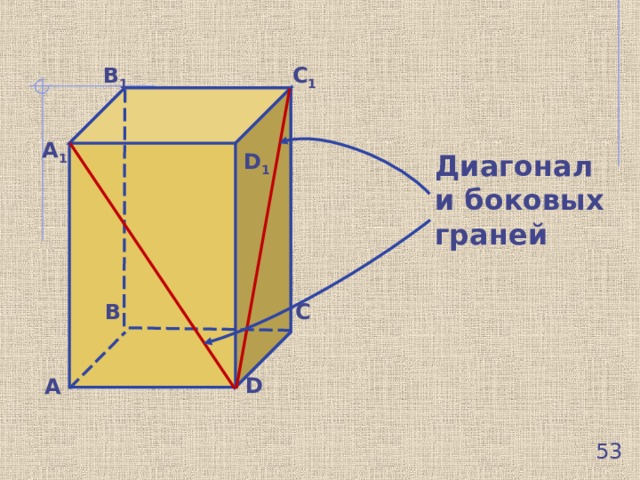
Диагонали боковых

граней

D 1

В

С

D

А

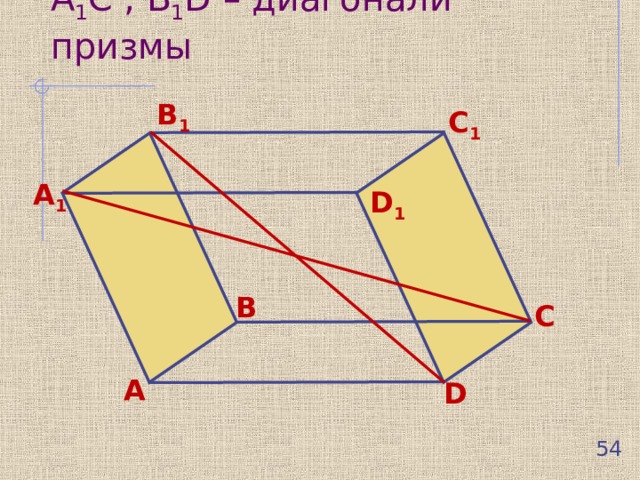
A 1 C , B 1 D – диагонали призмы

B 1

C 1

A 1

D 1

B

C

A

D

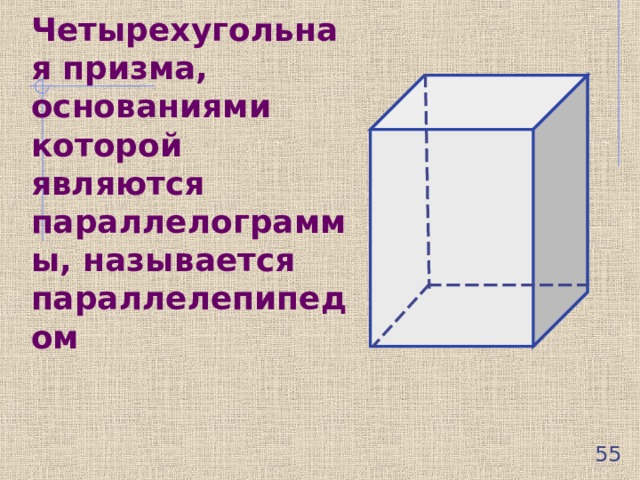
Четырехугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом

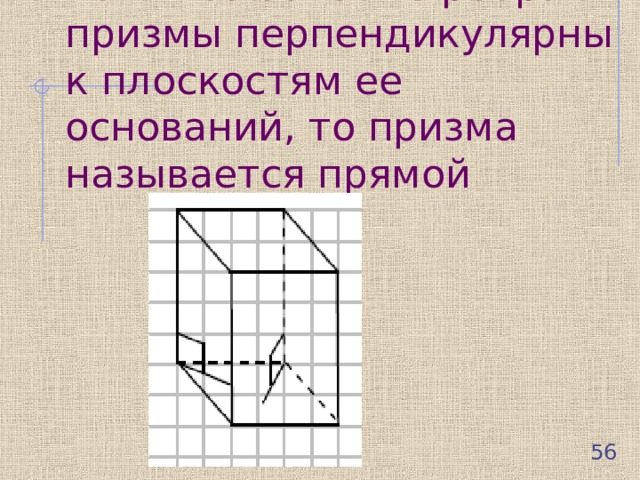
Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований, то призма называется прямой

• Прямая призма, основаниями которой являются правильные многоугольники, называется правильной.

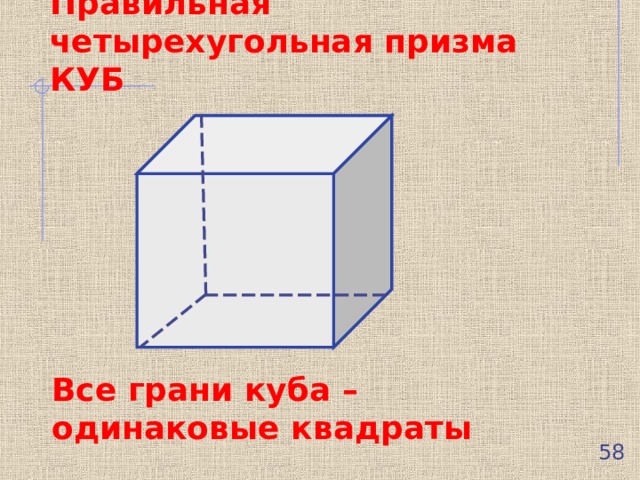
Правильная четырехугольная призма КУБ

Все грани куба – одинаковые квадраты

58

Строим прямую треугольную призму: строим два треугольника параллельно друг другу

Соединяем попарно вершины треугольников

В 1

С 1

А 1

В

С

А

60

Строим прямую четырехугольную призму: строим два параллелограмма параллельно друг другу

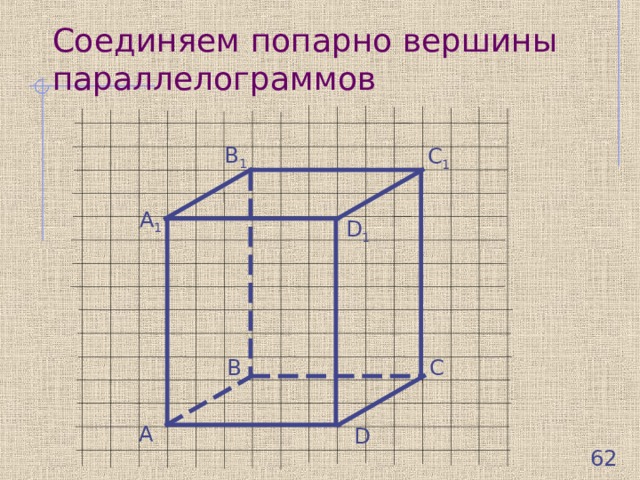
Соединяем попарно вершины параллелограммов

В 1

С 1

А 1

D 1

В

С

А

D

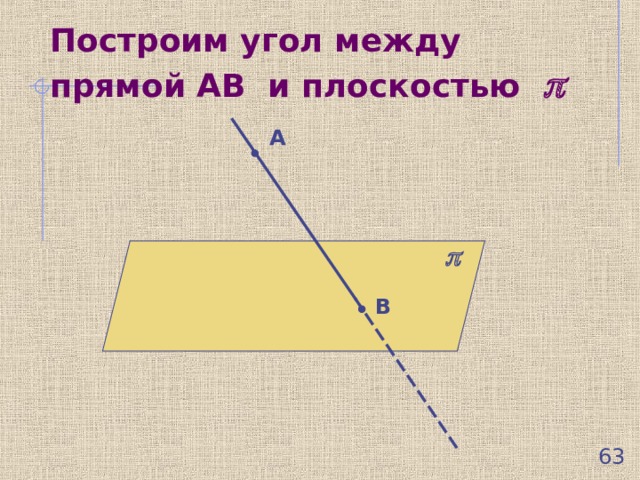
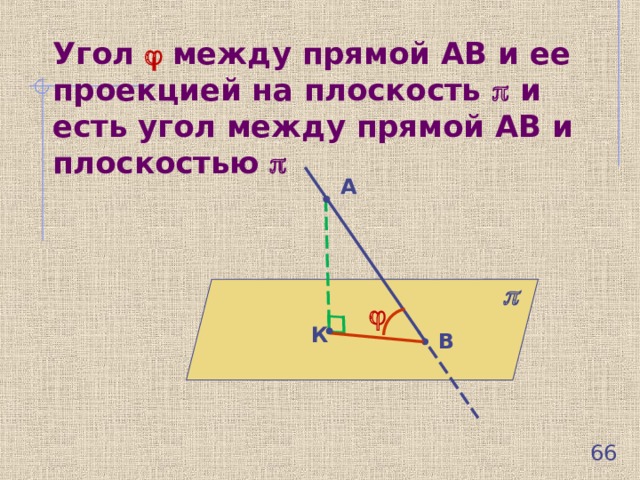
Построим угол между прямой АВ и плоскостью 

А



В

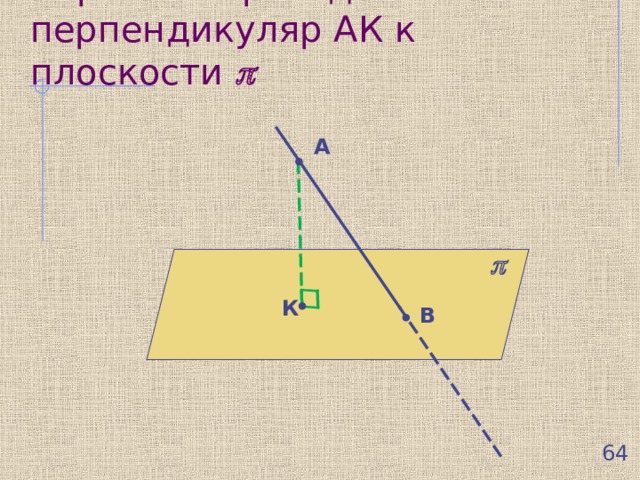
Через т.А проводим перпендикуляр АК к плоскости 

А



К

В

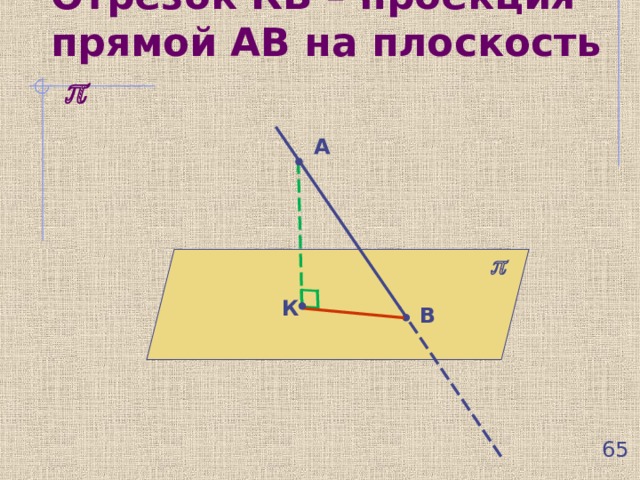
Отрезок КВ – проекция прямой АВ на плоскость 

А



К

В

А

Угол  между прямой АВ и ее проекцией на плоскость  и есть угол между прямой АВ и плоскостью 





К

В

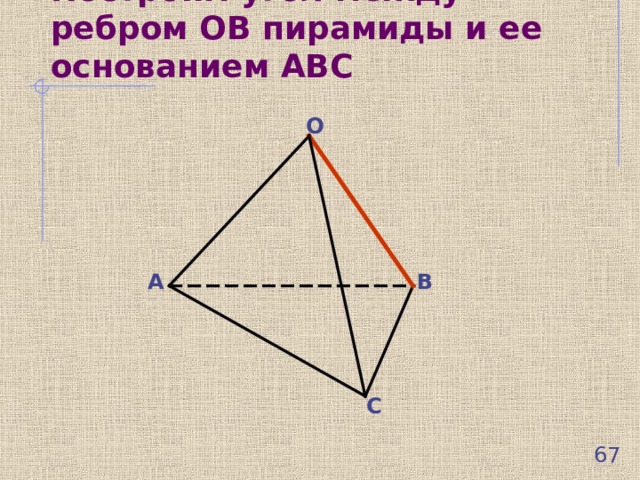
Построим угол между ребром ОВ пирамиды и ее основанием АВС

О

В

А

С

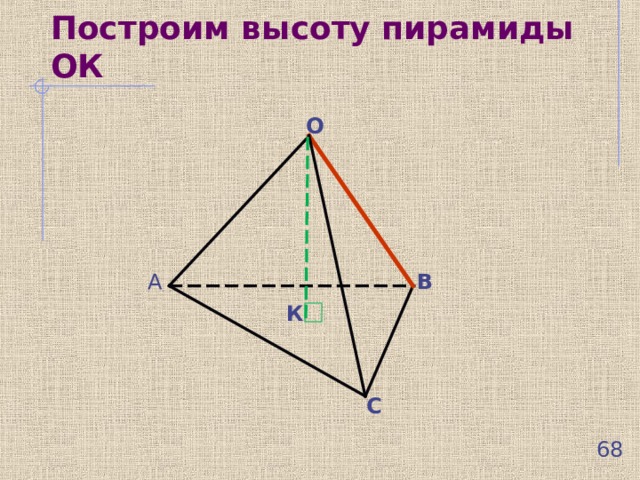
Построим высоту пирамиды ОК

О

В

А

К

С

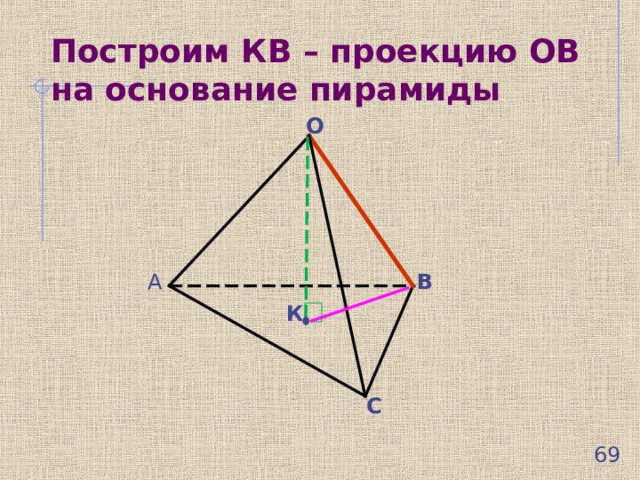
Построим КВ – проекцию ОВ на основание пирамиды

О

В

А

К

С

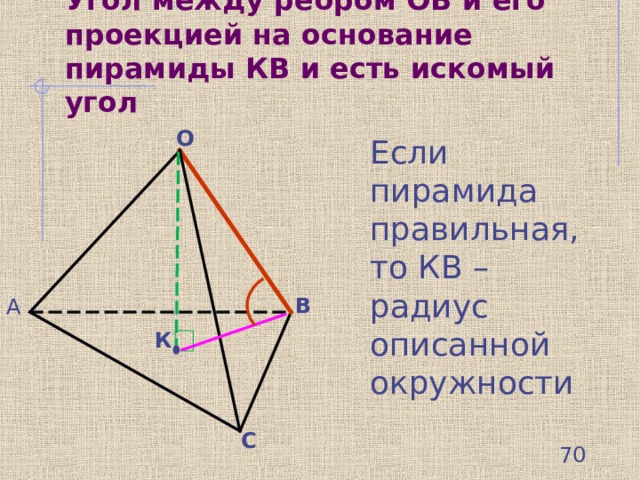
Угол между ребром ОВ и его проекцией на основание пирамиды КВ и есть искомый угол

О

Если пирамида правильная, то КВ – радиус описанной окружности

В

А

К

С

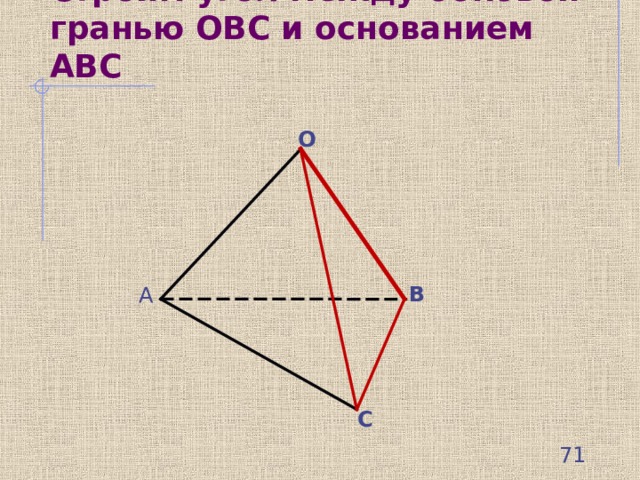
Строим угол между боковой гранью ОВС и основанием АВС

О

В

А

С

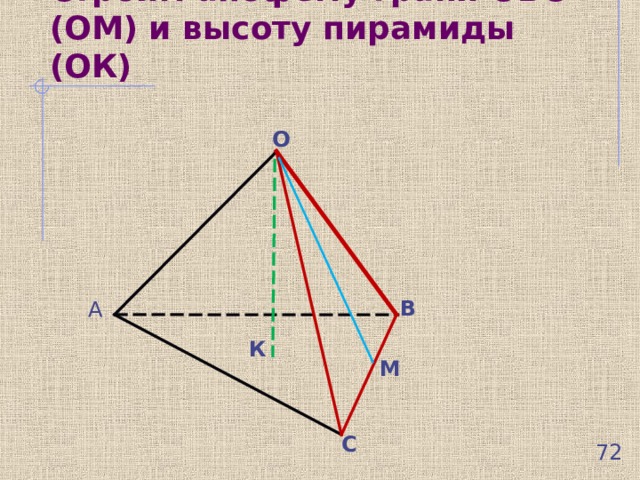
Строим апофему грани ОВС (ОМ) и высоту пирамиды (ОК)

О

В

А

К

М

С

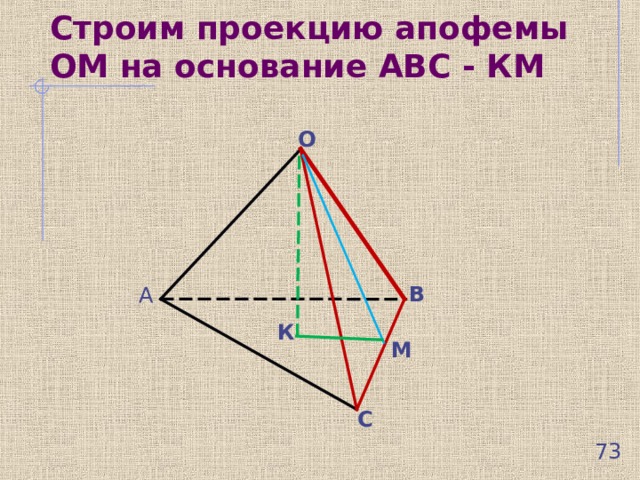
Строим проекцию апофемы ОМ на основание АВС - КМ

О

В

А

К

М

С

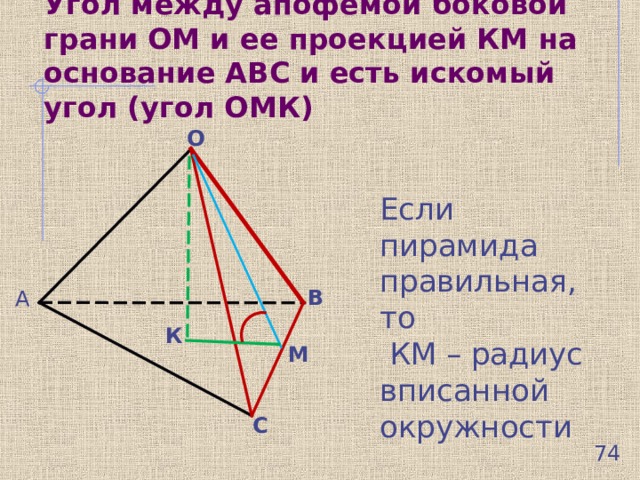
Угол между апофемой боковой грани ОМ и ее проекцией КМ на основание АВС и есть искомый угол (угол ОМК)

О

Если пирамида правильная, то КМ – радиус вписанной окружности

В

А

К

М

С