Стереометрия. Призма

Призма

КЭиФ

Преподаватель

Князева Светлана Евгеньевна

Основные вопросы лекции

• Призма и ее составляющие – повторение
• Основные формулы планиметрии – повторение
• Решение простейших задач на призму
• Боковая и полная поверхность призмы
• Объем призмы

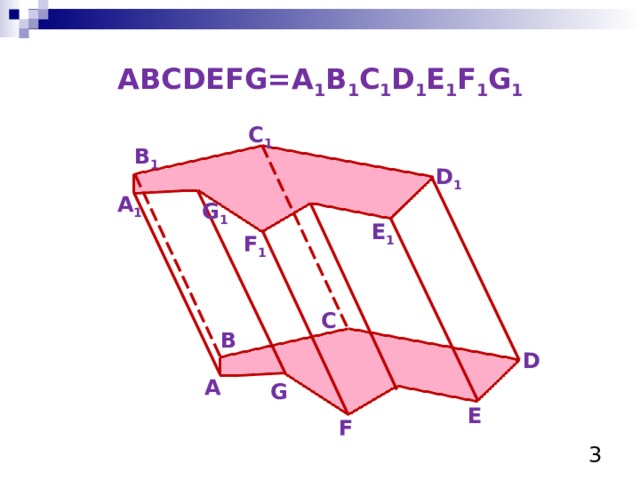
ABCDEFG=A 1 B 1 C 1 D 1 E 1 F 1 G 1

С 1

В 1

D 1

А 1

G 1

E 1

F 1

С

В

D

А

G

E

F

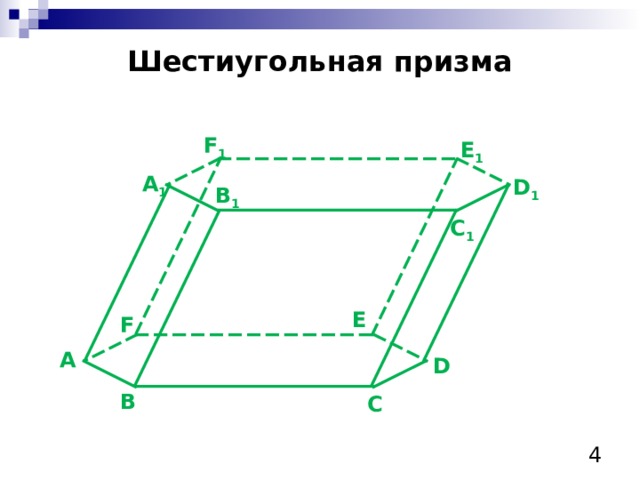
Шестиугольная призма

F 1

E 1

A 1

D 1

B 1

C 1

E

F

A

D

B

C

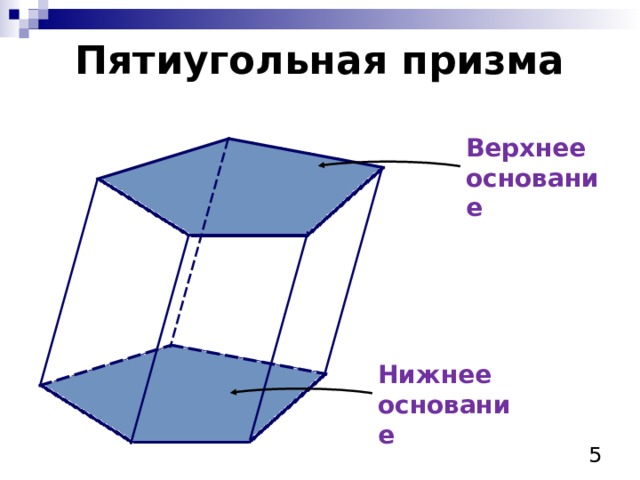
Пятиугольная призма

Верхнее основание

Нижнее основание

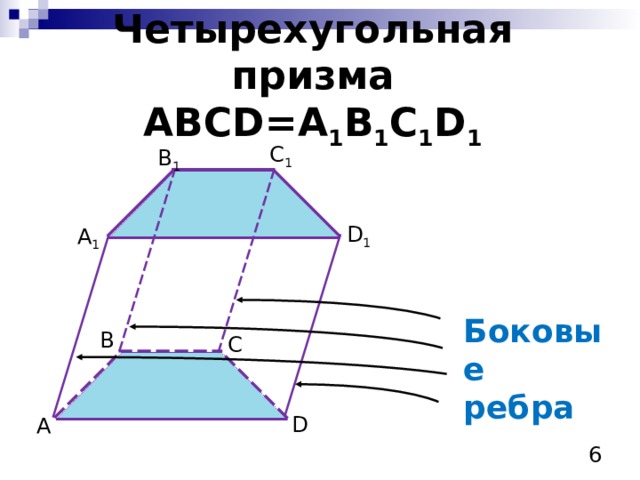
Четырехугольная призма ABCD=A 1 B 1 C 1 D 1

С 1

В 1

D 1

А 1

Боковые ребра

В

С

D

А

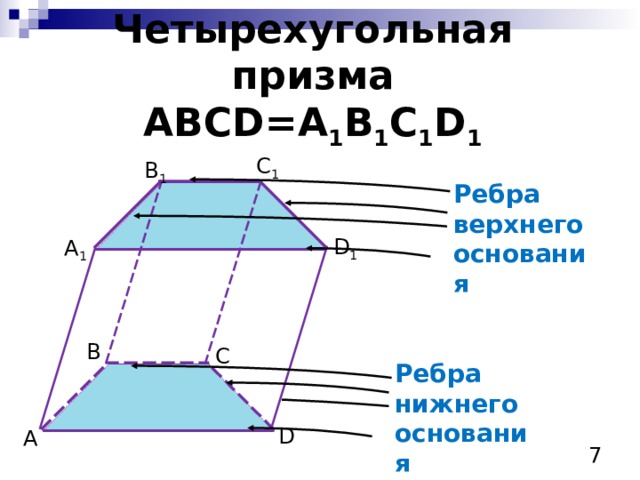
Четырехугольная призма ABCD=A 1 B 1 C 1 D 1

С 1

В 1

Ребра верхнего основания

D 1

А 1

В

С

Ребра нижнего основания

D

А

6

Четырехугольная призма

В 1

С 1

Одна из боковых

граней

А 1

D 1

В

С

D

А

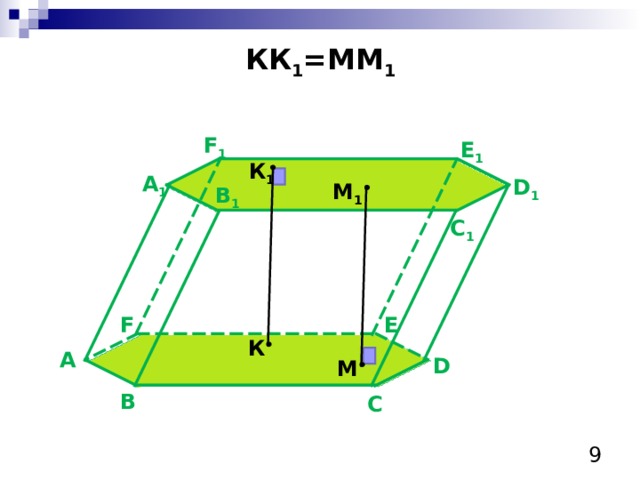
КК 1 =ММ 1

F 1

E 1

К 1

A 1

D 1

М 1

B 1

C 1

E

F

К

A

D

М

B

C

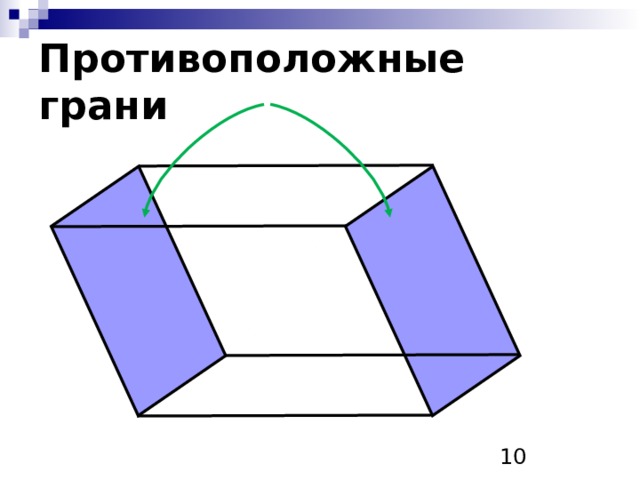
Противоположные грани

В 1

С 1

А 1

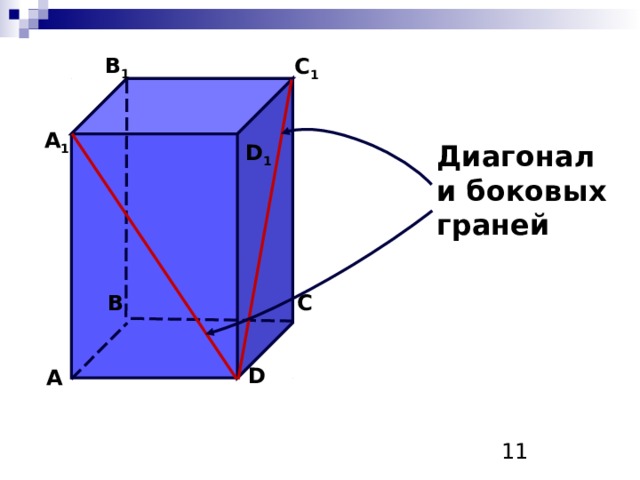
Диагонали боковых

граней

D 1

В

С

D

А

11

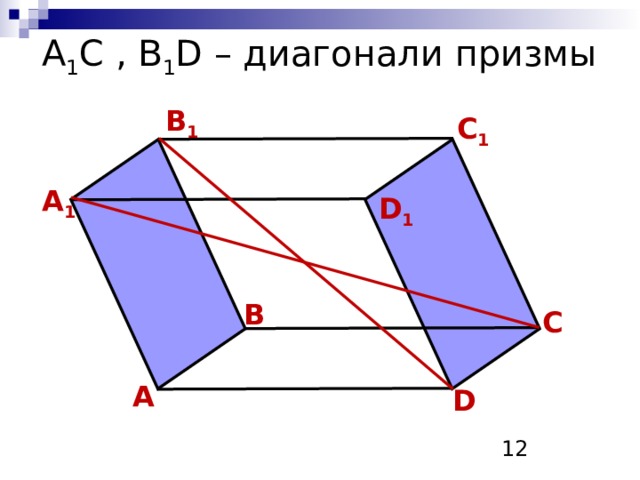
A 1 C , B 1 D – диагонали призмы

B 1

C 1

A 1

D 1

B

C

A

D

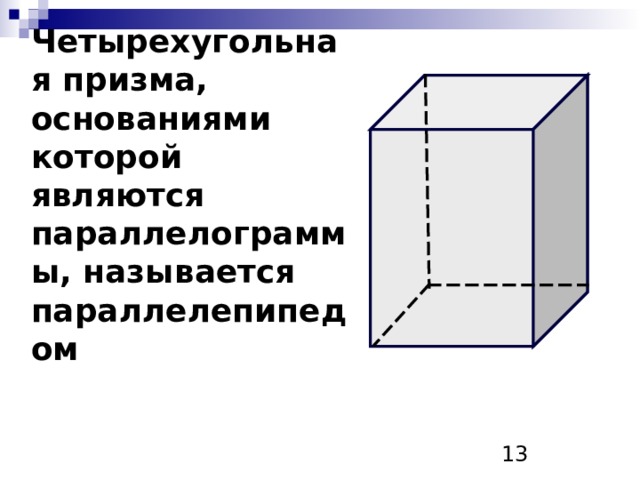
Четырехугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом

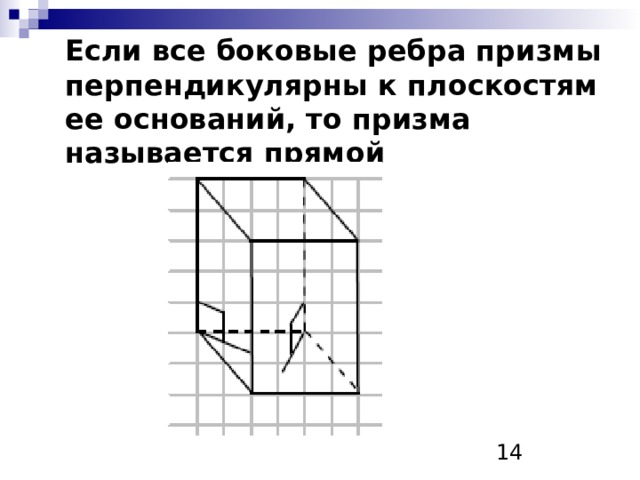
Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований, то призма называется прямой

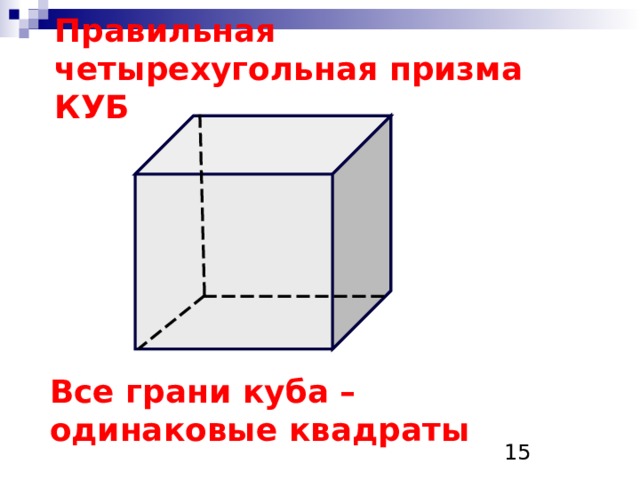
Правильная четырехугольная призма КУБ

Все грани куба – одинаковые квадраты

15

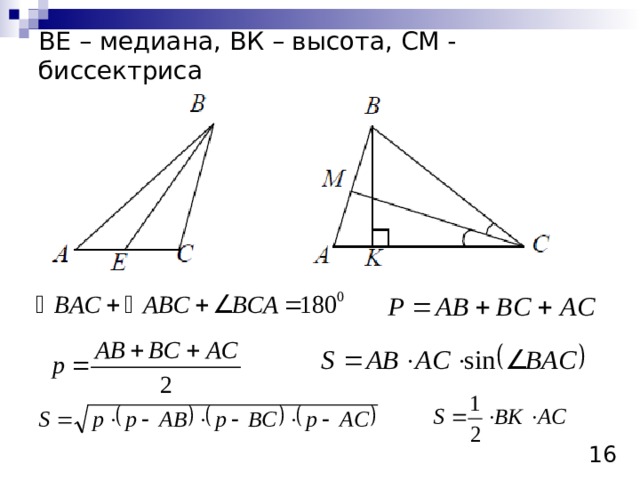
ВЕ – медиана, ВК – высота, СМ - биссектриса

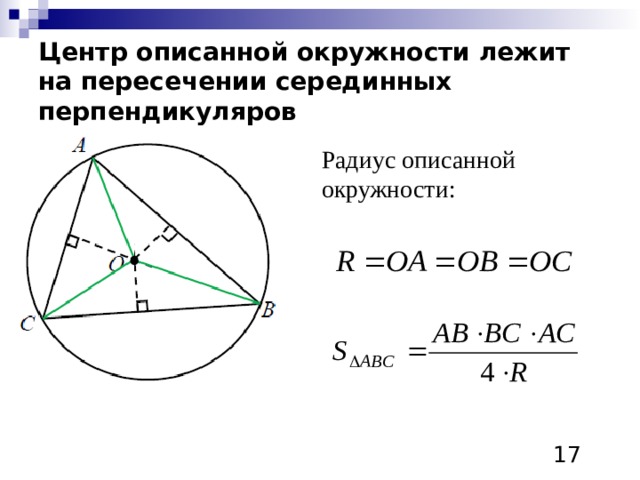
Центр описанной окружности лежит на пересечении серединных перпендикуляров

Радиус описанной окружности:

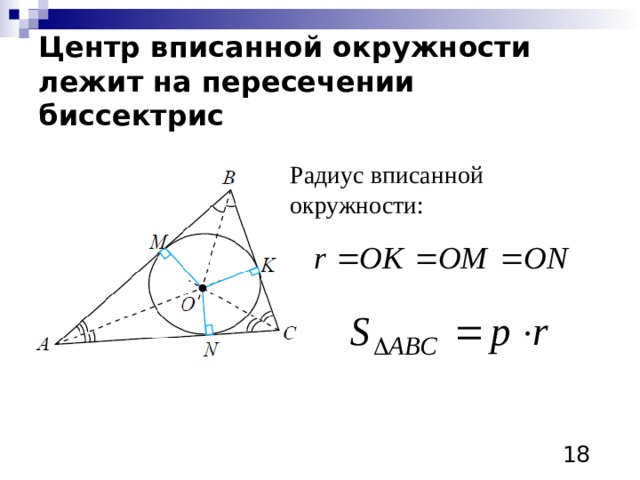
Центр вписанной окружности лежит на пересечении биссектрис

Радиус вписанной окружности:

Для правильного треугольника со стороной а:

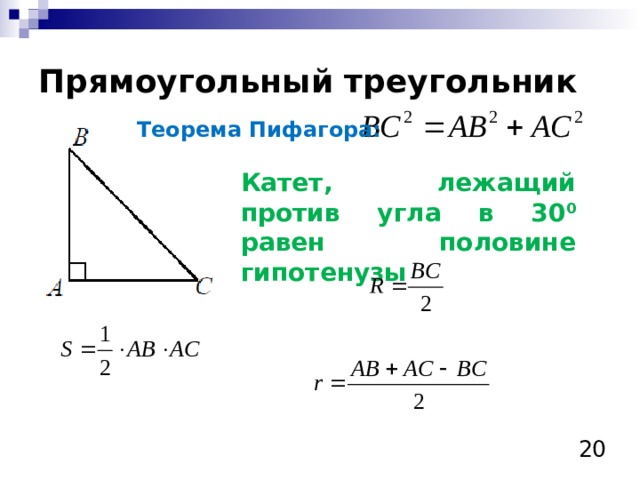
Прямоугольный треугольник

Теорема Пифагора:

Катет, лежащий против угла в 30 0 равен половине гипотенузы

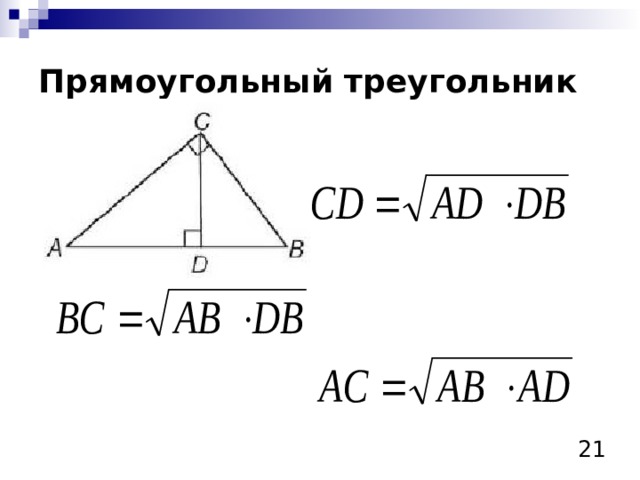
Прямоугольный треугольник

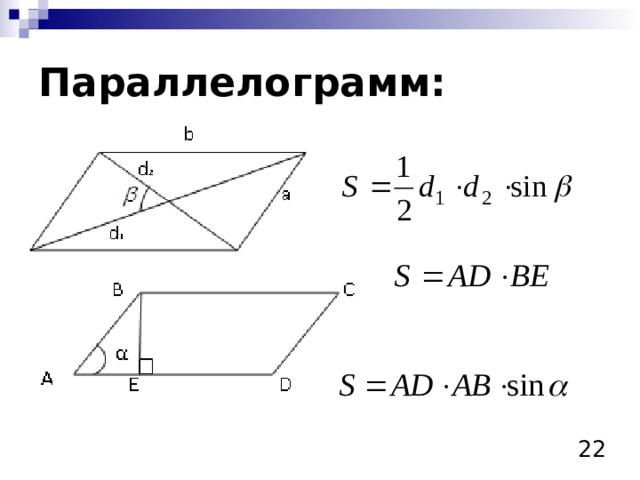
Параллелограмм:

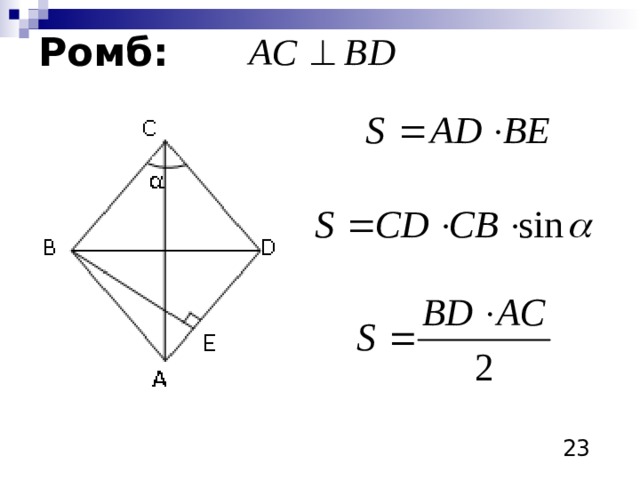
Ромб:

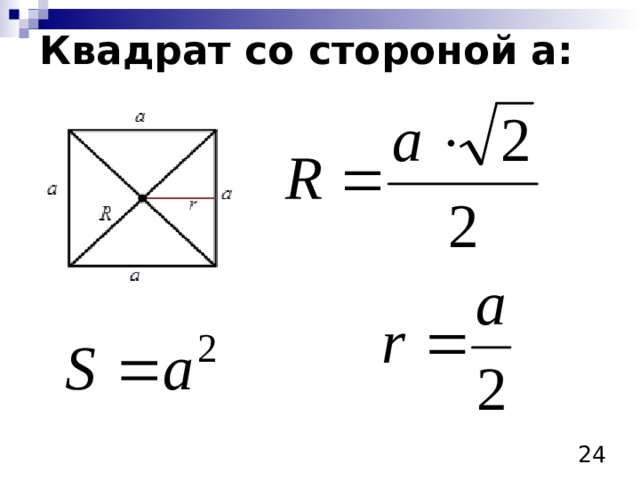
Квадрат со стороной а:

Пример 1

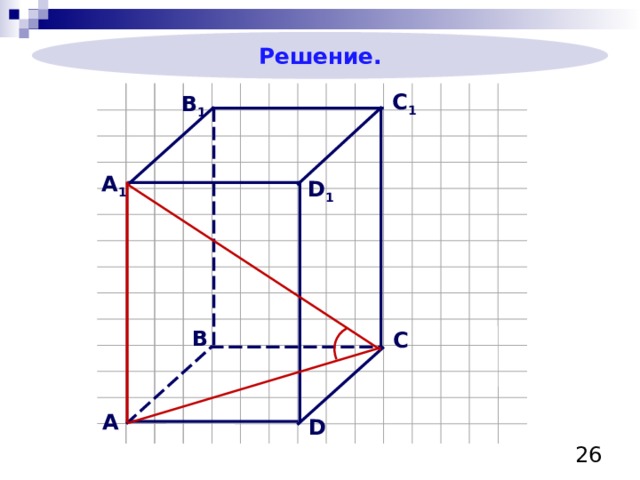
Решение.

С 1

В 1

А 1

D 1

В

С

А

D

26

Ответ: высота призмы равна 10.

26

Пример 2

26

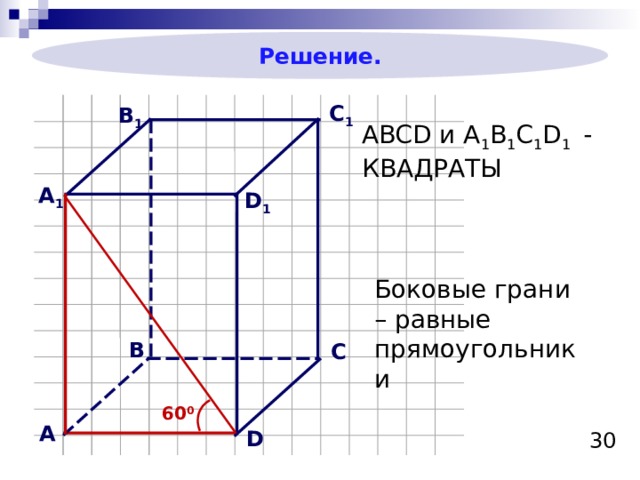
Решение.

С 1

В 1

ABCD и A 1 B 1 C 1 D 1 - КВАДРАТЫ

А 1

D 1

Боковые грани – равные прямоугольники

В

С

60 0

А

D

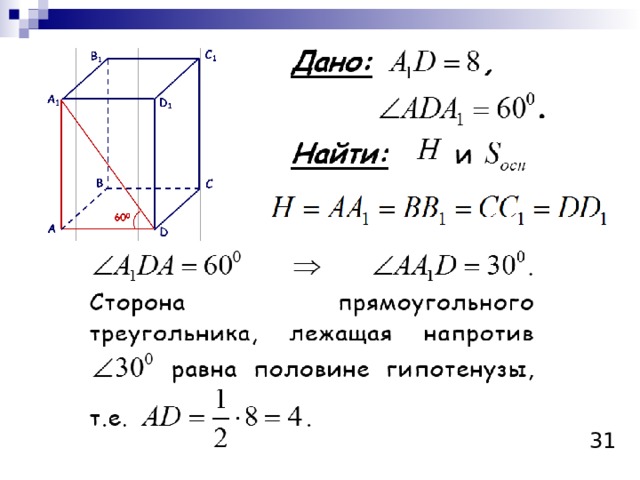
30

Ответ: площадь основания равна 16, а

высота -

30

Пример 3

Найти площадь диагонального сечения прямоугольного параллелепипеда, высота которого равна 12, а стороны основания – 8 и 6.

Решение.

С 1

В 1

А 1

D 1

В

С

А

D

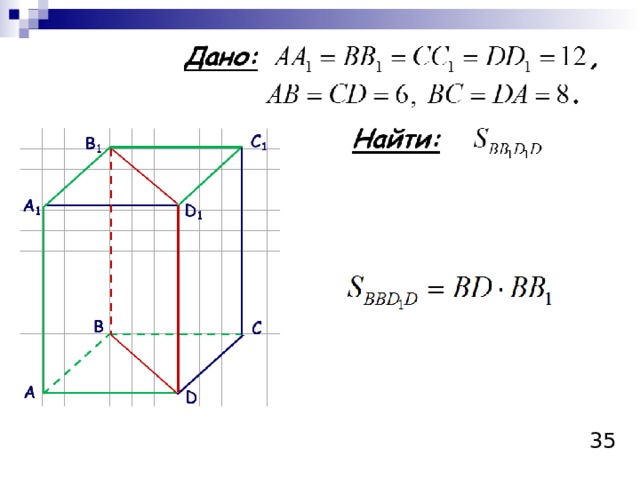
Окончательно имеем:

Ответ: площадь диагонального сечения прямоугольного параллелепипеда, высота которого равна 12, а стороны основания – 8 и 6, равна 120ед 2 .

Пример 4

Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ параллелепипеда

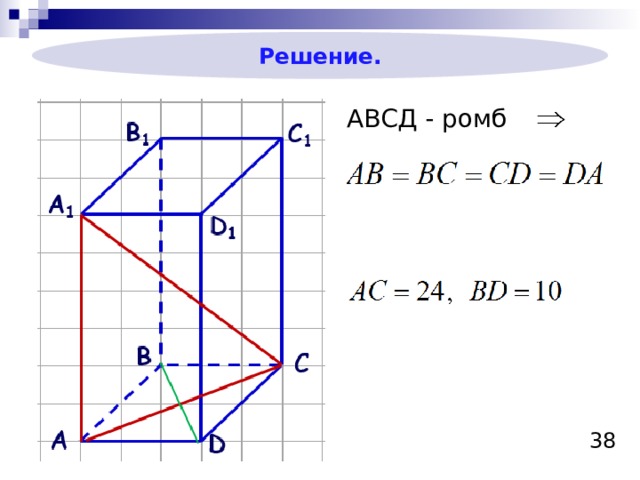
Решение.

АВСД - ромб

Ответ: большая диагональ параллелепипеда равна 26

38

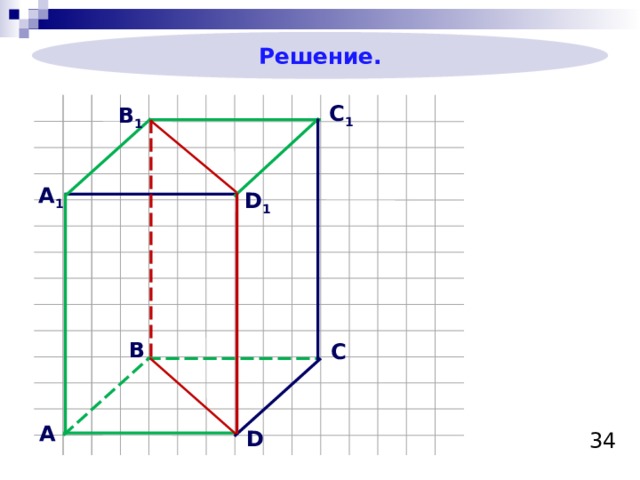
Пример 5

Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую вершину верхнего основания.

38

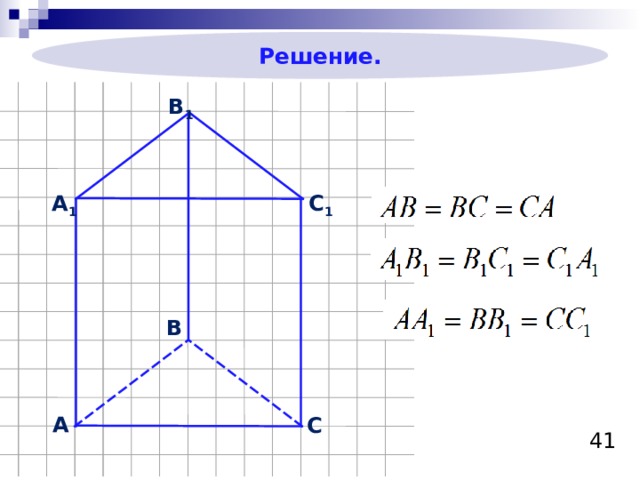
Решение.

В 1

А 1

С 1

В

А

С

38

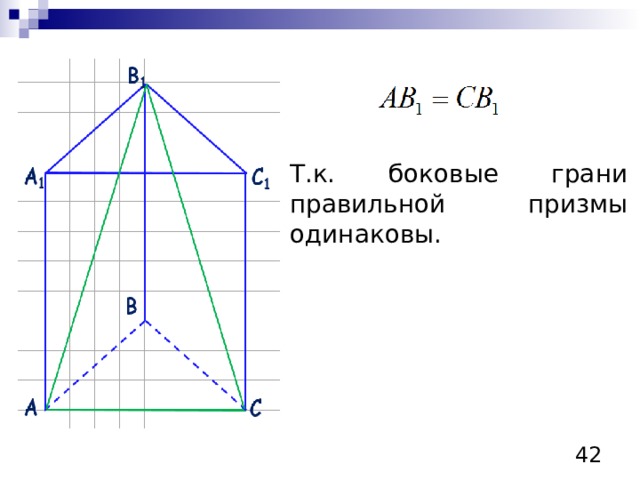
Т.к. боковые грани правильной призмы одинаковы.

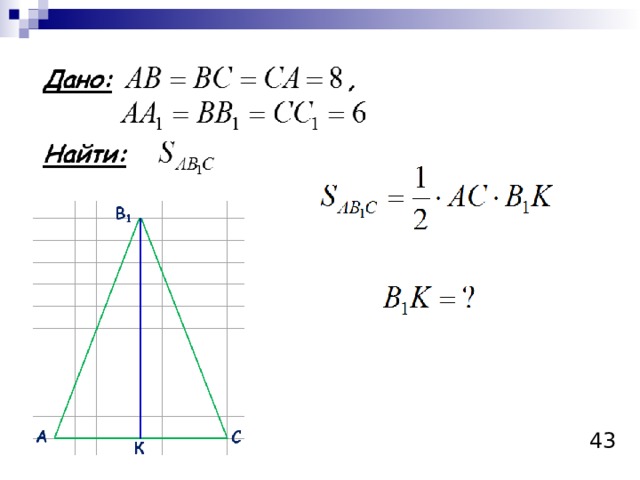
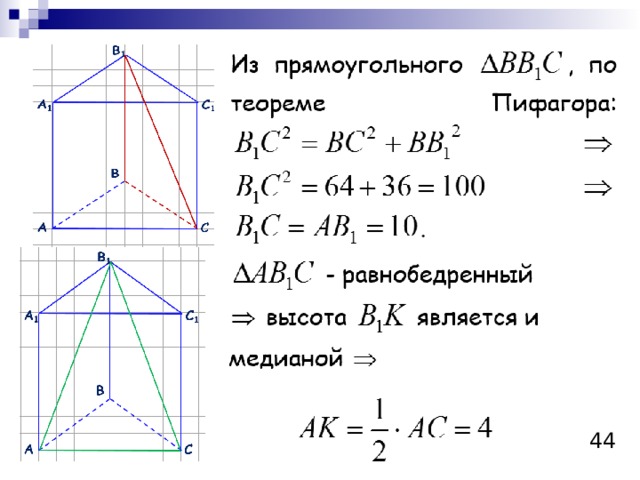
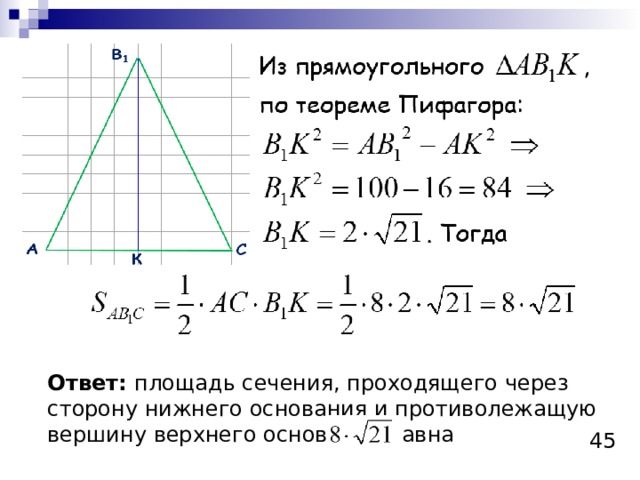
Ответ: площадь сечения, проходящего через сторону нижнего основания и противолежащую вершину верхнего основания равна

Боковая и полная поверхность призмы

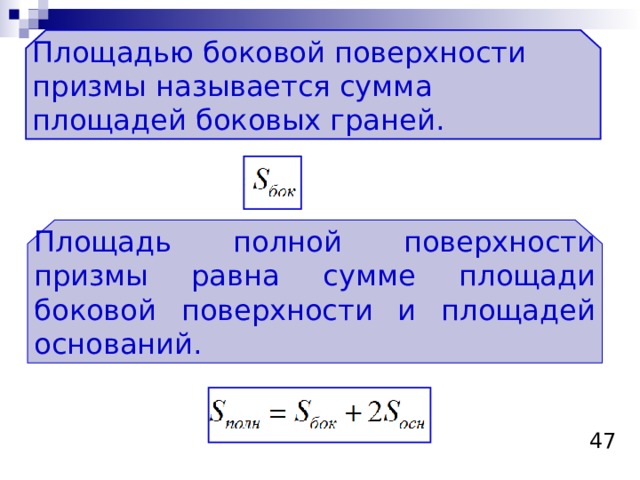
Площадью боковой поверхности призмы называется сумма площадей боковых граней.

Площадь полной поверхности призмы равна сумме площади боковой поверхности и площадей оснований.

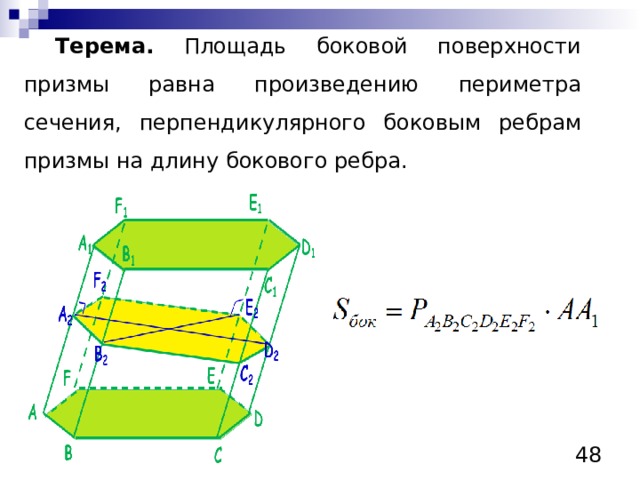
Терема. Площадь боковой поверхности призмы равна произведению периметра сечения, перпендикулярного боковым ребрам призмы на длину бокового ребра.

47

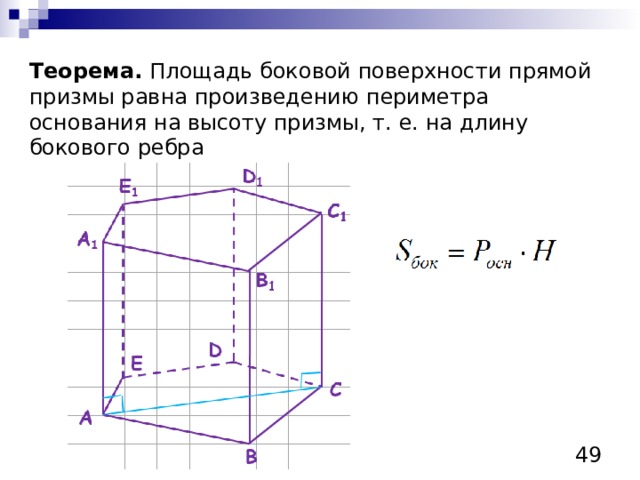
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра

47

Пример 6

47

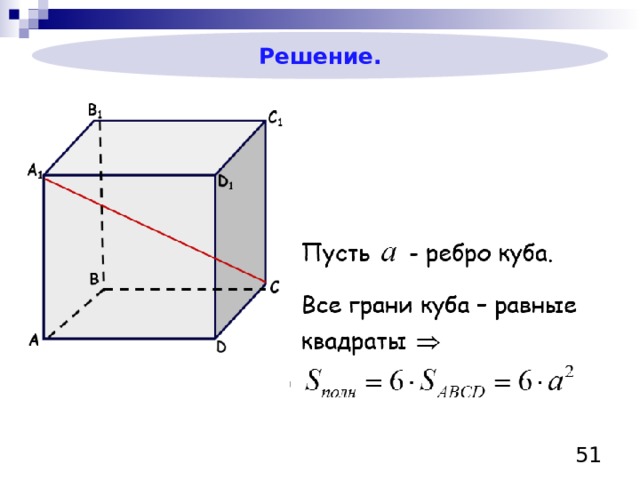
Решение.

47

Пример 7

Основание прямоугольного параллелепипеда – квадрат со стороной равной 4. Диагональ параллелепипеда, составляет с плоскостью основания угол 60°. Найти площадь боковой поверхности параллелепипеда

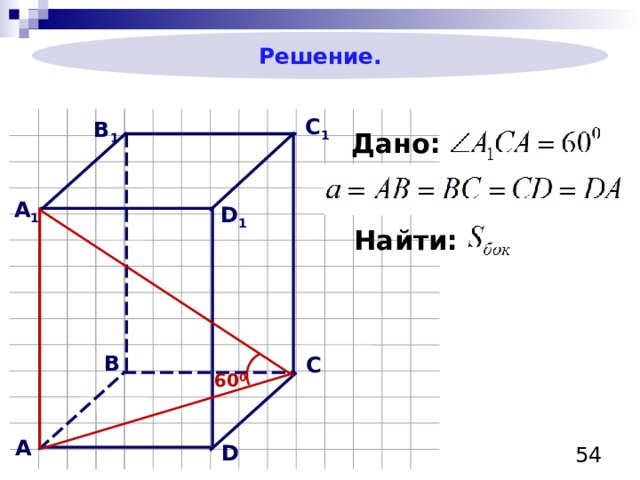
Решение.

С 1

В 1

Дано:

А 1

D 1

Найти:

В

С

60 0

А

D

Объем призмы

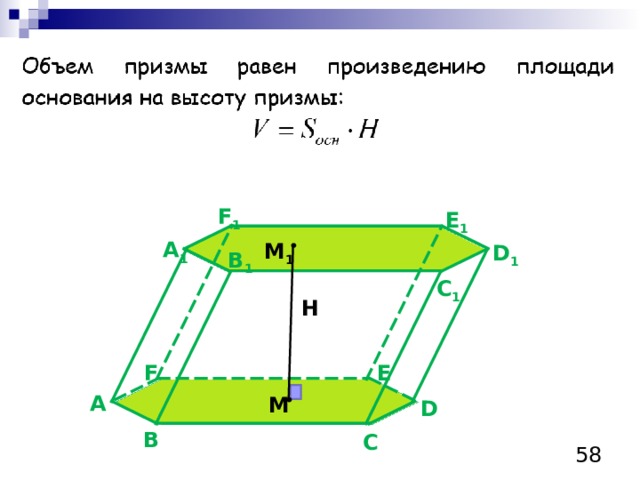
F 1

E 1

A 1

М 1

D 1

B 1

C 1

H

E

F

A

М

D

B

C

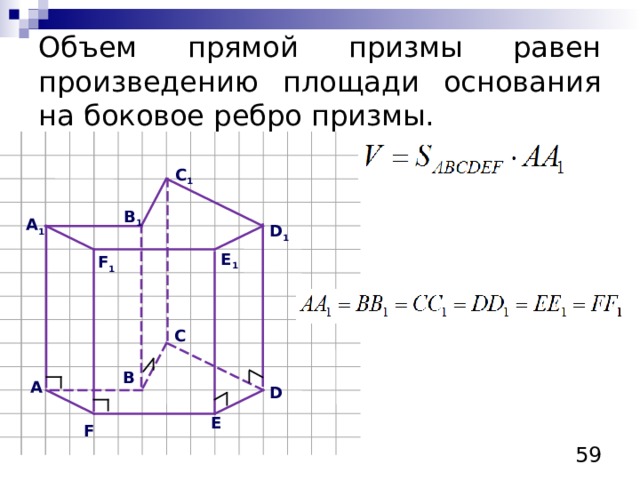
Объем прямой призмы равен произведению площади основания на боковое ребро призмы.

C 1

B 1

A 1

D 1

E 1

F 1

C

B

A

D

E

F

58

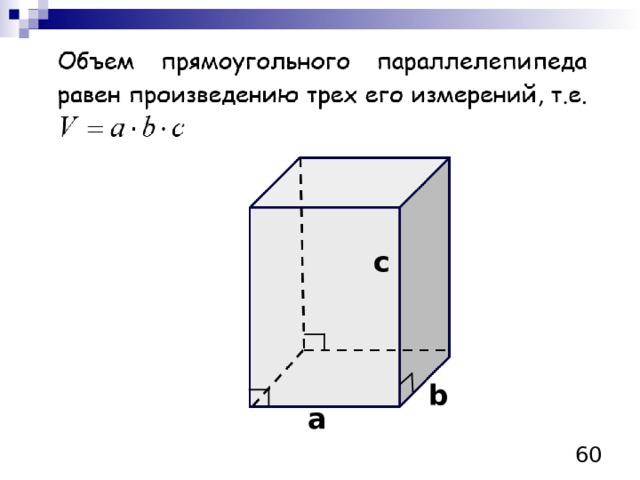
c

b

а

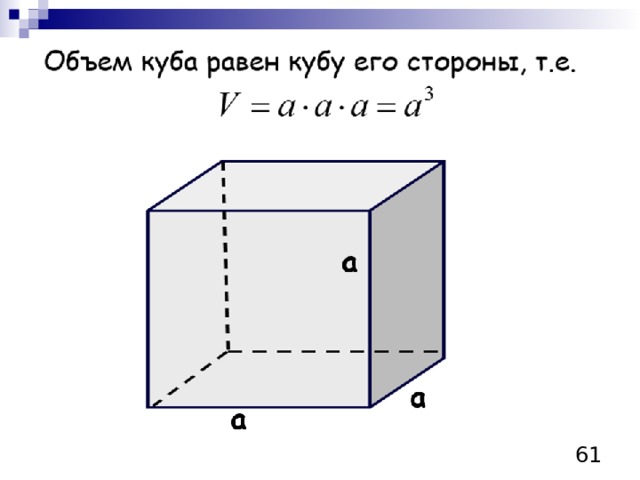
60

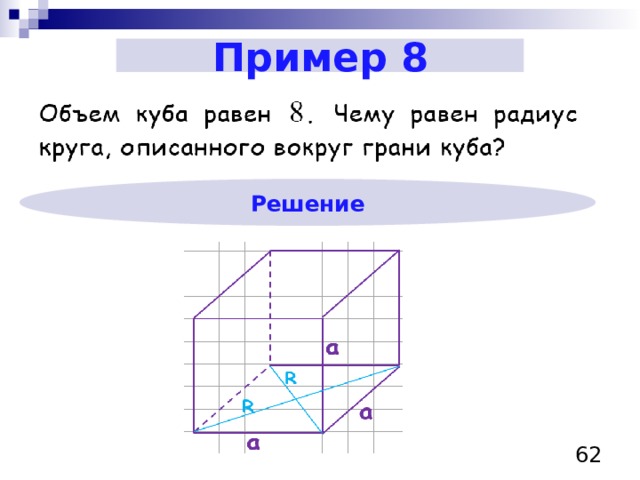
Пример 8

Решение

60

Радиус описанной окружности около квадрата:

Радиус описанной окружности около грани куба равен

Пример 9

63

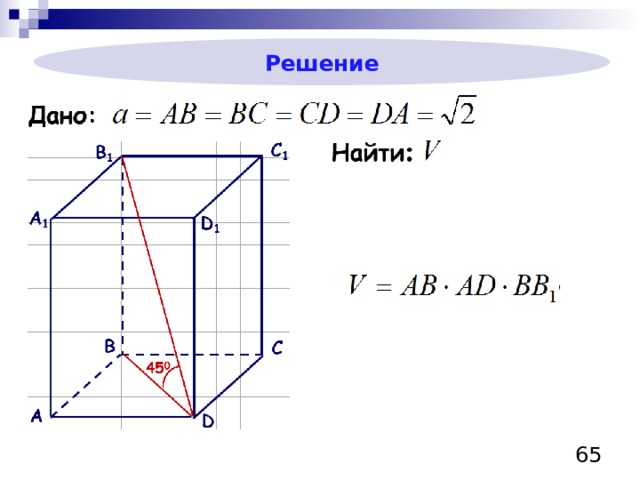
Решение

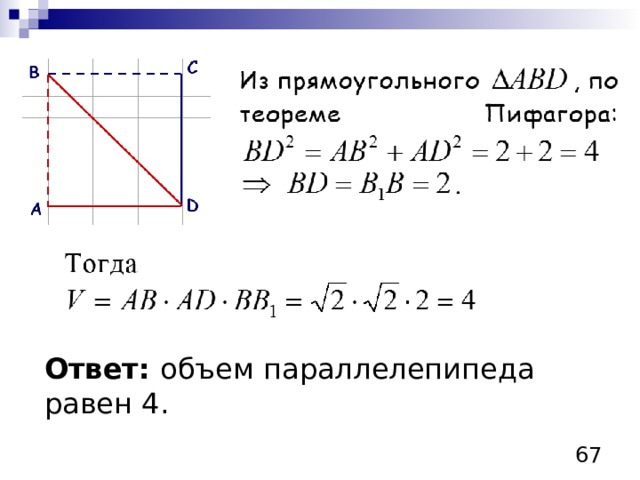
Ответ: объем параллелепипеда равен 4.