Стереометриянын аксомалары

Тема : Стереометриянын негизги т\ш\н\ктър\ жана аксиомалары

Сабактын максаты:

А) Балдарга геометриянын бир бъл\г\ болгон стереометрия боюнча жана анын негизги аксиомаларын т\ш\нд\р\\ .

Б) Маселелерди иштъъ менен ъз алдынча эмгектене бил\\гъ,сабакка болгон кызыгуусун арттыруу менен активд\\л\г\н к\чът\\гъ,тактыкка,тууралыкка,сулуулукка чакыруу менен негиздей жана далилдей бил\\гъ тарбиялоо.

В) Билимди системалдаштыруу жана теориялык материалдын канчалык деёгээлде ъздъшт\р\лгънд\г\н текшер\\.Негизги эреже, теорема , аксиома формулаларды пайдаланып маселелерди чыгаруу .

Г) Логикалык ойлоосун к\чът\\,кыска жана ыёгайлуу жолдорду табуу, негиздей жана далилдей бил\\ , эске тутуу жана оозеки,бат эсептъъ жъндъмд\\л\ктър\н, ык машыгууларын, билим билгичтик кънд\мдър\н калыптандыруу.

Сабактын тиби: салттуу

Сабактын методу : Жалпылоо,салыштыруу,суроо-жооп, кайталоо, текшер\\,изден\\ч\л\к, кърсътмъл\\л\к, анализ, синтез, инновациялык методдор.

Сабактын жабдылышы: Формулалар , плакаттар .

Сабактын ж\р\ш\: уюштуруу моменти:

1.Аудиторияны сабакка даярдоо(бор,тряпка,таблица ж.б.)

2.Студенттерди сабакка даярдоо(катышуусун къзъмълдъъ)

А) математикалык кызыктуу , жеёилирээк суроолорду бер\\ менен математикалык жъндъм\н ойготуу.

3.Таяныч билимдерди актуалдаштыруу:

1.Геометрия канча бъл\ктън турат?

2.Планиметрияда фигуралар каерде жайланышат?

3.Кандай фигуралар менен таанышсыёар? ж.б.

4.Жаёы тема баяны

Стеометриянын аксиомалары

Стереометрия - бул геометриянын мейкиндиктеги фигураларын \йрънъ турган бъл\м\. Стереометрияда геометриялык фигуралардын касиеттери планиметриядагы сыяктуу эле тиешел\ теоремаларды далилдъъ жолу менен аныкталат. Мында аксиомалар менен туюнтулуучу негизги геометриялык фигуралардын касиеттери баштапкылардан болуп эсептелет. Мейкиндиктеги негизги фигуралар болуп чекит, т\з сызык болуп эсептелет .

Тегиздикти биз столдун \ст\нк\ тегиз бети катарында элестетебиз

Тегиздиктер α, β, γ ,… грек тамгалары менен белгиленет.

Жаёы геометриялык т\спълд\(образды)- тегиздикти киргиз\\ аксиомалардын системасын кеёейт\\гъ мажбур кылат. Ошондуктан , биз мейкиндикте тегиздиктеридн негизги касиеттерин туюнтуучу аксиомалардын С группасын киргизебиз . Бул группа тъмънк\дъй \ч аксиомадан турат :

С₁: Кандай гана тегиздик болбосун ушул тегиздикте жаткан чекиттер жана анда жатпаган чекиттер бар .

С₂: Эгер ар т\рд\\ эки тегиздик жалпы чекитке ээ болушса , анда алар ушул чекит аркылуу ъткън т\з сызык боюнча кесилишет.

С₃: Эгер ар т\рд\\ эки т\з сызык жалпы чекитке ээ болсо , анда алар аркылуу тегиздик ж\рг\з\\г\ болот , бирок бирди гана.

Бул эгер ар т\рд\\ эки a жана b т\з сызыгы С жалпы чекиттке ээ болсо , анда a жана b т\з сызыктарын камтыган γ тегиздиги болорун билдирет . Мындай касиетке ээ болгон тегиздик жалгыз гана.

Эскерт\\. Планиметрияда бизде бир тегиздик болгон жана анда бардык биз караган фигуралар жайланышкан болуучу . Стереометрияда тегиздиктер къп,чексиз къп болот. Ушуга байланыштуу планиметриянын кайсы бир аксиомаларынын айтылыштары стреометринын аксиомалары катарында тактоолорду талап кылат.

4-аксиома: Тегиздикте жаткан т\з сызык ушул тегиздикти эки жарым тегиздикке бълът .

5-аксиома : Тегиздикте жаткан жарым т\з сызыктан анын берилген жарым тегиздигине 180⁰ тан кичине градустук чени менен берилген бурчту ченеп коюуга болот жана бирди гана.

6-аксиома : Кандай гана \ч бурчтук болбосун берилген тегиздиктин жарым т\з сызыгына карата анын кърсът\лгън жарым тегиздигинде ага барабар \ч бурчтук болот.

7-аксиома : Тегиздикте берилген т\з сызыкта жатпаган чекит аркылуу ага параллель бол

Берилген т\з сызык жана берилген чекит аркылуу ъткън тегиздиктин бар экени

Т₁ : Т\з сызык жана анда жатпаган чекит аркылуу тегиздик ж\рг\з\\гъ болот, бирок бирди гана.

Далилдъъ: АВ – берилген т\з сызык жана С – т\з сызыкта жатпаган чекит болсун .

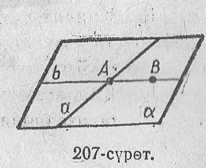
А жана С чекиттери аркылуу т\з сызык ж\рг\зъб\з (1-аксиома) . АВ жана АС т\з сызыктары ар т\рд\\ , себеби С чекити АВ т\з сызыгында жатпайт . АВ жана АС т\з сызыктары аркылуу α тегиздигин ж\рг\зъб\з (С₃ аксиома) Ал тегиздик АВ т\з сызыгы жана С чекити аркылуу ътът.

АВ т\з сызыгы жана С чекити аркылуу ъткън α тегиздигинин жалгыз экенин далилдейбиз.

АВ т\з сызыгы жана С чекити аркылуу ът\\ч\ башка α¹ тегиздиги бар дейли . С₂ аксиомасы боюнча α жана α¹ тегиздиктери т\з сызык боюнча кесилишет . Бул т\з сызыкта А, В, С чекиттери болууга тийиш. Бирок алар бир т\з сызыкта жатышпайт . Биз карама-каршылыкка келдик . Теорема далилденди.

Сабакты бышыктоо максатында берил\\ч\ суроолор:

1. Стреометрия эмнелерди окутат?

2. Стреометриянын аксиомаларын айтып бергиле.

3. Бул аксиомалардан келип чыгуучу теоремалар кандайча айтылат?

4. Ал теорамаларды далилдегиле.

Сабакта студенттерге тъмъндъг\дъй тесттти таратып, алардын билимин текшер\\гъ болот:

1. Стреометрия деген эмне?

А) мейкиндиктеги фигуралардын касиеттерин окутуп \йрът\\ч\ геометриянын бир бъл\г\.

Б) тегиздиктеги фигуралардын касиеттерин окутуп \йрът\\ч\ геометриянын бъл\г\.

В) бул геометриянын бир т\р\

2. Теорема деген эмне ?

А) далилдъън\ талап кылбаган с\йлъм

Б) далилдъън\ талап кылган с\йлъм.

В) математикалык с\йлъм.

3. Аксиома деген эмне?

А) далилдъън\ талап кылбаган с\йлъм

Б) далилдъън\ талап кылган с\йлъм.

В) математикалык с\йлъм.

4. Стреометриянын 1 - аксиомасы:

А) Эгер ар т\рд\\ эки тегиздик жалпы чекитке ээ болушса , анда алар ушул чекит аркылуу ъткън т\з сызык боюнча кесилишет.

Б) Кандай гана тегиздик болбосун ушул тегиздикте жаткан чекиттер жана анда жатпаган чекиттер бар .

В) Эгер ар т\рд\\ эки т\з сызык жалпы чекитке ээ болсо , анда алар аркылуу тегиздик ж\рг\з\\г\ болот , бирок бирди гана.