Сценарий урока "Использование ИКТ на уроках математики по теме: «Построение графиков тригонометрических функций»."

Использование ИКТ на уроках математики по теме: «Построение графиков тригонометрических функций».

На уроках с использованием ИКТ, также как и на других уроках, учителю для успешного проведения компьютерного урока приходится решать следующие задачи: дидактическая (подготовка учебного материала урока, конкретная компьютерная программа); методическая (определить методы использования компьютера в преподавании темы, анализ результатов урока, постановка следующей учебной цели); организационная (организовать работу, избегая перегрузки учащихся и нерациональной траты времени); учебная (выработать и закрепить у учащихся знания по рассматриваемой теме, умения и навыки работы с предложенной программой).

Как показывает опыт, уроки с применением компьютерных систем не заменяют учителя, а наоборот, делают общение ученика с учителем более содержательным, индивидуальным и деятельным. Использование ЭВМ на уроках математики экономит время, повышает эффективность учебно-познавательного процесса.

Класс: 10.

Предмет: алгебра и начала анализа.

Цели урока:

Обучающая: сформировать умение и навыки построения графиков тригонометрических функций, используя преобразования графиков и основные свойства; способствовать самостоятельной деятельности учащихся.

Воспитывающая: Способствовать воспитанию у учащихся внимания, аккуратности и самостоятельности при решении задач.

Развивающая: развивать логическое мышление.

Оборудование: интерактивная доска; компьютеры; раздаточный материал; справочный материал.

Структура урока:

I. Организационный момент. Сообщение темы и цели урока. (1 мин).

II. Актуализация опорных знаний. Чтение графиков, повторение свойств тригонометрических функций с помощью программы Mathcad Professional.

1) Свойства синуса

2) Свойства косинуса

3) Свойства тангенса

4) Свойства котангенса

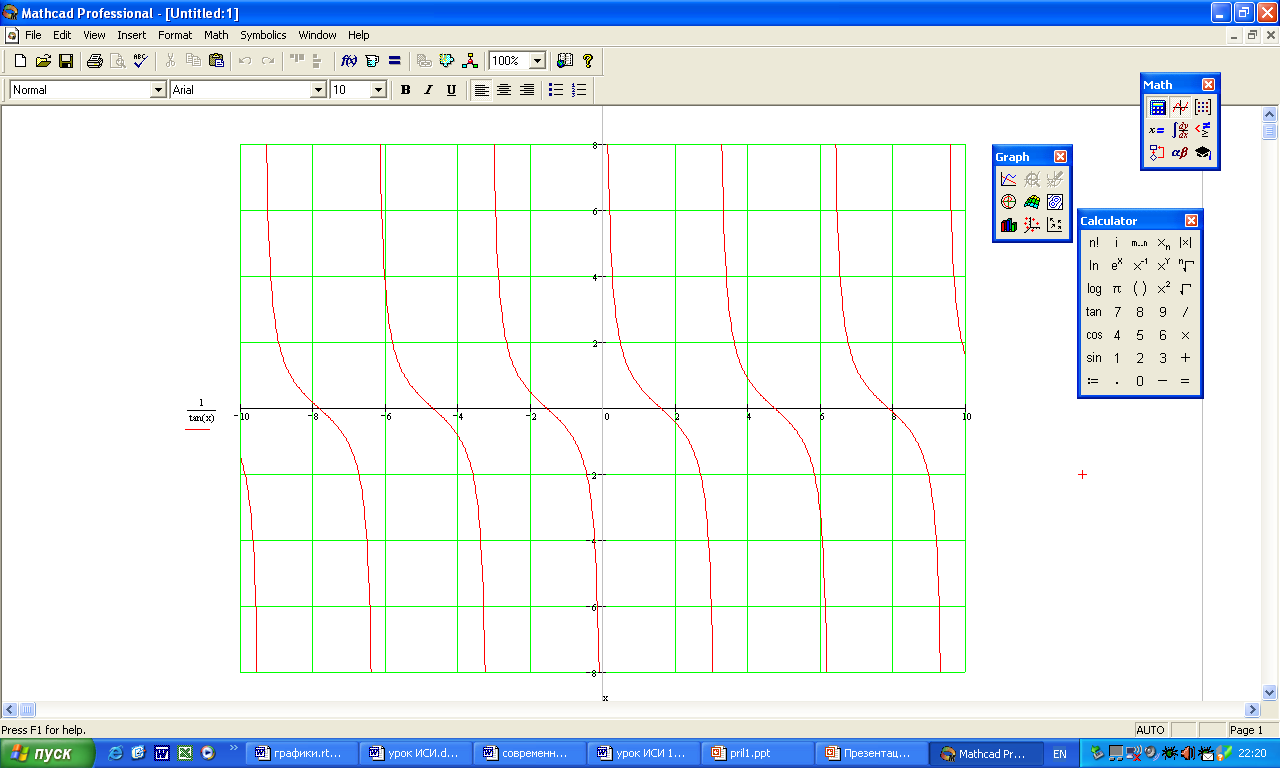
III. Практическая работа, с использованием интерактивной доски.

1) Построение графиков тригонометрических функции.

Построение графиков осуществляется учащимися у доски, а остальные учащиеся выполняют построение графиков на рабочих листах.

Графики каких функций изображены на рисунке.

IV. Разгадывание кроссворда.

1. Буква латинского алфавита.

2. Тригонометрическая функция, график которой расположен симметрично относительно начала координат.

3. Угол поворота против часовой стрелки.

4. Свойство функции.

5. 1 части прямого угла.

90

Учащиеся должны разгадать кроссворд и узнать великого математика 18 века. Включается исторический материал про Леонарда Эйлера.

К началу 18 века тригонометрия была еще недостаточно разработана: не было условных обозначений, формулы записывались словами, усваивать их было трудно, неясным был и вопрос о знаках тригонометрических функций в разных четвертях круга, под аргументом тригонометрической функции понимали только углы или дуги. Только в трудах Эйлера тригонометрия получила современный вид. Именно он стал рассматривать тригонометрическую функцию числа, т.е. под аргументом стали понимать не только дуги или градусы, но и числа. Эйлер вывел все тригонометрические формулы из нескольких основных, упорядочил вопрос о знаках тригонометрической функции в разных четвертях круга. Для обозначения тригонометрических функций он ввел символику: sin x, cos x, tg x, ctg x.

V. Выполнение самостоятельной работы.

В-1

Построить график функции и перечислить его свойства

а) _

В-2

Построить график функции и перечислить его свойства

а) _

VI. Подведение итого урока.

VII. Домашнее задание. Построить графики функций.